5 câu hỏi
Gọi S là tập hợp các số tự nhiên có hai chữ số. Chọn ngẫu nhiên đồng thời hai số từ tập hợp S. tính xác suất để hai số được chọn có chữ số hàng đơn vị giống nhau.
\(\frac{8}{{89}}.\)
\(\frac{{81}}{{89}}.\)
\(\frac{{36}}{{89}}.\)
\(\frac{{53}}{{89}}.\)
Số nghiệm của phương trình \({\log _3}x = {\log _2}\left( {1 + \sqrt x } \right)\) là
0.
3.
1.
2.
Cho hàm số y = ax3 + bx2 + cx + d có đồ thị như hình vẽ. Tìm mệnh đề đúng.
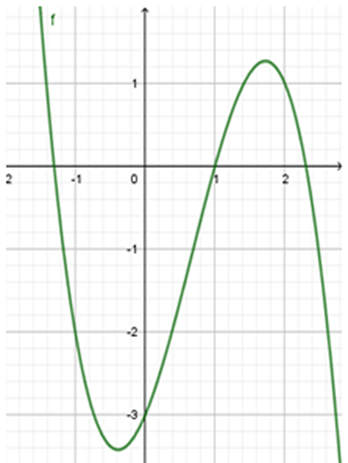
a < 0, b > 0, c > 0, d < 0.
a < 0, b < 0, c > 0, d < 0.
a > 0, b > 0, c > 0, d < 0.
a < 0, b > 0, c < 0, d < 0.
Trong không gian Oxyz, mặt phẳng (Oxz) có phương trình là
z = 0.
x + y + z = 0.
y = 0.
x = 0.
Cho a, b, c là ba số thực dương và khác 1. Đồ thị các hàm số y = ax, y = logbx, y = logcx được cho trong hình dưới đây:
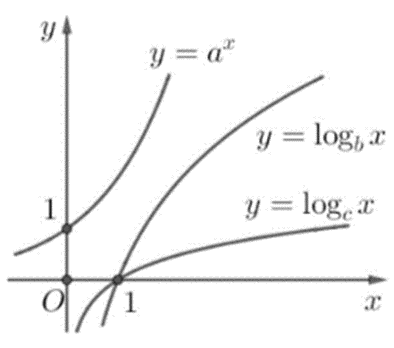
Mệnh đề nào dưới đây đúng?
a < b < c.
c < b < a.
b < c < a.
b < a < c.