10000 câu trắc nghiệm tổng hợp môn Toán 2025 mới nhất (có đáp án) - Phần 39
72 câu hỏi
Trong mặt phẳng Oxy, cho điểm M(4;4) và đường thắng d: 3x – y + 2 = 0.Tìm tọa độ điểm H là hình chiếu vuông góc của M trên d.
Trong mặt phẳng Oxy, cho điểm M(4;4) và đường thắng d: 3x – y + 2 = 0.Tìm tọa độ điểm N đối xứng với M qua d.
Cho đường thẳng d: x - 2y + 4 = 0 và điểm A(4;1).Tìm toạ độ hình chiếu vuông góc của A xuống d.
Cho đường thẳng d: x - 2y + 4 = 0 và điểm A(4;1).Tìm toạ độ B đối xứng với A qua d.
Trong mặt phẳng toạ độ, cho các điểm A(0;2); B(1;1); C(-1;-2). Các điểm A'; B'; C' lần lượt chia các đoạn BC, CA, AB theo các tỉ số 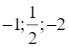 . Các mệnh đề đúng hay sai?
. Các mệnh đề đúng hay sai?
a) 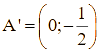
b) 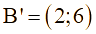
c) 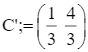
d) Ba điểm A'; B'; C' thẳng hàng
Trong mặt phẳng toạ độ Oxy, cho tam giác DEF có D(1;-1), E(2;1), F(3;5). Khi đó các mệnh đề sau đúng hay sai:
(a) Đường thẳng vuông góc với đường thẳng EF nhận ![]() là một vec tơ chỉ phương
là một vec tơ chỉ phương
(b) Phương trình đường cao kẻ từ D là: x + y = 0.
(c) Gọi I là trung điểm của DF. Toạ độ của điểm I là (2;2).
(d) Đường trung tuyến kẻ từ E có phương trình là: x – 2 = 0.
Trong một vòng thi Olympic Toán gồm có 15 câu hỏi với thể lệ như sau: Mỗi câu trả lời đúng thi sinh được 5 điểm, mỗi câu trả lời sai thí sinh bị trừ 2 điểm. Bạn Bảo sau khi trả lời tất cả các câu hỏi của vòng thi này và đạt được 40 điểm. Hỏi bạn Bảo đã trả lời đúng bao nhiêu câu?
Từ 101 đến 160 có bao nhiêu số không chia hết cho 9?
1 can đựng được 9 lít dầu nặng 9,3kg can rỗng nặng 1,65kg. Hỏi mỗi lít dầu cân nặng bao nhiêu kg?
Tìm ƯCLN rồi tìm tập hợp ước chung của 80 và 150.
Vào tháng 5, giá niêm yết của một chiếc ti vi 42 inch tại một siêu thị điện máy là 8000000 đồng. Đến tháng 8, siêu thị giảm giá 5% cho mỗi chiếc ti vi. Sang tháng 9, siêu thị lại giảm giá thêm một lần nữa, lúc này giá của một chiếc ti vi 42 inch chỉ còn 6840000 đồng. Hỏi tháng 9, siêu thị đã giảm giá bao nhiêu phần trăm cho một chiếc ti vi so với tháng 8?
Tìm phân số bằng phân số ![]() , biết rằng tổng của tử và mẫu của nó bằng 900.
, biết rằng tổng của tử và mẫu của nó bằng 900.
Viết 4,25 dưới dạng hỗn số
Viết phương trình tổng quát của đường thẳng đi qua điểm I(-1;2) và M(0;4).
Phân tích số 2024 thành tổng giá trị các chữ số của nó.
Tìm x biết: 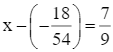 .
.
Tìm x biết: 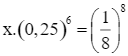 .
.
Tìm x biết x chia hết cho 12 và 13 < x < 75.
Giải phương trình: ![]() .
.
Cho x, y > 0 thỏa mãn x + 2y ≥ 5. Tìm GTNN của 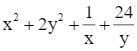 .
.
Tìm x, y, z biết: 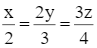 và xyz = –108.
và xyz = –108.
Tìm x, y biết: 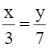 và x2 + y2 = 58.
và x2 + y2 = 58.
Tìm x, y biết: 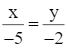 và xy = 160.
và xy = 160.
Tìm x, y biết: 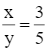 và 2x – y = 11.
và 2x – y = 11.
Cho x : y : z = 2 : 3 : 5 và x − y + z = − 12. Tìm x, y, z?
Tìm giá trị nhỏ nhất của biểu thức: A = x2 + 2y2 + 2xy − 2x − 6y + 2025.
Tìm x, y nguyên thỏa mãn x2 + 5y2 – 4xy – 4y + 3 = 0.
Phân tích đa thức thành nhân tử: x2 + 6x – 3(x + 6)
Cho x2 + y2 – xy = 4. Tìm GTLN và GTNN của P = x2 + y2.
Cho x2 - 2(m - 1)x – m = 0. Chứng minh phương trình luôn luôn có 2 nghiệm x1, x2 với mọi m.
Phân tích đa thức thành nhân tử: x2 – x – 2020.2021
Cho 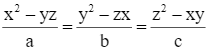 . Chứng minh rằng:
. Chứng minh rằng:
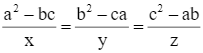 .
.
Tìm nghiệm của phương trình: x5 + x + 1 = 0
Giải phương trình: x5 + x4 + x3 + x2 + x + 1 = 0.
Chứng minh phương trình: x7 + 3x5 – 1 = 0 có ít nhất một nghiệm.
Tìm x biết: 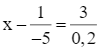 .
.
Khai triển: x13 – x23
Tìm x biết: 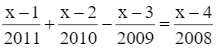 .
.
Tìm x biết: 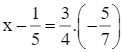 .
.
Cho phương trình x2 – (2m – 1)x + 6 – 4m2 = 0.Tìm m để phương trình có 2 nghiệm trái dấu.
Cho phương trình x2 – (2m – 1)x + 6 – 4m2 = 0.Tìm m để phương trình có 2 nghiệm trái dấu sao cho x12 + x1 + x1x2 = 6x22 + 2x2.
Tìm x thỏa mãn: 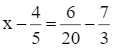 .
.
Xác định parabol y = ax2 + bx + c (a khác 0) biết đường thẳng y = −2 cắt (P) tại hai điểm có hoành độ −1 và 3, đồng thời hàm số có giá trị lớn nhất bằng 2.
Tìm x biết: 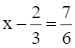 .
.
Tìm các cặp số nguyên x, y biết xy + 7x - 3y – 26 = 0
Một hộp kín hình lập phương cạnh 10 cm. Tính thể tích chiếc hộp đó.
Một khu vườn hình chữ nhật có chiều dài 30 m, chiều rộng 20 m. Ở giữa khu vườn người ta xây một bồn hoa hình thoi có độ dài hai đường chéo là 4,5 m và 3 m. Tính diện tích phần còn lại của khu vườn.
Một khúc gỗ tròn hình trụ cần xẻ thành một chiếc xà hình trụ có đường kính đáy là 4 cm và dài 5 m. Tính thể tích phần gỗ cần sử dụng để làm chiếc xà.
Một khúc sông từ bến A đến bến B dài 45 km. Một ca nô xuất phát từ bến A với vận tốc 15 km/giờ. Sau bao lâu thì ca nô đó đi đến điểm B.
Một người đi xe đạp từ A đến B cách nhau 24 km. Một giờ sau, một người đi xe máy từ A đến B và đến trước người đi xe đạp 20 phút. Tính vận tốc của mỗi người, biết vận tốc xe máy gấp 3 lần vận tốc của xe đạp.
Một người gửi ngân hàng 150 triệu đồng với lãi suất 0,6%/tháng. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được nhập làm vốn ban đầu để tính lãi cho tháng tiếp theo. Hỏi sau ít nhất bao nhiêu tháng, người đó được lĩnh số tiền không ít hơn 160 triệu đồng (cả vốn ban đầu và lãi), biết rằng trong suốt thời gian gửi tiền người đó không rút tiền và lãi suất không thay đổi?.
Một người nông dân có 15 triệu đồng, anh ta mua một con bò giá 15 triệu, rồi bán đi với giá 17 triệu, sau đó mua lại giá 20 triệu rồi lại bán đi với giá 19 triệu. Người bán bò lãi bao nhiêu tiền?.
Nếu hôm nay là thứ hai, thì 63 ngày sau sẽ là thứ mấy trong tuần?
Chọn khẳng định đúng trong các khẳng định dưới đây:
Những số chia hết cho 9 thì chia hết cho 3.
Những số chia hết cho 3 thì chia hết cho 9.
Những số có chữ số tận cùng là 3 thì chia hết cho 3.
Những số có chữ số tận cùng là 3 hoặc 9 thì chia hết cho 9.
Qua hai đường thẳng cắt nhau có thể tạo được bao nhiêu mặt phẳng?
0.
1.
2.
3.
Số bé nhất có 6 chữ số mà tổng các chữ số bằng 12 là bao nhiêu?
Số lớn nhất có 2 chữ số lớn gấp 7 lần tổng các chữ số của số đó là bao nhiêu?
So sánh P và P2 với 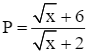 .
.
Cho phương trình ![]() . Tập hợp các số thực m để có nghiệm là nửa khoảng [a; b). Tính a + b.
. Tập hợp các số thực m để có nghiệm là nửa khoảng [a; b). Tính a + b.
Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M(4; 1) lên đường thẳng (d): x – 2y + 4 = 0.
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh SA vuông góc với mặt phẳng đáy và SA = 2a. Gọi M là trung điểm của SC. Tính cosin của góc α là góc giữa đường thẳng BM và mặt phẳng (ABC).
Trong không gian với hệ tọa độ Oxyz, cho các điểm A(2; −1; 0) , B(3; −3; −1) và mặt phẳng (P): x + y + z − 3 = 0. Tìm tọa độ giao điểm M của đường thẳng AB với mặt phẳng (P).
Một nhà bè nuôi cá lồng, năm trước thu được 1 340 kg cá. Năm nay thu được sản lượng cá gấp hai lần năm trước. Tính sản lượng cá đã thu được trong năm nay?
Một chất điểm chuyển động có phương trình vận tốc là ![]() (m/s) với t là thời gian chuyển động (giây). Hỏi trong khoảng thời gian 10 giây đầu tiên, vận tốc nhỏ nhất của chất điểm là bao nhiêu?
(m/s) với t là thời gian chuyển động (giây). Hỏi trong khoảng thời gian 10 giây đầu tiên, vận tốc nhỏ nhất của chất điểm là bao nhiêu?
Trong không gian hệt tọa độ Oxyz, cho A(1; −1; 2) và B(3; 2; −3). Tính độ dài đoạn thẳng AB.
Trong mặt phẳng tọa độ Oxyz cho các điểm A(2; 0; 2), B(0; 2; 0), C(1; 0; 3). Gọi M là điểm trong không gian thoải mãn MA2 + MC2 = MB2. Tính MP với P(3; 2; −5).
Một trường học có hai máy in A và B hoạt động độc lập. Trong 24 giờ hoạt động, xác suất để máy A và máy B gặp lỗi kĩ thuật tương ứng là 0,08 và 0,12. Xác suất để trong 24 giờ hoạt động có nhiều nhất một máy gặp lỗi kĩ thuật là bao nhiêu?
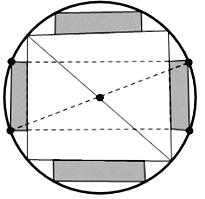
Từ một khúc gỗ hình trụ có đường kính 40cm, cần xả thành một chiếc xà có tiết diện ngang là hình vuông và bốn miếng phụ được tô màu xám như hình vẽ. Tìm chiều rộng x của miếng phụ để diện tích sử dụng theo tiết diện ngang là lớn nhất.
Viết số 2024 thành tổng giá trị các chữ số của nó
Cho hai số thực dương thỏa mãn . Khẳng định nào sau đây là đúng?
A. 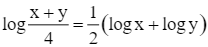 .
.
B. 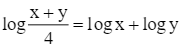 .
.
C. 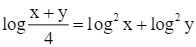 .
.
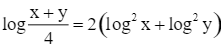
Với các số thực ko âm x và y thỏa mãn x2 + y2 = 4, Tìm GTNN của biểu thức P = x + 2y.
So sánh m2 và m nếu 0 < m < 1








