10000 câu trắc nghiệm tổng hợp môn Toán 2025 mới nhất (có đáp án) - Phần 36
100 câu hỏi
Biết 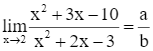 . Tính ab?
. Tính ab?
Biết rằng giá niêm yết của một chiếc máy tính thương hiệu Dell trong một cửa hàng là 20000000 đồng. Nhân dịp ngày lễ, cửa hàng giảm giá 5% và giảm giá thêm 2% nếu khách hàng thanh toán bằng tiền mặt. Hỏi khi thanh toán bằng tiền mặt, khách hàng phải trả bao nhiêu tiền cho chiếc máy tính đó?
Cho hình vẽ:
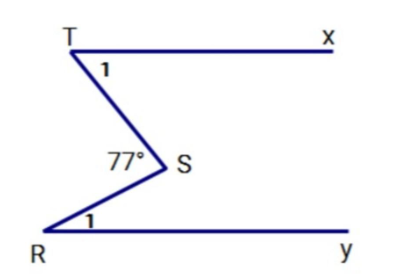
Biết Tx // Ry; ![]() . Tính
. Tính ![]() ?
?
Trong các số sau số nào là bội của 26?
-52
-13
-2
13
Có bao nhiêu số tự nhiên vừa là bội của 45 vừa là ước của 300?
Tìm x và y biết: 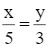 và x2 – y2 = 1600
và x2 – y2 = 1600
Các công nhân của một nhà máy xếp 24150 hộp bánh vào các thùng mỗi thùng 30 hộp bánh. Những thùng bánh này sau đó được phân phối đều cho 23 đại lý. Hỏi mỗi đại lý nhận được bao nhiêu thùng bánh?
Trong tam giác có mấy loại đường, tính chất của từng loại đường, ghi ra bằng kí hiệu.
Trong khoảng từ 1 đến 20, các số chia 7 dư 1 là số nào?
Các cách chứng minh tia phân giác.
Cách đổi từ vectơ chỉ phương sang vectơ pháp tuyến
Cách tính diện tích hình tròn.
Cách vẽ tam giác cân bằng thước kẻ.
Hỗn số 2 và ![]() được viết thành số thập phân là:
được viết thành số thập phân là:
2,625
2,16
0,2625
0,216
Chứng minh rằng A = 8101 – 5 không phải là số chính phương.
Tìm GTLN của a2 + b2 + c2 biết a, b, c thỏa mãn 1 ≤ a, b, c ≤ 2 và a + b + c = 6.
Cho 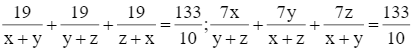 .
.
Tính x + y + z?
Cho 2 tập hợp A = [m + 1; 2m − 1], B = (0;6). Có bao nhiêu giá trị nguyên của m để A là tập con của B?
Cho 30 điểm trong đó có đúng 5 điểm thẳng hàng. Cứ qua 2 điểm ta vẽ được 1 đường thẳng. Hỏi có tất cả bao nhiêu đường thẳng?
Cho A(-2;-3), B(4;-1), C(2;1), D(1;0).
a) Chứng minh ABCD là hình thang.
b) Tìm tọa độ giao điểm giữa AB và Ox.
c) Tìm tọa độ giao điểm giữa AC và BD.
Cho 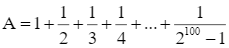 . Chứng minh 50 < A.
. Chứng minh 50 < A.
Cho 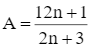 .
.
a) Tìm giá trị của n để A là số nguyên.
b) Tìm giá trị của n để A là phân số.
Chứng minh rằng A = 21 + 22 + … + 2100 chia hết cho 3.
Cho 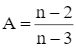 . Tìm điều kiện của n để A là một phân số.
. Tìm điều kiện của n để A là một phân số.
Cho tam giác ABC có ![]() và có phân giác AD. Tính
và có phân giác AD. Tính ![]() ?
?
Cho B = 1 + 3 + 32 + 33 + … + 311. Chứng minh rằng B chia hết cho 13.
Cho biết 15 công nhân hoàn thành công việc 12 ngày. Hỏi để hoàn thành công việc trong 8 ngày thì cần bao nhiêu công nhân? (biết năng suất làm việc của mỗi công nhân là như nhau).
Cho cấp số cộng (un) thỏa mãn: 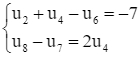 .
.
Tính S7 = u1 + u2 + … + u7
Cho các dãy số : 0,1,4,9,16,....2401. Tập hợp A gồm các số hạng của dãy số trên được biểu diễn bằng cách chỉ ra tính chất đặc trưng cho các phần tử của tập hợp là?
Tính tổng sau. 10,11 + 11,12 + 12,13 + 13,14 + ... + 98,99.
Cho điểm K nằm trong tam giác ABC. Gọi M là giao điểm của tia AK với cạnh BC.
a) Chứng minh rằng KA+KB < MA+ MB < CA + CB.
b) So sánh KB+ KC với AB +AC.
c) Chứng minh rằng : KA+ KB + KC < PABC.
Cho đường thăng a và một điểm O cách a một khoảng 8cm. Vẽ đường tròn tâm O bán kính 10cm.
a) Giải thích vì sao a và (O) cắt nhau.
b) Gọi M và N là các giao điểm của đường thẳng a và đường tròn (O;10cm). Tính độ dài của dây MN.
Cho đường thẳng Δ: x - 3y + 1 = 0. Tìm 1 vectơ chỉ phương và 1 vectơ pháp tuyến của đường thẳng Δ.
Cho đường tròn (C) tâm O, bán kính r = 20 cm. Vẽ đường tròn(C') đi qua tâm O và tiếp xúc với (C), vẽ đường tròn (C'') đi qua tâm của (C) và tiếp xúc với (C'). Tiếp tục quá trình này đến hạn. Tình tổng diện tích các đường tròn tạo thành.
Cho đường tròn (O; R) đường kính AB. Qua trung điểm I của bán kính OB. Kẻ dây CD vuông góc với AB. Kẻ dây CE song song dây AB.
a, Chứng minh AE = BC = BD.
b, Chứng minh E, O, D thẳng hàng.
c, Chứng minh tứ giác ADBE là hình chữ nhật.
Cho 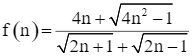 với n nguyên dương.
với n nguyên dương.
Tính f(1) + f(2) + f(3) + … f(40).
Cho góc α (0° < α < 180°), giá trị của biểu thức ![]() bằng bao nhiêu?
bằng bao nhiêu?
Cho hàm số 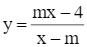 (m là tham số). Có bao nhiêu giá trị nguyên của tham số m để hàm số đồng biến trên khoảng (0; +∞)?
(m là tham số). Có bao nhiêu giá trị nguyên của tham số m để hàm số đồng biến trên khoảng (0; +∞)?
Cho hình bình hành ABCD có AB = 2a, AD = 3a, ![]() . Điểm K thuộc AD thỏa mãn
. Điểm K thuộc AD thỏa mãn ![]() . Tính tích vô hướng
. Tính tích vô hướng ![]() .
.
Cho hình bình hành ABCD có AB = 3a; ![]() ; góc B tù; diện tích hình bình hành = 6a2. Tính độ dài đường chéo BD.
; góc B tù; diện tích hình bình hành = 6a2. Tính độ dài đường chéo BD.
Cho hình bình hành ABCD có AB = 2; AD = 1, ![]() . Tính độ dài đường chéo AC và BD.
. Tính độ dài đường chéo AC và BD.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm của SB, SD, OC.
a) Tìm giao tuyến của mặt phẳng (MNP) với mp (SAC).
b) Tìm giao điểm của SA với mp (MNP).
c) Tìm thiết diện của S.ABCD với (AMN).
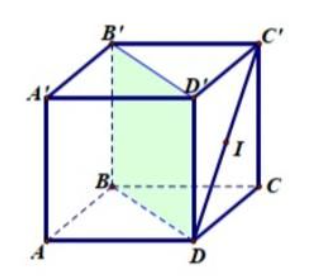
Cho hình lập phương ABCD.A’B’C’D’ cạnh ![]() , I là trung điểm CD’. Tính khoảng cách từ I đến mặt phẳng (BDD’B’).
, I là trung điểm CD’. Tính khoảng cách từ I đến mặt phẳng (BDD’B’).
Hình thang ABCD có đáy AB = 9cm và đáy CD = 12cm. Nếu kéo chiều dài đáy bé thêm đoạn BE 4cm và kéo chiều dài đáy lớn thêm đoạn CQ = 5cm thì diện tích ABCD sẽ tăng thêm 135cm2. Tính diện tích hình thang ABCD.
Cho hình thang ABCD có AB // CD . Lấy I là trung điểm của DC. Từ I kẻ IM // AC (M = AD) và IN // BD (N = BC)
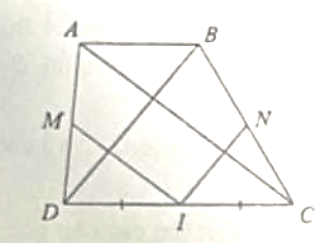
a) Chứng minh 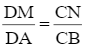
b) Chứng minh MI.BD = IN.AC
Cho hình vẽ biết Ax // My, ![]() . Az là tia phân giác của
. Az là tia phân giác của ![]() . Tính số đo của
. Tính số đo của ![]() .
.

Cho hình vẽ bên, biết ABCD là hình bình hành, DI // EF, BK // EF. Chứng minh rằng 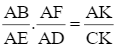 .
.
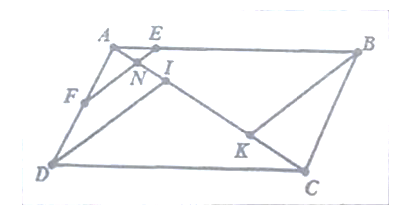
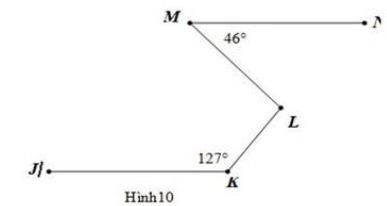
Cho hình 10, biết ![]() , MN // KJ. Hãy tính số đo
, MN // KJ. Hãy tính số đo ![]() .
.
Cho hình vuông ABCD có diện tích là 20cm2 (hình bên). Tính diện tích phần tô màu.

Cho hình vuông ABCD cạnh a. Tính theo a độ dài ![]() .
.
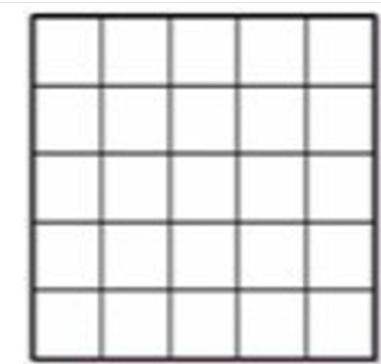
Cho hình vuông lớn (5x5) như hình có chứa số lượng lớn hình chữ nhật bao gồm cả hình vuông. Mỗi hình chữ nhật được tạo thành từ 1 đến 25 ô vuông nhỏ. Tìm tất cả các hình chữ nhật chứa trong hình vuông lớn (bao gồm cả hình vuông).
Cho ![]() . Hỏi mệnh đề nào sau đây đúng?
. Hỏi mệnh đề nào sau đây đúng?
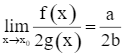
![]()
![]()
![]()
Cho A = n3 + 2025n2 + 2024n. Chứng minh A chia hết cho 3 với mọi n nguyên dương.
Cho phân thức 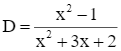 .Tìm ĐKXĐ của phân thức.
.Tìm ĐKXĐ của phân thức.
Cho phân thức 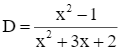 .Rút gọn phân thức và tính giá trị D khi x= 2002.
.Rút gọn phân thức và tính giá trị D khi x= 2002.
Cho phương trình x2 - 2(m - 1)x + m + 1 = 0.
Với giá trị nào của m thì phương trình có 2 nghiệm phân biệt.
Cho phương trình x2 - 2(m - 1)x + m + 1 = 0.Tìm m để phương trình có 2 nghiệm x1, x2 thỏa mãn x1 = 3x2.
Giải phương trình: 2x2 + 3x + 1 = 0.
Cho phương trình: x² - (m - 4)x – m - 2 = 0 (x là ẩn, m là tham số) (1). Giải phương trình (1) với m = -2.
Cho phương trình x2 + 5x – 3m = 0 (m là tham số).Tìm tham số m để phương trình có 2 nghiệm là x1 và x2.
Cho phương trình x2 + 5x – 3m = 0 (m là tham số).Với điều kiện m tìm được ở câu a) hãy lập một phương trình bậc hai có hai nghiệm là ![]() và
và ![]() .
.
Cho 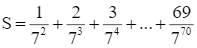 . Chứng minh
. Chứng minh 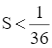 .
.
Cho tam giác ABC.kẻ tia phân giác AI. Từ B và C hạ BD và CE lần lượt vuông góc với tia AI.
Chứng minh 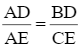 .
.
Cho tam giác ABC.kẻ tia phân giác AI. Từ B và C hạ BD và CE lần lượt vuông góc với tia AI.Chứng minh ID.CE = BD.IE.
Cho tam giác ABC. Trên BC lấy D. Qua D kẻ DE // AC, DF // AB (E thuộc AB, F thuộc AC).
Chứng minh AEDF là hình bình hành.
Cho tam giác ABC. Trên BC lấy D. Qua D kẻ DE // AC, DF // AB (E thuộc AB, F thuộc AC).Chứng minh BE.DC = AE.BD.
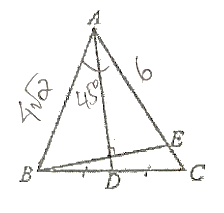
Cho tam giác ABC có AB nhỏ hơn AC, AD là tia phân giác của góc A (D thuộc BC). Trên AC lấy điểm E sao cho AE = AB.
So sánh: DC và DB.
Cho tam giác ABC có AB nhỏ hơn AC, AD là tia phân giác của góc A (D thuộc BC). Trên AC lấy điểm E sao cho AE = AB.So sánh: ![]() và
và![]() .
.
Cho tam giác ABC bằng tam giác HIK biết AB = 7cm, BC= 8cm, HK 7 cm.
Cạnh AC bằng bao nhiêu cm?
Cho tam giác ABC bằng tam giác HIK biết AB = 7cm, BC= 8cm, HK 7 cm.Tính chu vi của mỗi tam giác trên.
Cho tam giác ABC có ba góc nhọn, AB < AC. Qua trung điểm D của cạnh BC kẻ đường thẳng vuông góc với tia phân giác của góc BAC cắt các đường thẳng AB và AC lần lượt tại H và K. Chứng minh rằng: tam giác AHK cân.
Cho tam giác ABC có ba góc nhọn, AB < AC. Qua trung điểm D của cạnh BC kẻ đường thẳng vuông góc với tia phân giác của góc BAC cắt các đường thẳng AB và AC lần lượt tại H và K. Qua B kẻ đường thẳng song song với AC cắt HK tại I . Chứng minh rằng: tam giác BHI cân.
Cho tam giác ABC có ba góc nhọn, AB < AC. Qua trung điểm D của cạnh BC kẻ đường thẳng vuông góc với tia phân giác của góc BAC cắt các đường thẳng AB và AC lần lượt tại H và K. Chứng minh: BH = CK.
Cho tam giác ABC có ba góc nhọn, AB < AC. Qua trung điểm D của cạnh BC kẻ đường thẳng vuông góc với tia phân giác của góc BAC cắt các đường thẳng AB và AC lần lượt tại H và K. Tính AH, BH biết AB = 9cm, AC = 12cm.
Cho tam giác ABC có A (-1;2), B (0;3), C (5;-2). Tìm toạ độ chân đường cao hạ từ đỉnh A của tam giác ABC.
Cho tam giác ABC có ![]() . Gọi D là trung điểm của BC, E thỏa mãn AE = kAC (k ∈ ℝ). Khi đó:
. Gọi D là trung điểm của BC, E thỏa mãn AE = kAC (k ∈ ℝ). Khi đó:
a) AD vuông góc BE khi 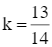
b) ![]() = 20
= 20
c) 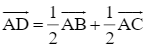
d) ![]()
Cho tam giác ABC có chu vi bằng 36cm. Trên AB lấy điểm E sao cho AB = 3BE. Từ E kẻ EF//AC (F BC). Chu vi tam giác BEF bằng bao nhiêu cm?
Cho tam giác ABC có diện tích 64cm2. M là trung điểm của BC, N là trung điểm của AM. Tính diện tích tam giác BNC.
Chọn đúng hoặc sai cho mệnh đề sau: “Phương trình đường cao kẻ từ A là 5x - 7y – 6 = 0”. Với giả thiết đề bài: Cho tam giác ABC có phương trình đường thẳng BC là 7x + 5y – 8 = 0, phương trình đường cao kẻ từ B, C lần lượt là 9x - 3y – 4 = 0, x + y – 2 = 0.
Cho tam giác ABC (AB < AC) , đường phân giác AD. Qua trung điểm M của BC, kẻ đường thẳng song song với AD, cắt AC, AB theo thứ tự ở E và K. Gọi O là giao điểm của AM và DK. Chứng minh AO. OK = DO . OM.
Cho tam giác ABC (AB < AC) , đường phân giác AD. Qua trung điểm M của BC, kẻ đường thẳng song song với AD, cắt AC, AB theo thứ tự ở E và K. Gọi O là giao điểm của AM và DK. Cho AB = 5 cm, AC = 10 cm, BC = 12 cm. Tính BD.
Cho tam giác ABC (AB < AC) , đường phân giác AD. Qua trung điểm M của BC, kẻ đường thẳng song song với AD, cắt AC, AB theo thứ tự ở E và K. Gọi O là giao điểm của AM và DK. Chứng minh AE = AK và 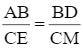 .
.
Cho tam giác ABC (AB < AC) , đường phân giác AD. Qua trung điểm M của BC, kẻ đường thẳng song song với AD, cắt AC, AB theo thứ tự ở E và K. Gọi O là giao điểm của AM và DK. Chứng minh BK = CE.
Cho tam giác ABC, gọi I là điểm trên BC kéo dài sao cho IB = 3IC. Gọi J và K lần lượt là hai điểm trên cạnh AC, AB sao cho JA = 2JC, KB = 3KA. Biểu diễn BC theo AI, JK.
Cho tam giác ABC, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA.Chứng minh tam giác AMC = tam giác EMB.
Cho tam giác ABC, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA.
AC // BE.
Cho tam giác ABC, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA.Gọi I là 1 điểm trên AC, K là 1 điểm trên EB sao cho AI = EK. Chứng minh 3 điểm I, M, K thẳng hàng.
Cho ABC nhọn. Trên tia đối của tia AB lấy điểm M sao cho AM = AB. Trên tia đối của tia AC lấy điêm N sao cho AN = AC.
Chứng minh AMN = ABC
Cho ABC nhọn. Trên tia đối của tia AB lấy điểm M sao cho AM = AB. Trên tia đối của tia AC lấy điêm N sao cho AN = AC.Chứng minh MN // BC
Cho ABC nhọn. Trên tia đối của tia AB lấy điểm M sao cho AM = AB. Trên tia đối của tia AC lấy điêm N sao cho AN = AC.Lấy điểm F thuộc cạnh BC. Trên tia đối của tia AF lấy điểm E sao cho AE = AF. Chứng minh ba điểm M, E, N là ba điểm thẳng hàng.
Cho tam giác ABC nội tiếp (O). Tia phân giác góc A cắt đường tròn tại M, tia phân giác góc ngoài tại đỉnh A cắt đường tròn tại N.
Chứng minh tam giác MBC cân.
Cho tam giác ABC nội tiếp (O). Tia phân giác góc A cắt đường tròn tại M, tia phân giác góc ngoài tại đỉnh A cắt đường tròn tại N.Chứng minh: O, M, N thẳng hàng.
Cho tam giác ABC. Trên cạnh AB lấy điểm M sao cho 2BA = 5BM. Gọi G là trọng tâm tam giác ABC. Gọi N trên cạnh AC sao cho AN = xAC. tìm x biết M, N, G thẳng hàng.
Cho tam giác ECD. trên các cạnh ED, EC lần lượt lấy các điểm A và B sao cho góc ![]() . Gọi O là giao điểm của AC và BD. Chứng minh tam giác EAB đồng dạng tam giác ECD.
. Gọi O là giao điểm của AC và BD. Chứng minh tam giác EAB đồng dạng tam giác ECD.
Cho tam giác ECD. trên các cạnh ED, EC lần lượt lấy các điểm A và B sao cho góc ![]() . Gọi O là giao điểm của AC và BD. Chứng minh tam giác EAC đồng dạng tam giác tam giác EBD.
. Gọi O là giao điểm của AC và BD. Chứng minh tam giác EAC đồng dạng tam giác tam giác EBD.
Cho tam giác ECD. trên các cạnh ED, EC lần lượt lấy các điểm A và B sao cho góc ![]() . Gọi O là giao điểm của AC và BD. Chứng minh OA.OC = OB.OD.
. Gọi O là giao điểm của AC và BD. Chứng minh OA.OC = OB.OD.
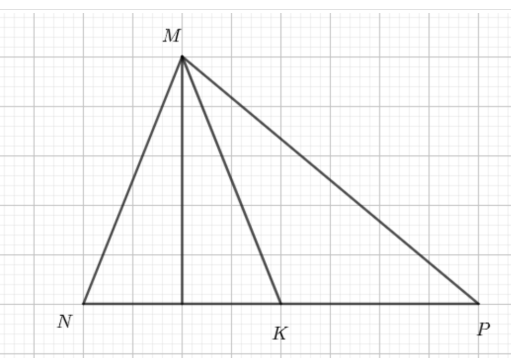
Cho hình tam giác MNP, trên NP lấy điểm K sao cho NK = ![]() NP, nối MK [như hình vẽ]. Tính diện tích hình tam giác MNP, biết diện tích hình tam giác MNK bằng 54cm2
NP, nối MK [như hình vẽ]. Tính diện tích hình tam giác MNP, biết diện tích hình tam giác MNK bằng 54cm2
Cho 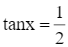 . Tính giá trị biểu thức P = 25(sin4x + cos4x).
. Tính giá trị biểu thức P = 25(sin4x + cos4x).
Cho 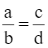 . Chứng minh
. Chứng minh 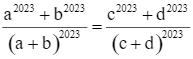 .
.
Cho tổng S = 31 + 32 + … + 320. Chứng minh S chia hết cho 12.








