10000 câu trắc nghiệm tổng hợp môn Toán 2025 mới nhất (có đáp án) - Phần 31
100 câu hỏi
Tìm số dư trong phép chia 340 chia cho 83.
Tìm số dư của phép chia 3517 cho 25.
Tìm số nguyên tố ab (a > b > 0) với ab – ba là số chính phương
Tìm số nguyên tố x, y biết 19x4 + 57 = y2
Tìm số nguyên x, y biết: x2y – x + xy = 6
Tìm n để n2 – 2n + 2020 là một số chính phương
Tìm số tự nhiên n biết: 2n + 3n = 5n
Tìm x, biết: [(6x – 39) : 7].4 = 12
Tìm x, y, z biết \(\frac{x}{3} = \frac{y}{4} = \frac{z}{5}\) và xyz = 480
Tính: \(\frac{1}{{1.1985}} + \frac{1}{{2.1986}} + \frac{1}{{3.1987}} + ... + \frac{1}{{16.2000}}\)
Tính \(\frac{7}{9} \times \frac{5}{6}\)
Tính bằng cách thuận tiện nhất: 1 + 2 + 3 + 4 + ... + 9
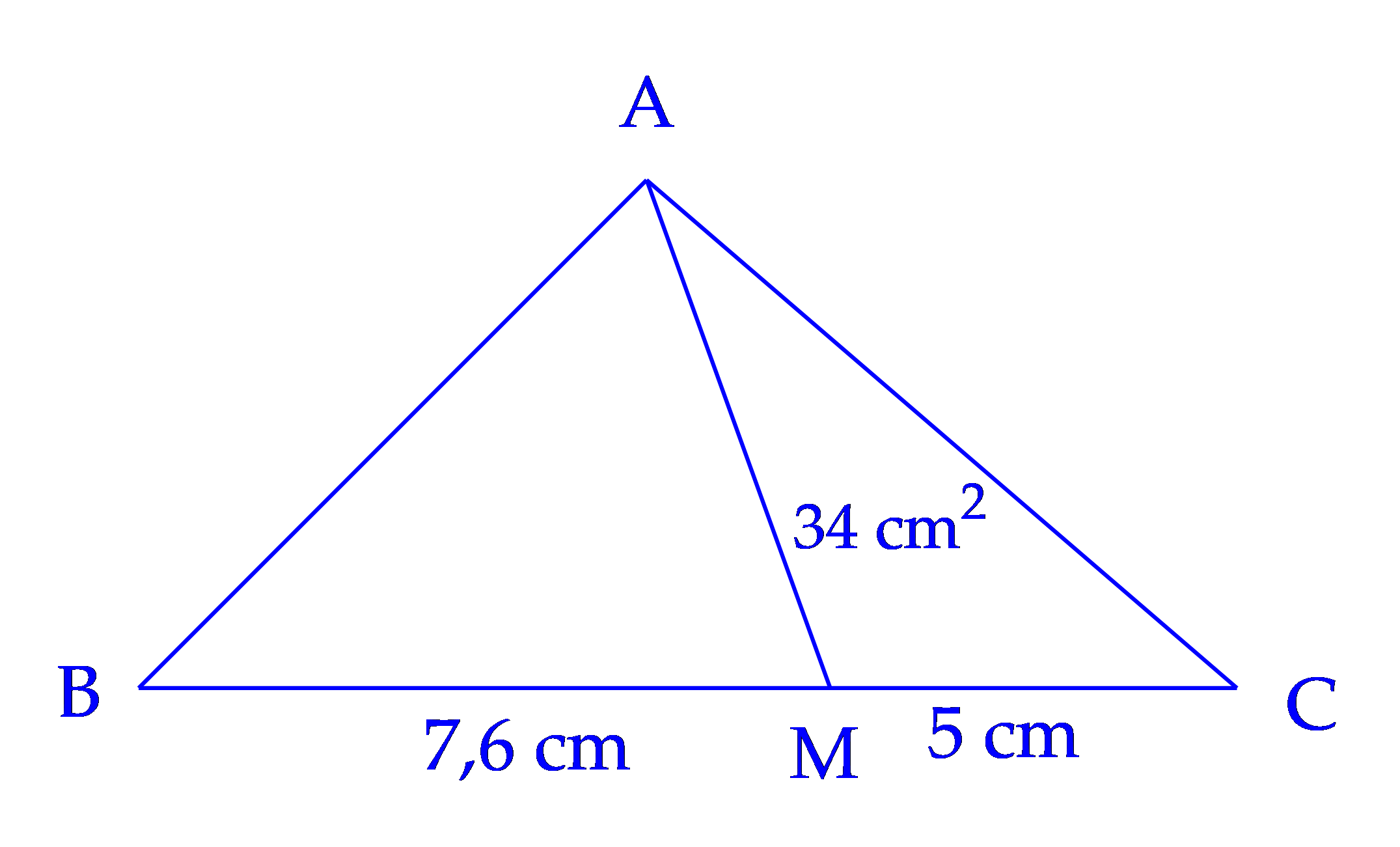
Tính diện tích hình tam giác ABM (như hình vẽ), biết diện tích hình tam giác AMC là 34 cm2.
Tính giá trị biểu thức B = x6 – 50x5 + 50x4 – 50x3 + 50x2 – 50x + 50 tại x = 49.
Tìm giá trị nhỏ nhất của A = 2(x – 1)2 - 2024
Tính: 159(18 – 59) – 59(19 – 159)
Tính nhanh: \(\frac{1}{{15}} + \frac{1}{{21}} + \frac{1}{{28}} + \frac{1}{{36}} + \frac{1}{{45}} + \frac{1}{{55}}\)
Tỉ số phần trăm của 9 và 15 là gì?
Tìm tổng của số chẵn lớn nhất có một chữ số với số liền trước của số nhỏ nhất có hai chữ số.
Trên 1 khu đất hình chữ nhật chiều rộng 12 m và bằng chiều dài, người ta đắp một nền nhà hình vuông chu vi 24 m và xây một bồn hoa hình tròn bán kính 2 m, chung quanh vườn hoa, người ta làm một lối đi chiếm diện tích 15,70 m2. Tính diện tích đất còn lại?
Cho đường thẳng d: x – 2y + 4 = 0 và điểm A(4; 1). Tìm tọa độ hình chiếu vuông góc của A lên d.
Trong mặt phẳng tọa độ, cho các điểm A(0; 2); B(1; 1); C(-1; -2). Các điểm A', B', C' lần lượt chia các đoạn BC, CA, AB theo các tỉ số -1; \(\frac{1}{2}\); -2. Tìm tọa điểm các điểm A', B', C'?
Trong mặt phẳng tọa độ Oxy, cho tam giác DEF có D(1; -1); E(2; 1), F(3; 5). Khi đó:
| Mệnh đề | Đúng | Sai |
(a) | Đường thẳng vuông góc với đường thẳng EF nhận \(\overrightarrow {EF} \) là một vectơ chỉ phương |
|
|
(b) | Phương trình đường cao kẻ từ D là: x + y = 0 |
|
|
(c) | Gọi I là trung điểm của DF. Tọa độ của điểm I là (2; 2) |
|
|
(d) | Đường trung tuyến kẻ từ E có phương trình: x – 2 = 0 |
|
|
Trong một vòng thi Olympic Toán gồm có 15 câu hỏi với thể lệ như sau: Mỗi câu trả lời đúng thí sinh được 5 điểm, mỗi câu trả lời sai thí sinh bị trừ 2 điểm. Bạn Bảo sau khi trả lời tất cả các câu hỏi của vòng thi này và đạt được 40 điểm. Hỏi bạn Bảo đã trả lời đúng bao nhiêu câu?
Từ 1 đến 99 có bao nhiêu số lẻ?
1 can đựng được 9 lít dầu nặng 9,3 kg can rỗng nặng 1,65 kg. Hỏi mỗi lít dầu cân nặng bao nhiêu kg.
Tìm ước chung lớn nhất rồi tìm tập hợp ước chung của 80 và 150.
Vào tháng 5, gián niêm yết của một chiếc TV 42 inch tại một siêu thị điện máy là 8 000 000 đồng. Đến tháng 8, siêu thị giảm giá 5% cho mỗi chiếc TV. Sang tháng 9, siêu thị lại giảm giá thêm một lần nữa, lúc này giá của một chiếc TV 42 inch chỉ còn 6 840 000 đồng. Hỏi tháng 9, siêu thị đã giảm giá bao nhiêu phần trăm cho một chiếc TV so với tháng 8.
Viết tất cả các phân số bằng \(\frac{{13}}{{17}}\) mà tử và mẫu là 2 số tự nhiên có 2 chữ số
Sắp xếp từ nhỏ đến lớn: \(\frac{{26}}{{27}};\frac{{25}}{{26}};\frac{{51}}{{52}};\frac{{52}}{{53}}\)
Viết phường trình tiếp tuyến d của đường tròn (C): (x + 3)2 + (y – 3)2 = 25, biết d hợp với trục Ox góc 45°
Tìm x biết \(x - \left( { - \frac{{18}}{{54}}} \right) = \frac{7}{9}\)
Tìm x sao cho x \( \vdots \) 12 và 13 < x < 75
Tìm x biết: \(\frac{{x + 1}}{{11}} - \frac{{2x - 5}}{{15}} = \frac{{3x - 47}}{{17}} - \frac{{4x - 59}}{{19}}\)
Cho x : y : z = 2: 3 : 5 và xyz = 810. Tính x + y + z
Tìm x, y biết: \(\frac{x}{3} = \frac{y}{7}\) và x2 + y2 = 58
Tìm x nguyên biết: \(\frac{x}{3} - \frac{1}{{y + 1}} = \frac{1}{6}\)
Tìm x, y, z biết \(\frac{x}{5} = \frac{y}{7} = \frac{z}{2}\) và y – x = 48
Tìm x, y biết: x: y = 3 : 5 và 2x – y = 14
Tìm giá trị của m để bất phương trình x2 + 2mx – 2m + 3 ³ 0 có tập nghiệm \(\mathbb{R}\).
Chứng minh rằng: Nếu \(\frac{{{x^2} - yz}}{a} = \frac{{{y^2} - zx}}{b} = \frac{{{z^2} - xy}}{c}\) thì \(\frac{{{a^2} - bc}}{x} = \frac{{{b^2} - ca}}{y} = \frac{{{c^2} - ab}}{z}\)
Phân tích thành nhân tử: x5 + x4 + x3 + x2 + x + 1
Chứng minh rằng phương trình x7 + 3x5 – 1 = 0 có ít nhất 1 nghiệm.
Khai triển \(x_1^3 - x_2^3\)
Tìm x biết: \(\frac{{x - 1}}{{2011}} + \frac{{x - 2}}{{2010}} - \frac{{x - 3}}{{2009}} = \frac{{x - 4}}{{2008}}\)
Chứng minh đẳng thức sau: \(\frac{{{x^2} + 3x - 4}}{{x - 1}} = x + 4\) với x ¹ 1
Tìm x, y nguyên để x2 + xy – 3x – 3y + 7 = 0
Tìm các cặp số nguyên x, y biết xy + 7x – 3y – 26 = 0
Tìm cặp số nguyên x; y biết: xy – x – y = 2
Giải hệ phương tình: \(\left\{ \begin{array}{l}{y^2} = {x^3} - 3{x^2} + 2x\\{x^2} = {y^3} - 3{y^2} + 2y\end{array} \right.\)
Rút gọn biểu thức sau \[A = \frac{{\sin 3x - \sin x}}{{2{{\cos }^2}x - 1}}\]
Chứng minh 1 + 2 + 22 + 23 + … + 22015 không phải là số chính phương
Chứng minh 1 + 2 + 22 + 23 + … + 22015 không phải là số chính phương
Một bánh xe có đường kính là 65 cm. Bánh xe đó lăn trên một đoạn đường dài 1,0205 km. Hỏi bánh xe đó lăn được bao nhiêu vòng?
Cho hai số nguyên x, y với x > 1 thỏa mãn 2x2 – 1 = y15 . Chứng minh x chia hết cho 15
Bánh xe đạp có đường kính 55 cm (kể cả lốp). Nếu chạy với vận tốc 40 km/h thì trong 25 s bánh xe quay được số vòng bằng bao nhiêu?
Biết tứ giác MNPQ nội tiếp đường tròn (O) có \[\widehat {MNP} = 2\widehat {MQP}\]. Tính số đo \[\widehat {NOP}\]= ?
Cân nặng (đơn vị kg) của 12 em học sinh tổ 3 lớp 10A được cho bởi mẫu liệu sau: 36, 80, 50, 70, 48, 47, 47, 43, 42, 40, 41, 47. Mẫu số liệu trên có bao nhiêu giá trị bất thường?
Tính diện tích hình tròn ngoại tiếp tam giác đều cạnh a là:
Cho a + b = 2 và a2 + b2 = 20 . Tính M = a3 + b3
Cho hàm số f(x) = 2x3 + ax2 + bx + c có f(0) = 2f'(0) và f(x) ≥ 2f'(x) với mọi x ≥ ‒1. Có bao nhiêu giá tị nguyên của a để hàm số f(x) đồng biến trên ℝ?
Vô số.
11.
1.
10.
Cho hệ bất phương trình \[\left\{ \begin{array}{l}x + 2y - 5 \le 0\\0 \le x \le 3\\y \ge 0\end{array} \right.\]. Xét tính đúng sai của các khẳng định sau:
a) Bộ số (0; 0) là một nghiệm của hệ đã cho.
b) Bộ (2; 1) là một nghiệm của hệ đã cho.
c) Biểu diễn miền nghiệm của hệ trên là một đa giác có diện tích bằng 6.
d) Xét tất cả các bộ số (x; y) thỏa mãn hệ trên thì giá trị lớn nhất của biểu thức 2x + y bằng 7.
Cho hình chóp đều S.ABCD tâm O, có \[SD = a\sqrt 2 \] và \[BC = a\sqrt 3 \]. Tính \[\left| {\overrightarrow {SA} + \overrightarrow {SC} } \right|.\]
Cho hình chóp tứ giác đều S.ABCD có độ dài tất cả các cạnh bằng a. Tính tích vô hướng \[\overrightarrow {{\rm{AS}}} \cdot \overrightarrow {BC} = x\], \[\overrightarrow {{\rm{AS}}} \cdot \overrightarrow {AC} = y\]. Khi đó \[\frac{x}{y}\] bằng bao nhiêu?
Cho hình lăng trụ tam giác đều. Trong các mệnh đề sau mệnh đề nào là sai?
Hai đáy là các tam giác đều bằng nhau.
Các mặt bên là hình vuông.
Các cạnh bên vuông góc với mặt đáy.
Các cạnh bên bằng nhau.
Cho hình thang ABCD (AB // CD), gọi O là giao điểm của hai đường chéo AC và BD. Qua O kẻ đường thẳng song song với AB cắt AD và BC lần lượt ở M và N. Chứng minh rằng OM = ON.
Cho một tấm nhôm có dạng hình vuông cạnh 10 dm. Nếu tăng cạnh của hình vuông lên 10 dm thì diện tích hình vuông tăng lên bao nhiêu dm2?
Cho parabol (P): y = x2 ‒ 2x + 5 và đường thẳng d: y = 2mx + 2 ‒ 3m. Tìm tất cả các giá trị m để (P) cắt d tại hai điểm phân biệt nằm phía bên phải trục tung?
\[1 < m < \frac{7}{3}.\]
m > 1.
\[m > \frac{7}{3}.\]
m < 1.
Cho tam giác ABC cân tại A có \[\widehat A = 120^\circ \] nội tiếp đường tròn (O; 3 cm). Khi đó diện tích tam giác ABC là
\[\frac{{9\sqrt 3 }}{4}\] cm2.
\[\frac{{3\sqrt 3 }}{2}\] cm2.
\[3\sqrt 3 \] cm2.
\[\frac{{3\sqrt 3 }}{4}\] cm2.
Cho tam giác ABC có ba góc nhọn, đường cao AH. Ở miền ngoài của tam giác ABC vẽ các tam giác vuông cân ABE và ACF và tam giác ACF đều nhận A làm đỉnh góc vuông. Kẻ EM, FN cùng vuông góc với AH (M, N thuộc AH).
a) Chứng mình rằng: EM + HC = NH.
b) Chứng minh rằng: EN // FM.
Cho tam giác ABC đều cạnh a, M là trung điểm của BC. Tính \[\overrightarrow {CA} - \overrightarrow {MC} .\]
Cho tam giác ABC đều có cạnh bằng 8. Biết tập hợp tất cả các điểm N thỏa mãn \[\left| {3\overrightarrow {NA} - 2\overrightarrow {NB} + \overrightarrow {NC} } \right| = \left| {\overrightarrow {NB} - \overrightarrow {NA} } \right|\] là một đường tròn có bán kính R. Tính R.
Có 13 đoạn que gồm 3 đoạn que mỗi đoạn dài 1cm, 3 đoạn que mỗi đoạn dài 2 cm, 6 đoạn que mỗi đoạn dài 4 cm, 1 đoạn que dài 5 cm. Hỏi phải bỏ đi đoạn que nào để 12 đoạn que còn lại xếp nối thành hình vuông? Hãy nêu một cách xếp nối đó. Tính độ dài cạnh hình vuông đã được xếp nối.
Có bao nhiêu số palindrom gồm 5 chữ số (Số palindrom là số mà nếu ta viết các chữ số theo thứ tự ngược lại thì giá trị của nó không thay đổi):
900.
10 000.
810.
729.
Cô phương thống kê lại số giờ chơi thể thao trong 1 tuần của học sinh lớp 10C ở bảng sau:
Số giờ | [0; 3) | [3; 6) | [6; 9) | [9; 12) |
Số học sinh | 3 | 10 | 14 | 23 |
Chọn đúng hoặc sai cho các câu sau:
a) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là 12 giờ.
b) Tứ phân vị thứ nhất của mẫu số liệu gốc thuộc [3; 6).
c) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là \[\frac{{681}}{{460}}.\]
d) Phương sai của mẫu số liệu ghép nhóm trên là 7,9236.
Công ty TNHH A dự định sản xuất ít nhất 80 kg đường vàng và 20 kg đường trắng từ hai nguyên liệu là mía và củ cải. Từ một tạ mía giá 600 nghìn đồng có thể sản xuất 40 kg đường vàng và 50 kg đường trắng. Từ một tạ củ cải giá 300 nghìn đồng có thể sản xuất 8 kg đường vàng và 4 kg đường trắng. Nhưng nhà cung cấp nguyên liệu cho công ty chỉ còn 8 tạ mía và 12 tạ củ cải. Hỏi chi phí mua nguyên liệu của công ty ít nhất là bao nhiêu nghìn đồng?
Có 6 bạn nam trong đó có Hoàng và 3 bạn nữ xếp ngẫu nhiên thành một hàng ngang. Xác xuất để không có hai bạn nữ nào đứng cạnh nhau và Hoàng đứng ở ngoài cùng bằng
\[\frac{{10}}{{21}}.\]
\[\frac{5}{{126}}.\]
\[\frac{5}{{21}}.\]
\[\frac{5}{{63}}.\]
Diện tích một trang của một cuốn sách là 600 cm2. Do yêu cầu kĩ thuật, cần để lề trên và lề dưới là 3 cm, lề tráo và lề phải là 2 cm. Tính chiều dài của trang giấy để diện tích phần chữ in vào cuốn sách được nhiều nhất?
Diện tích S của hình phẳng giới hạn bởi đồ thị hai hàm số y = x2 ‒ 2x và y = x là
\[S = \frac{9}{4}.\]
\[S = \frac{9}{2}.\]
\[S = \frac{{13}}{2}.\]
\[S = \frac{{13}}{4}.\]
Diện tích của năm tỉnh Kon Tum, Gia Lai, Đăk Lăk, Đăk Nông và Lâm Đồng được thống kê ở bảng sau:
Tỉnh | Kon Tum | Gia Lai | Đăk Lăk | Đăk Nông | Lâm Đồng |
Diện tích (km2) | 9 674 | 15 510 | 13 030 | 6 509 | 9 783 |
Tổng diện tích năm tỉnh Kon Tum, Gia Lai, Đăk Lăk, Đăk Nông và Lâm Đồng bằng bao nhiêu phần trăm diện tích miền Nam Việt Nam (làm tròn kết quả đến hàng đơn vị), biết diện tích miền Nam Việt Nam là 77 700 km2)?
70%.
71%.
69%.
61%.
Cho các hàm số y = logax và y = logbx có đồ thị như hình vẽ
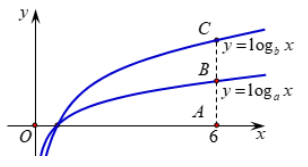
Đường thẳng x = 6 cắt trục hoành, đồ thị hàm số y = logax và y = logbx lần lượt tại A, B và C. Nếu \[\frac{{AC}}{{AB}} = {\log _2}3\] thì khẳng định nào sau đây là đúng?
b2 = a3.
b3 = a2.
log2b = log3a.
log3b = log2a.
Giả sử chi phí mua và bảo trì một thiết bị trong x năm có thể được mô hình hóa theo công thức \[C = 5\,\,000\left( {25 + 3\int\limits_0^x {{t^{\frac{1}{4}}}} dt} \right).\] Xét tính đúng sai của các khẳng định sau:
a) Chi phí mua 1 sản phẩm là 100 000 đồng.
b) Chi phí bảo trì năm đầu tiên của 1 sản phẩm là 12 000 đồng.
c) Sau 6,5 năm thì số tiền mua một sản phẩm bằng số tiền bảo trì sản phẩm đó.
d) Nếu một nhà đầu tư có 10 triệu, thì họ có thể mua và bảo trì tối đa 30 sản phẩm trong 10 năm.
Giá trị lớn nhất của hàm số f(x) = ‒x4 + 6x2 ‒ 4 bằng
A. \[ - \sqrt 3 .\]
B. ‒4.
C. 5.
D. \[\sqrt 3 .\]
Cho bất phương trình log2(5x ‒ 1) ≤ m.
Gọi S là tập hợp tất cả các giá trị nguyên của m sao cho bất phương trình có đúng 3 nghiệm nguyên. Số phần tử của S là
A. 0.
B. 1.
C. 2.
D. 3.
Hai bạn An và Bình đến một nhà sách để mua bột và vợ bạn An mua 5 chiếc bút và 10 quyển vở với tổng số tiền là 230 000 đồng. Bạn bình mua 10 chiếc bút và 8 quyển vở với tổng số tiền 220 000 đồng. Tính giá bán của mỗi chiếc bút và của mỗi quyển vở biết rằng hai bạn An và Bình mua cùng loại bút và vở.
Hàng ngày, mực nước của con kênh lên xuống theo thủy triều. Độ sâu h (mét) của mực nước trong kênh tính theo thời gian t (giờ) trong một ngày (0 ≤ t < 24) cho bởi công thức \[h = \cos \left( {\frac{{\pi t}}{6} + 2\pi } \right) + 5\]. Hỏi trong ngày mực nước xuống thấp nhất trễ nhất là mấy giờ?
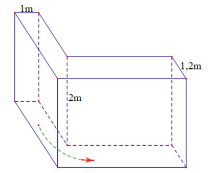
Hành lang trong một tòa nhà có dạng chữ L (hình vẽ) có chiều cao 2 m, một phía rộng 1m, một phía rộng 1, 2 m. Một người thợ cần mang một số ống thép cứng các loại có độ dài 2 m, 2, 5 m, 3 m, 3,5 m, 4 m, từ bên này qua bên kia. Hỏi có thể mang được mấy loại qua lối đi đó?
4 loại.
3 loại.
5 loại.
2 loại.
Hiện tại, bạn Nam đã để dành được 500 nghìn đồng. Bạn Nam đang có ý định mua một máy tính hiệu Casio FX 580 với giá 800 nghìn đồng. Để thực hiện được điều trên, Nam đã lên kế hoạch mỗi ngày tiết kiệm 5 nghìn đồng. Gọi y (nghìn đồng) là số tiền bạn Nam tiết kiệm được sau x ngày theo kế hoạch.
a) Viết công thức biểu thị y theo x. Từ đó tính số tiền Nam tiết kiệm được theo kế hoạch sau 15 ngày.
b) Hỏi sau bao nhiêu ngày kể từ ngày bắt đầu tiết kiệm thì Nam có thể mua được cái máy tính đó?
Cho hình chóp S.ABCD có đáy là hình bình hành. Tìm các vectơ hiệu \[\overrightarrow {AS} - \overrightarrow {DC} \,;\,\,\overrightarrow {CS} - \overrightarrow {DA} .\]
Hình thang cân có tâm đối xứng không?
Hợp số lớn nhất có hai chữ số là gì?
Kết quả đo chiều dài của một thửa đất là 75,4 m ± 0,5 m và đo chiều dài của một cây cầu là 466,2 m ± 0,5 m. Các mệnh đề sau đúng hay sai:
a) Đối với phép đo thửa đất, sai số tương đối không vượt quá 0,663%.
b) Đối với phép đo thửa đất, có sai số tương đối: \[\frac{d}{{\left| a \right|}} = \frac{{0,5}}{{75,4}} = \frac{5}{{754}}\].
c) Đối với phép đo chiều dài cây cầu, có sai số tương đối lớn hơn \[\frac{5}{{4662}} \approx 0,107\% .\]
d) Phép đo cây cầu có độ chính xác cao hơn phép đo chiều dài của một thửa đất.
Cho hàm số \[y = 2x - 1 + \frac{3}{{x + 3}}\left( C \right).\] Khoảng cách từ điểm M(2; ‒1) đến tiệm cận xiên của đồ thị (C) là
\[\frac{2}{{\sqrt 5 }}.\]
\[\frac{4}{{\sqrt 5 }}.\]
2.
4.
Làm tròn số 25,0769 đến hàng phần trăm ta được kết quả là:
25,08.
25,07.
25,06.
25,09.
Tìm tập nghiệm S của phương trình \[{\log _{\sqrt 2 }}x + {\log _{\frac{1}{2}}}\left( {2x - 1} \right) = 2\] có dạng \[x = a + b\sqrt 3 \] (a, b là hai số nguyên). Giá trị của a + b bằng
6.
4.
10.
2.
Trong không gian Oxyz, cho hai điểm A(1; 2; ‒2), B(2; ‒1; 2). Tìm tọa độ điểm M trên mặt phẳng Oxy sao cho MA + MB đạt giá trị nhỏ nhất.
M(1; 1; 0).
\[M\left( {\frac{3}{2};\,\,\frac{1}{2};\,\,0} \right).\]
M(2; 1; 0).
\[M\left( {\frac{1}{2};\,\,\frac{3}{2};\,\,0} \right).\]
Một cầu thủ sút bóng đi theo quỹ đạo là một đường cong parabol có phương trình h(x) = ‒0,0083x2 + 0,1x + 3,1 với h(x) (được tính bằng mét) là độ cao của quả bóng so với mặt đất tại nơi cách vạch vôi khung thành một khoảng cách x mét. Tính khoảng cách từ vị trí đặt trái bóng đến vạch vôi khung thành (kết quả làm tròn đến hàng đơn vị).
Một chất điểm chuyển động với tốc độ được cho bởi hàm số \[v\left( t \right) = \left\{ \begin{array}{l}a\\{t^2} - 5t + 10\end{array} \right.\] khi \[\begin{array}{l}0 \le t \le 5\\t > 5\end{array}\], trong đó v(t) được tính theo đơn vị m/s và t được tính theo giây. Hỏi hàm v(t) có liên tục tại điểm t = 5 hay không?
Một doanh nghiệp sản xuất độc quyền một loại sản phẩm. Giả sử khi sản xuất và bán hết x sản phẩm (0 < x ≤ 2500), tổng số tiền doanh nghiệp thu được là f(x) = 2006x ‒ x2 và tổng chi phí là g(x) = x2 + 1438x ‒ 1209 (đơn vị: nghìn đồng). Giả sử mức thuế phụ thu trên một đơn vị sản phẩm bán được là t (nghìn đồng) (0 < t < 320). Giá trị của t bằng bao nhiêu nghìn đồng để nhà nước nhận số tiền thuế phụ thu lớn nhất và doanh nghiệp cũng nhận được lợi nhuận lớn nhất theo mức thuế phụ thu đó?
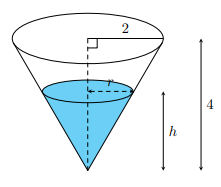
Một bể nước hình nón ngược với bán kính đáy bằng 2 m và chiều cao bằng 4 m (tham khảo hình vẽ dưới đây). Nước được bơm vào bể với tốc độ không đổi là 2 m3/phút. Hỏi tốc độ dâng lên của mực nước (đơn vị m/phút) bằng bao nhiêu khi mực nước trong bể đạt độ sâu bằng 3 m (làm tròn kết quả đến chữ số hàng phần trăm)?