Đề thi Học kì 1 Toán 10 - Bộ sách Kết nối tri thức - Đề 01
38 câu hỏi
Trong các phát biểu sau, phát biểu nào không phải là mệnh đề?
2 là số nguyên âm;
Bạn có thích học môn Toán không?
13 là số nguyên tố;
Số 15 chia hết cho 2.
Trong các tập hợp sau, tập hợp nào là tập con của tập hợp A = {1; 2; 3; 4; 5}?
A1 = {1; 6};
A2 = {0; 1; 3};
A3 = {4; 5};
A3 = {0}.
Cho các tập hợp A = {x ∈ ℝ| – 5 ≤ x < 1} và B = {x ∈ ℝ| – 3 < x ≤ 3}. Tìm tập hợp A ∪ B.
A ∪ B = [– 5; 1);
A ∪ B = [– 5; 3];
A ∪ B = (– 3; 1);
A ∪ B = (– 3; 3].
Trong các cặp số sau, cặp nào không là nghiệm của hệ bất phương trình \[\left\{ {\begin{array}{*{20}{c}}{x + y - 2 \le 0}\\{2x - 3y + 2 > 0}\end{array}} \right.\].
(0; 0);
(1; 1);
(– 1; 1);
(– 1; – 1).
Mệnh đề nào sau đây đúng?
sin (180° – α) = – sin α;
cos (180° – α) = – cos α;
tan (180° – α) = tan α;
cot (180° – α) = cot α.
Tam giác ABC có BC = 1, AC = 3, \(\widehat C = 60^\circ \). Tính độ dài cạnh AB.
\(\sqrt {13} \);
\(\frac{{\sqrt {46} }}{2}\);
\(\frac{{\sqrt {34} }}{2}\);
\(\sqrt 7 \).
Cho lục giác đều ABCDEF tâm O như hình vẽ bên. Vectơ \(\overrightarrow {OB} \) cùng phương với vectơ nào sau đây?

\(\overrightarrow {OC} \);
\(\overrightarrow {BC} \);
\(\overrightarrow {BE} \);
\(\overrightarrow {OA} \).
Mệnh đề nào sau đây sai:
\(\overrightarrow {MN} + \overrightarrow {NP} = \overrightarrow {MP} \);
\(\overrightarrow {MN} - \overrightarrow {MP} = \overrightarrow {PN} \);
\(\overrightarrow {MN} - \overrightarrow {NP} = \overrightarrow {MP} \);
\(\overrightarrow {MN} = \overrightarrow {IN} + \overrightarrow {MI} \).
Cho hình chữ nhật ABCD có AB = 4 cm, AD = 3 cm. Tính \(\left| {\overrightarrow {BC} + \overrightarrow {BA} } \right|\).
5 cm;
7 cm;
9 cm;
11 cm.
Cho G là trọng tâm của tam giác ABC và điểm M bất kỳ. Đẳng thức nào sau đây đúng?
\(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow {MG} \);
\(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 2\overrightarrow {MG} \);
\(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \);
\(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 4\overrightarrow {MG} \).
Cho ba điểm A, B, C như hình vẽ:

Đẳng thức nào sau đây đúng?
\(\overrightarrow {MB} = 3\overrightarrow {MA} \);
\(\overrightarrow {MB} = \frac{1}{3}\overrightarrow {AB} \);
\(\overrightarrow {AB} = 4\overrightarrow {MA} \);
\(\overrightarrow {MB} = - 3\overrightarrow {MA} \).
Trong mặt phẳng tọa độ Oxy, cho \(\overrightarrow u = - 2\overrightarrow i + \overrightarrow j \). Tìm tọa độ của vectơ \(\overrightarrow u \).
\(\overrightarrow u = \left( {2; - 1} \right)\);
\(\overrightarrow u = \left( { - 2;1} \right)\);
\(\overrightarrow u = \left( {2;1} \right)\);
\(\overrightarrow u = \left( { - 2; - 1} \right)\).
Trong mặt phẳng tọa độ, cặp vectơ nào sau đây cùng phương?
\(\overrightarrow a = \left( {1;0} \right)\) và \(\overrightarrow b = \left( {0;1} \right)\);
\(\overrightarrow u = \left( {3; - 2} \right)\) và \(\overrightarrow v = \left( {6;4} \right)\);
\(\overrightarrow i = \left( {2;3} \right)\) và \(\overrightarrow j = \left( { - 6; - 9} \right)\);
\(\overrightarrow c = \left( {2;3} \right)\) và \(\overrightarrow d = \left( { - 6;9} \right)\).
Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \)khác vectơ-không. Khẳng định nào sau đây là đúng?
\(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\sin \left( {\overrightarrow a ,\overrightarrow b } \right)\);
\(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\);
\(\overrightarrow a .\overrightarrow b = - \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\);
\(\overrightarrow a .\overrightarrow b = - \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\sin \left( {\overrightarrow a ,\overrightarrow b } \right)\).
Miền nghiệm của bất phương trình 2x – y + 6 ≤ 0 được biểu diễn là miền màu xanh trong hình ảnh nào sau đây ?
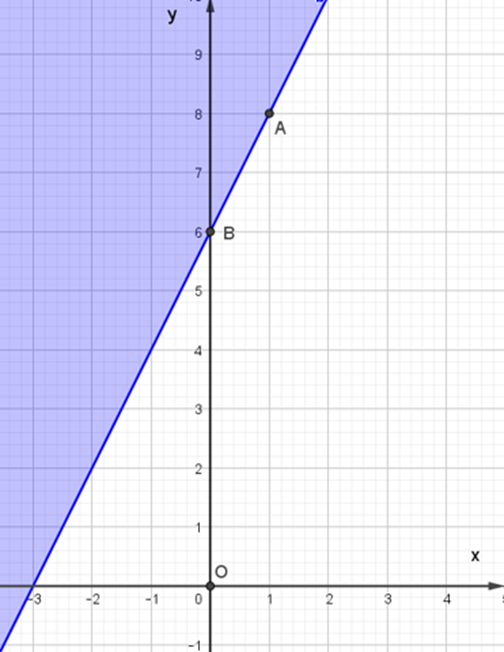
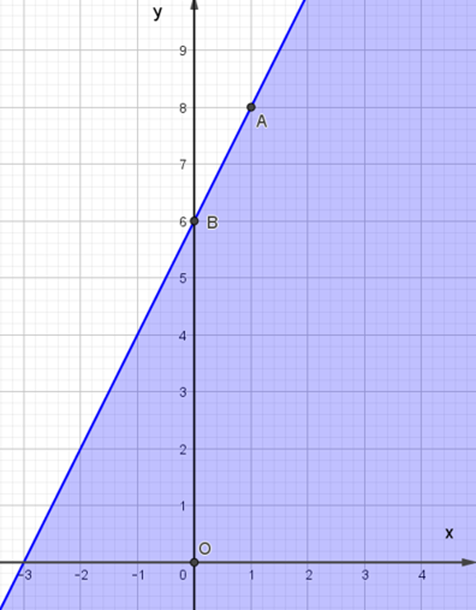
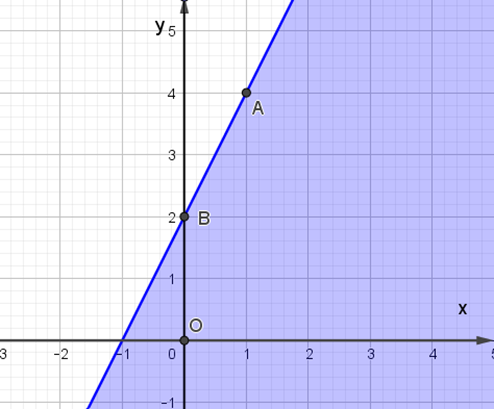
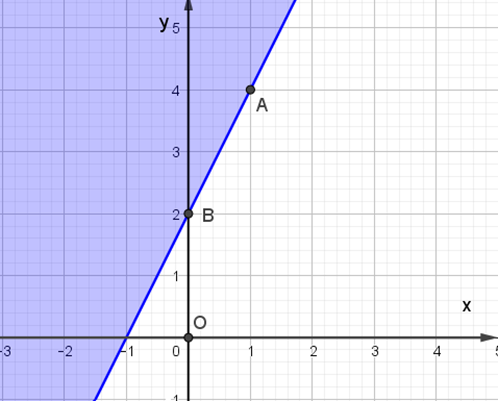
Cho tam giác ABC cân tại A có \[\widehat A = 120^\circ \]. Khi đó sin B bằng:
\(\frac{1}{2}\);
\( - \frac{1}{2}\);
\(\frac{{\sqrt 3 }}{2}\);
\( - \frac{{\sqrt 3 }}{2}\).
Cho góc α với 0° < α < 180°. Tính giá trị của cosα, biết \(\tan \alpha = - 2\sqrt 2 \).
\( - \frac{1}{3}\);
\(\frac{{2\sqrt 2 }}{3}\);
\(\frac{1}{3}\);
\(\frac{{\sqrt 2 }}{3}\).
Cho hình thoi ABCD. Vectơ – không có điểm đầu là A thì nó có điểm cuối là:
Điểm A;
Điểm B;
Điểm C;
Điểm D.
Cho tam giác ABC đều. Tính góc \(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right)\).
90°;
135°;
90°;
60°.
Cho tam giác ABC có: AB = 3, BC = 4, AC = 5. Tính \(\overrightarrow {BA} .\overrightarrow {BC} \).
1;
0;
12;
20.
Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) đều khác \(\overrightarrow 0 \). Biết: \(\left( {\overrightarrow a ,\overrightarrow b } \right) = 30^\circ \), \(\overrightarrow a .\overrightarrow b = \sqrt 3 \)và \(\left| {\overrightarrow b } \right| = 2\). Tính độ dài của vectơ \(\overrightarrow a \).
1;
2;
\(\frac{1}{2}\);
\(\frac{1}{4}\).
Một lực \(\overrightarrow F \) có độ lớn \(60\sqrt 3 \) N tác động vào điểm M làm vật di chuyển theo phương nằm ngang từ M đến điểm N cách M một khoảng 10 m. Biết góc giữa \(\overrightarrow F \) và phương thẳng đứng là 30°. Tính công sinh bởi lực F.
900 J;
800 J;
600 J;
\(300\sqrt 3 \)J.
Cho giá trị gần đúng của \(\sqrt 3 \) là 1,73. Sai số tuyệt đối của số gần đúng 1,73 là:
0,003;
0,03;
0,002;
0,02.
Viết số quy tròn của số gần đúng b biết \(\overline b \) = 12 409,12 ± 0,5.
12 410;
12 409,1;
12 000;
12 409.
Tính số trung bình của mẫu số liệu sau:
2; 5; 8; 7; 10; 20; 11.
8;
9;
10;
11.
Tìm trung vị của mẫu số liệu sau:
0; 1; 2; 3; 5; 9; 10.
3;
5;
0;
2.
Số lượng học sinh đăng kí thi môn cầu lông các lớp từ lớp 6 đến lớp 9 được thống kê trong bảng dưới đây:
Lớp | 6 | 7 | 8 | 9 |
Số lượng | 20 | 25 | 22 | 15 |
Tìm mốt trong mẫu số liệu trên.
6;
7;
8;
9.
Cho mẫu số liệu sau:
5; 2; 9; 10; 15; 5; 20.
Tứ phân vị Q1, Q2, Q3 của mẫu số liệu trên lần lượt là:
2; 5; 9;
5; 9; 15;
10; 5; 15;
2; 9; 15.
Cho mẫu số liệu sau:
12; 5; 8; 11; 6; 20; 22.
Tính khoảng biến thiên của mẫu số liệu trên.
16;
17;
18;
19.
Khoảng tứ phân vị ∆Q là
Q2 – Q1;
Q3 – Q1;
Q3 – Q2;
(Q1 + Q3) : 2.
Cho mẫu số liệu sau:
5; 6; 12; 2; 5; 17; 23; 15; 10.
Tính khoảng tứ phân vị của mẫu số liệu trên.
8;
9;
10;
11.
Cho mẫu số liệu sau:
10; 3; 6; 9; 15.
Tìm độ lệch chuẩn của mẫu số liệu trên (làm tròn đến hàng phần trăm).
3,03;
4,03;
5,03;
6,03.
Cho tam giác đều ABC cạnh 4. Vectơ \( - \frac{1}{2}\overrightarrow {BC} \) có độ dài là.
2;
4;
3;
6.
Cho hình bình hành ABCD. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh AB và CD sao cho AB = 3AM, CD = 2CN. Biểu diễn vectơ \(\overrightarrow {AN} \) qua các vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \).
\(\overrightarrow {AN} \) = \( - \overrightarrow {AC} + \frac{1}{2}\overrightarrow {AB} \);
\(\overrightarrow {AN} \) = \(\overrightarrow {AC} + \frac{1}{2}\overrightarrow {AB} \);
\(\overrightarrow {AN} \) = \( - \overrightarrow {AC} - \frac{1}{2}\overrightarrow {AB} \);
\(\overrightarrow {AN} \) = \(\overrightarrow {AC} - \frac{1}{2}\overrightarrow {AB} \).
Trong mặt phẳng tọa độ Oxy cho ba điểm A(2; 1), B(1; 10) và điểm C(m; 2m – 17). Tất cả các giá trị của tham số m sao cho AB vuông góc với OC là
m = 9;
m = ±9;
m = – 9;
m = 1.
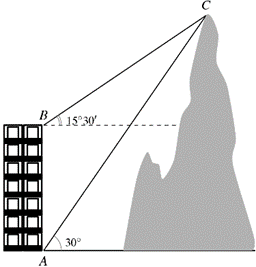
Từ hai vị trí A và B của một tòa nhà, người ta quan sát đỉnh C của ngọn núi. Biết rằng độ cao AB = 70 m, phương nhìn AC tạo với phương nằm ngang góc 30°, phương nhìn BC tạo với phương nằm ngang góc 15°30'. Ngọn núi đó có độ cao so với mặt đất là bao nhiêu (làm tròn đến hàng phần trăm)?
Cho tam giác đều ABC có độ dài cạnh bằng a. Trên các cạnh BC, CA, AB lần lượt lấy các điểm N, M, P sao cho \(BN = \frac{a}{3},CM = \frac{{2a}}{3},AP = x\left( {0 < x < a} \right)\). Tìm giá trị của x theo a để đường thẳng AN vuông góc với đường thẳng PM.
Một cảnh sát giao thông ghi lại tốc độ (đơn vị: km/h) của 25 xe qua trạm như sau:
20 | 41 | 41 | 80 | 40 | 52 | 52 | 52 | 60 | 55 | 60 | 60 | 62 |
60 | 55 | 60 | 55 | 90 | 70 | 35 | 40 | 30 | 30 | 80 | 25 |
|
Tìm các số liệu bất thường (nếu có) trong mẫu số liệu trên.








