Bộ 10 đề thi cuối kì 1 Toán 10 Kết nối tri thức có đáp án - Đề 3
38 câu hỏi
I. Trắc nghiệm (7 điểm)
Trong các phát biểu sau, phát biểu nào là mệnh đề đúng?
“\(\pi \)là một số hữu tỉ.”;
“Tổng của hai cạnh một tam giác lớn hơn cạnh thứ ba.”;
“Bạn có chăm học không?”;
“Con thì thấp hơn cha.”.
Trong các tập hợp sau, tập nào có đúng một tập hợp con ?
\(\emptyset \);
\(\left\{ 1 \right\}\);
\(\left\{ {1;\,\,2;\,\,3} \right\}\);
\(\left\{ {1;\,\,2} \right\}\).
Cho hai tập hợp \[A = \left\{ {x \in \mathbb{R}\left| {2{x^2} - 3x + 1 = 0} \right.} \right\},B = \left\{ {x \in {\mathbb{N}^*}\left| {3x - 2 < 10} \right.} \right\}\], khi đó:
\(A\backslash B = \left\{ {\frac{1}{2};\,\,1;\,\,2;\,\,3} \right\}\);
\(A\backslash B = \left\{ {\frac{1}{2};\,\,1} \right\}\);
\(A\backslash B = \left\{ {\frac{1}{2}} \right\}\);
\(A\backslash B = \left\{ {2;\,\,3} \right\}\).
Nửa mặt phẳng không bị gạch chéo ở hình dưới đây là miền nghiệm của bất phương trình nào trong các bất phương trình sau?
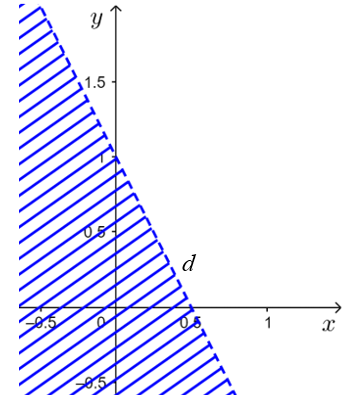
\(x + 2y > 1\);
\(2x + y > 1\);
\(2x + y < 1\);
\(2x - y > 1\).
Trong các hệ bất phương trình sau, hệ bất phương trình nào là hệ bất phương trình bậc nhất hai ẩn?
\(x - y > 0\);
\[\left\{ {\begin{array}{*{20}{c}}{{x^2} - 4 \ge 0}\\{3x + 4y < 2}\end{array}} \right.\];
\[\left\{ {\begin{array}{*{20}{c}}{{y^2} + 2y - 3 > 0}\\{5x - y > 2}\end{array}} \right.\];
\[\left\{ {\begin{array}{*{20}{c}}{x - 4 \ge y}\\{3x + 4y < 2}\end{array}} \right.\].
Giá trị của \(\tan 45^\circ + \cot 135^\circ \) bằng bao nhiêu?
0;
\(\sqrt 3 \);
1;
2.
Khẳng định nào sau đây là đúng với \(0^\circ < \alpha < 180^\circ \)?
\(\sin \alpha = - \sin \left( {180^\circ - \alpha } \right)\);
\(\cos \alpha = - \cos \left( {180^\circ - \alpha } \right)\);
\(\tan \alpha = \tan \left( {180^\circ - \alpha } \right)\);
\(\cot \alpha = \cot \left( {180^\circ - \alpha } \right)\).
Giá trị của biểu thức \(A = \tan 1^\circ \cdot \tan 2^\circ \cdot \tan 3^\circ ...\tan 88^\circ \cdot \tan 89^\circ \) là
– 1;
1;
0;
3.
Cho \(\Delta ABC\) có \(AB = 6;\,BC = 8;\,\widehat B = 60^\circ \). Tính độ dài cạnh \(AC\).
\(3\sqrt {12} \);
\(2\sqrt {13} \);
\(2\sqrt {37} \);
\(2\sqrt 5 \).
Chọn khẳng định đúng trong các khẳng định sau:
Vectơ là một đường thẳng có hướng;
Vectơ là một đoạn thẳng;
Vectơ là một đoạn thẳng có hướng;
Vectơ là một đoạn thẳng không phân biệt điểm đầu và điểm cuối.
Cho hình lục giác đều \(ABCDEF\) tâm \(O\). Số các vectơ khác vectơ-không, cùng phương với vectơ \(\overrightarrow {OD} \) có điểm đầu và điểm cuối là các đỉnh của lục giác là
4;
6;
8;
10.
Cho hình bình hành \(ABCD\), với giao điểm hai đường chéo là \(I\). Khi đó:
\(\overrightarrow {AB} + \overrightarrow {IA} = \overrightarrow {BI} \);
\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {BD} \);
\(\overrightarrow {AB} + \overrightarrow {CD} = \vec 0\);
\(\overrightarrow {AB} + \overrightarrow {BD} = \vec 0\).
Cho 4 điểm bất kì \(A,\,B,\,C,\,O\). Đẳng thức nào sau đây đúng?
\[\overrightarrow {OA} = \overrightarrow {OB} - \overrightarrow {BA} \];
\[\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {AO} \];
\[\overrightarrow {AB} = \overrightarrow {AC} - \overrightarrow {CB} \];
\[\overrightarrow {OA} = \overrightarrow {CA} - \overrightarrow {CO} \].
Gọi \[G\] là trọng tâm tam giác vuông \[ABC\;\] với cạnh huyền \[BC = 12\]. Vectơ \[\overrightarrow {GB} - \overrightarrow {CG} \] có độ dài bằng
2;
4;
8;
\(2\sqrt 3 \).
Cho tam giác \[ABC\] với trung tuyến \[AM\] và trọng tâm \[G\]. Khi đó \[\overrightarrow {GA} = \]
\(2\overrightarrow {GM} \);
\(\frac{2}{3}\overrightarrow {GM} \);
\( - \frac{2}{3}\overrightarrow {AM} \);
\(\frac{1}{2}\overrightarrow {AM} \).
Giá trị của \(k\) sao cho \(\overrightarrow a = k\overrightarrow b \), biết rằng \(\overrightarrow a ,\,\overrightarrow b \) cùng hướngvà \(\left| {\overrightarrow a } \right| = 2,\,\,\left| {\overrightarrow b } \right| = 4\) là
\(k = 2\);
\(k = - 2\);
\(k = \frac{1}{2}\);
\(k = - \frac{1}{2}\).
Cho tam giác \[ABC\] có điểm \[M\]thuộc cạnh \[BC\] sao cho \[CM = 2MB\] và \[I\] là trung điểm của \[AB\]. Đẳng thức nào sau đây đúng?
\[\overrightarrow {IM} = \frac{1}{6}\overrightarrow {AB} - \frac{1}{3}\overrightarrow {AC} \];
\[\overrightarrow {IM} = \frac{1}{6}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \];
\[\overrightarrow {IM} = \frac{1}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \];
\[\overrightarrow {IM} = \frac{1}{3}\overrightarrow {AB} + \frac{1}{6}\overrightarrow {AC} \].
Đẳng thức nào sau đây mô tả đúng hình vẽ dưới?

\[3\overrightarrow {AI} + \overrightarrow {AB} = \overrightarrow 0 \];
\[3\overrightarrow {IA} + \overrightarrow {IB} = \overrightarrow 0 \];
\[\overrightarrow {BI} + 3\overrightarrow {BA} = \overrightarrow 0 \];
\[\overrightarrow {AI} + 3\overrightarrow {AB} = \overrightarrow 0 \].
Trong mặt phẳng tọa độ \[Oxy\], cho vectơ \(\overrightarrow u = - \,4\overrightarrow i - 9\overrightarrow j \). Tọa độ của vectơ \(\overrightarrow u \) là
\(\overrightarrow u = \left( {4;\, - 9} \right)\);
\(\overrightarrow u = \left( {4;\,9} \right)\);
\(\overrightarrow u = \left( { - \,4;\, - 9} \right)\);
\(\overrightarrow u = \left( { - 4;\,9} \right)\).
Trong mặt phẳng tọa độ \(Oxy\), cho hai điểm \(M\left( {2;\,\, - 3} \right)\) và \(N\left( { - 1;\, - 5} \right)\). Tọa độ của vectơ \(\overrightarrow {NM} \) là
\(\overrightarrow {NM} = \left( { - 3;\,\, - 2} \right)\);
\(\overrightarrow {NM} = \left( {3;\,\,2} \right)\);
\(\overrightarrow {NM} = \left( {3;\, - 2} \right)\);
\(\overrightarrow {NM} = \left( { - 3;\,\,2} \right)\).
Trong mặt phẳng tọa độ \(Oxy\) cho bốn điểm \[A\left( {3; - 2} \right)\], \[B\left( {7;\,\,1} \right)\], \[C\left( {0;\,\,1} \right)\], \[D\left( { - 8; - 5} \right)\]. Khẳng định nào sau đây là đúng?
Hai vectơ \(\overrightarrow {AB} ,\,\,\overrightarrow {CD} \) đối nhau;
Hai vectơ \(\overrightarrow {AB} ,\,\,\overrightarrow {CD} \) cùng phương, ngược hướng;
Hai vectơ \(\overrightarrow {AB} ,\,\,\overrightarrow {CD} \) cùng phương, cùng hướng;
Hai vectơ \(\overrightarrow {AB} ,\,\,\overrightarrow {CD} \) không cùng phương.
Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) khác vectơ \(\overrightarrow 0 \).Tích vô hướng của hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) là một số thực được xác định bởi
\(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot \sin \left( {\overrightarrow a ,\,\overrightarrow b } \right)\);
\(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot \cos \left( {\overrightarrow a ,\,\overrightarrow b } \right)\);
\(\overrightarrow a \cdot \overrightarrow b = - \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot \sin \left( {\overrightarrow a ,\,\overrightarrow b } \right)\);
\(\overrightarrow a \cdot \overrightarrow b = - \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot \cos \left( {\overrightarrow a ,\,\overrightarrow b } \right)\).
Cho \(\overrightarrow a \) và \(\overrightarrow b \) là hai vectơ vuông góc với nhau. Mệnh đề nào sau đây đúng?
\(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right|\);
\(\overrightarrow a \cdot \overrightarrow b = 0\);
\(\overrightarrow a \cdot \overrightarrow b = - 1\);
\(\overrightarrow a \cdot \overrightarrow b = - \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right|\).
Cho các vectơ \(\overrightarrow a = \left( {1; - 2} \right),\,\,\overrightarrow b = \left( { - 2; - 6} \right)\). Khi đó góc giữa chúng là
\(45^\circ \);
\(60^\circ \);
\(30^\circ \);
\(135^\circ \).
Cho tam giác \(ABC\) có \(AB = 1\), \(BC = 2\) và \(\widehat {ABC} = 60^\circ \). Tích vô hướng \(\overrightarrow {BC} \cdot \overrightarrow {CA} \) bằng
\(\sqrt 3 \);
\( - \sqrt 3 \);
\(3\);
\( - 3\).
Số quy tròn của số gần đúng \(a\) trong trường hợp là
55 000;
54 880;
54 890;
54 900.
Làm tròn số 23,87 đến hàng phần mười. Sai số tuyệt đối của số quy tròn là
0,01;
0,02;
0,03;
Đáp án khác.
Các giá trị xuất hiện nhiều nhất trong mẫu số liệu được gọi là
Phương sai;
Số trung bình;
Mốt;
Số trung vị.
Có 100 học sinh tham dự kì thi học sinh giỏi môn Toán (thang điểm 20). Kết quả như sau:
Điểm | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
Tần số | 1 | 1 | 3 | 5 | 8 | 13 | 19 | 24 | 14 | 10 | 2 |
Giá trị mốt của mẫu số liệu trên là
1;
24;
16;
10.
Cân nặng của một nhóm gồm 10 học sinh lớp 10 (đơn vị: kg) lần lượt là 50; 46; 48; 59; 48; 47; 56; 59; 57; 40. Cân nặng trung bình của cả nhóm là
40,3;
48;
49;
50.
Trung vị của mẫu số liệu trong Câu 30 là
40,3;
48;
49;
50.
Khoảng tứ phân vị \({\Delta _Q}\) là
\({Q_2} - {Q_1}\);
\({Q_3} - {Q_2}\);
\({Q_3} - {Q_1}\);
\({Q_2} - {Q_3}\).
Số quả cam được hái từ 9 cây cam trong vườn lần lượt là: 100; 200; 150; 145; 145; 154; 166; 167; 101. Khoảng biến thiên của mẫu số liệu trên là
100;
101;
102;
103.
Phương sai của mẫu số liệu trong Câu 33 xấp xỉ bằng
884,26;
884,25;
884,24;
884,23.
Khoảng tứ phân vị của mẫu số liệu ở Câu 33 là
33;
16,5;
45,3;
43,5.
II. Tự luận (3 điểm)
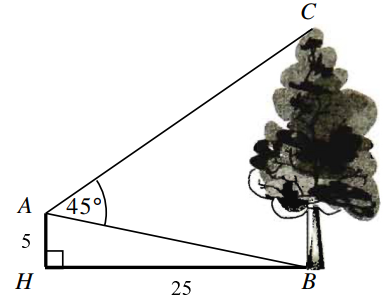
(1 điểm) Từ vị trí \(A\), người ta quan sát một cây cao (như hình dưới). Biết \(AH = 5\,\,{\rm{m,}}\)\(HB = 25\,{\rm{m}}\), \(\widehat {BAC} = 45^\circ \). Tính chiều cao \(BC\) của cây.
(1 điểm) Cho tam giác \(ABC\) có \[BC = a,\,\,CA = b,\,\,AB = c\]. Gọi \(M\) là trung điểm của\(BC\), \(D\) là chân đường phân giác trong góc \(A\). Tính \[{\overrightarrow {AD} ^2}\] theo \(a,\,\,b,\,\,c\).
(1 điểm) Cho mẫu số liệu sau:
20 25 20 30 33 40 38 25 22 90
Tìm các giá trị bất thường (nếu có) của mẫu số liệu trên.








