Bộ 10 đề thi cuối kì 1 Toán 10 Kết nối tri thức có đáp án - Đề 2
38 câu hỏi
I. Trắc nghiệm (7 điểm)
Trong các câu sau, câu nào không phải là mệnh đề?
“Năm 2024 là năm nhuận.”;
“Số 2 022 là số lẻ.”;
“Số 25 là số chính phương.”;
“Hà có học giỏi môn Toán không?”.
Cho tập hợp \(H = \left\{ {{x^2}|x \in \mathbb{N},x \le 4} \right\}\). Viết tập hợp \(H\) bằng cách liệt kê các phần tử ta được
\(H = \left\{ {0;\,\,1;\,\,2;\,\,3;\,\,4} \right\}\);
\(H = \left\{ {0;\,\,1;\,\,4;\,\,9;\,\,16} \right\}\);
\(H = \left\{ {0;\,\,2;\,\,4;\,\,6;\,\,8} \right\}\);
Cho hai tập hợp: \(A = \left( { - 2;\,\,9} \right),B = \left[ { - 3;\,\,5} \right]\). Khi đó \(A \cap B\) là tập hợp nào sau đây?
\(\left[ { - 2;\,\, - 3} \right]\);
\(\left( { - 2;\,\,5} \right)\);
\(\left( { - 2;\,\,5} \right]\);
\(\left[ { - 2;\,\,5} \right]\).
Phần không tô đậm trong hình vẽ (kể cả đường thẳng \(\Delta \)) biểu diễn tập nghiệm của bất phương trình nào trong các bất phương trình sau?
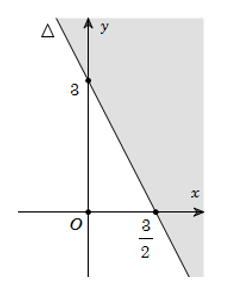
\(x + 2y \le 3\);
\(x + 2y \ge 3\);
\(2x + y \le 3\);
\(2x + y \ge 3\).
Người ta dự định dùng hai nguyên liệu là mía và củ cải đường để chiết xuất ít nhất 140 kg đường kính và 9 kg đường cát. Từ mỗi tấn mía có thể chiết xuất được 20 kg đường kính và 0,6 kg đường cát. Từ mỗi tấn củ cải đường có thể chiết xuất được 10 kg đường kính và 1,5 kg đường cát. Gọi số tấn mía cần dùng là \(x\) và số tấn củ cải đường cần dùng là \(y\). Biết rằng cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 10 tấn mía và không quá 9 tấn củ cải đường. Một hệ điều kiện giữa \(x\) và \(y\) thỏa mãn yêu cầu bài toán là
\(\left\{ \begin{array}{l}0 \le x \le 10\\0 \le y \le 9\\20x + 10y \le 140\\0,6x + 1,5y \le 9\end{array} \right.\);
\(\left\{ \begin{array}{l}0 \le x \le 10\\0 \le y \le 9\\20x + 10y > 140\\0,6x + 1,5y > 9\end{array} \right.\);
\(\left\{ \begin{array}{l}x > 0\\y > 0\\20x + 10y \ge 140\\0,6x + 1,5y \ge 9\end{array} \right.\);
\(\left\{ \begin{array}{l}0 \le x \le 10\\0 \le y \le 9\\20x + 10y \ge 140\\0,6x + 1,5y \ge 9\end{array} \right.\).
Giá trị của \(\cos 150^\circ \) là
một số hữu tỉ âm;
một số hữu tỉ dương;
một số thực dương;
một số thực âm.
Cho góc \(\alpha \) thỏa mãn \(0^\circ < \alpha < 90^\circ \). Khẳng định nào sau đây sai?
\({\rm{sin}}\alpha \) và \(\cot \alpha \) cùng dấu;
Tích \({\rm{sin}}\alpha \cdot {\rm{cot}}\alpha \) mang dấu âm;
Tích \({\rm{sin}}\alpha \cdot {\rm{cos}}\alpha \) mang dấu dương;
\({\rm{sin}}\alpha \) và \(\tan \alpha \) cùng dấu.
Giá trị của biểu thức \(A = {\sin ^2}52^\circ + {\sin ^2}47^\circ + {\sin ^2}38^\circ + {\sin ^2}43^\circ \) là
– 1;
1;
0;
2.
Cho \(\Delta ABC\) có \(AB = 3;\,BC = 7;\,AC = 5\). Số đo góc \(A\) là
\(30^\circ \);
\(60^\circ \);
\(120^\circ \);
\(150^\circ \).
Cho tứ giác \(ABCD\), số các vectơ khác vectơ-không có điểm đầu và điểm cuối là đỉnh của tứ giác là
4;
6;
8;
12.
Cho ba điểm \(H,\,I,\,K\) thẳng hàng, trong đó điểm \(I\) nằm giữa hai điểm \(H\) và \(K\). Khi đó cặp vectơ nào sau đây cùng hướng?
\(\overrightarrow {HI} \) và \(\overrightarrow {KH} \);
\(\overrightarrow {HI} \) và \(\overrightarrow {IK} \);
\(\overrightarrow {HK} \) và \(\overrightarrow {KI} \);
\(\overrightarrow {IK} \) và \(\overrightarrow {IH} \).
Cho ba điểm phân biệt A,B,C. Trong các khẳng định sau, khẳng định nào sai?
\[\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \];
\[\overrightarrow {AC} + \overrightarrow {CB} = \overrightarrow {AB} \];
\[\overrightarrow {CA} + \overrightarrow {BC} = \overrightarrow {BA} \];
\[\overrightarrow {CB} + \overrightarrow {AC} = \overrightarrow {BA} \].
Gọi \(O\) là tâm hình bình hành \(ABCD\). Hỏi vectơ \(\overrightarrow {AO} - \overrightarrow {DO} \) bằng vectơ nào?
\(\overrightarrow {BA} \);
\(\overrightarrow {BC} \);
\(\overrightarrow {DC} \);
\(\overrightarrow {AC} \).
Cho đoạn thẳng \(AB\), \(M\) là điểm thỏa \[\overrightarrow {MA} + \overrightarrow {BA} = \overrightarrow 0 \]. Mệnh đề nào sau đây đúng?
\(M\)là trung điểm \(AB\);
\(M\)trùng \(A\);
\(M\)trùng\(B\);
\(A\) là trung điểm \(MB\).
Cho \(G\) là trọng tâm của tam giác \(ABC\). Với mọi điểm \(M\)ta luôn có:
\(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow {MG} \);
\(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 2\overrightarrow {MG} \);
\(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \);
\(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 4\overrightarrow {MG} \).
Cho vectơ \(\overrightarrow a \ne \overrightarrow 0 \) và điểm \(O\). Gọi \(M,N\) lần lượt là hai điểm thỏa mãn \(\overrightarrow {OM} = 3\overrightarrow a \) và \(\overrightarrow {ON} = - 4\overrightarrow a \). Khi đó:
\(\overrightarrow {MN} = 7\overrightarrow a \);
\(\overrightarrow {MN} = - 5\overrightarrow a \);
\(\overrightarrow {MN} = - 7\overrightarrow a \);
\(\overrightarrow {MN} = - 5\overrightarrow a \).
Trên đường thẳng chứa cạnh \(BC\) của tam giác \(ABC\) lấy một điểm \(M\) sao cho \(\overrightarrow {MB} = 3\overrightarrow {MC} \). Khi đó đẳng thức nào sau đây đúng?
\(\overrightarrow {AM} = - \frac{1}{2}\overrightarrow {AB} + \frac{3}{2}\overrightarrow {AC} \);
\(\overrightarrow {AM} = 2\overrightarrow {AB} + \overrightarrow {AC} \);
\(\overrightarrow {AM} = \overrightarrow {AB} - \overrightarrow {AC} \);
\[\overrightarrow {AM} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\].
Trên đường thẳng \(MN\) lấy điểm \(P\) sao cho \(\overrightarrow {MN} = - 3\overrightarrow {MP} \). Điểm \(P\) được xác định đúng trong hình vẽ nào sau đây?
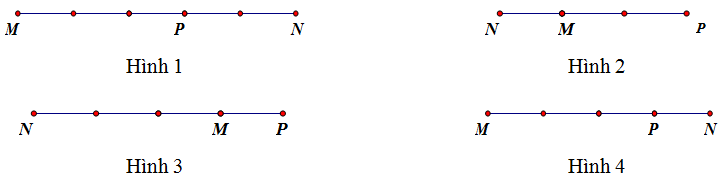
Hình 1;
Hình 2;
Hình 3;
Hình 4.
Trong mặt phẳng tọa độ \[Oxy\], cho vectơ \(\overrightarrow v = - 7\overrightarrow i + 8\overrightarrow j \). Tọa độ của vectơ \(\overrightarrow v \) là
\(\overrightarrow v = \left( {7;\, - 8} \right)\);
\(\overrightarrow v = \left( {7;\,8} \right)\);
\(\overrightarrow v = \left( { - 7;\, - 8} \right)\);
\(\overrightarrow v = \left( { - 7;\,8} \right)\).
Trong mặt phẳng tọa độ \(Oxy\), cho hai điểm \(A\left( {2;\,\, - 3} \right)\) và \(B\left( { - 5;\, - 4} \right)\). Tọa độ của vectơ \(\overrightarrow {BA} \) là
\(\overrightarrow {BA} = \left( {7;\,\,1} \right)\);
\(\overrightarrow {BA} = \left( { - 7;\,\, - 1} \right)\);
\(\overrightarrow {BA} = \left( {7;\, - 1} \right)\);
\(\overrightarrow {BA} = \left( { - 7;\,1} \right)\).
Cho tam giác \(ABC\) có \(A\left( {6;{\rm{ }}1} \right),{\rm{ }}B\left( { - 3;{\rm{ }}5} \right)\) và trọng tâm \(G\left( { - 1;{\rm{ }}1} \right)\). Tìm tọa độ đỉnh \(C\).
\(\left( {6;\, - 3} \right)\);
\(\left( { - 6;\,\,3} \right)\);
\(\left( { - 6;\, - 3} \right)\);
\(\left( { - 3;\,\,6} \right)\).
Cho \(\overrightarrow a \) và \(\overrightarrow b \) là hai vectơ ngược hướng và đều khác vectơ \(\overrightarrow 0 \). Mệnh đề nào sau đây đúng?
\(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right|\);
\(\overrightarrow a \cdot \overrightarrow b = - 1\);
\(\overrightarrow a \cdot \overrightarrow b = - \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right|\).
Cho hai điểm \(A\left( {2;\,2} \right)\) và \(B\left( {5;\, - 2} \right)\). Tìm điểm \(M\) nằm trên tia \[Ox\] sao cho \(\widehat {AMB} = 90^\circ \).
\(M\left( {1;\,\,6} \right)\);
\(M\left( {6;\,\,0} \right)\);
\(M\left( {1;\,\,0} \right)\) hoặc \(M\left( {6;\,\,0} \right)\);
\(M\left( {0;\,\,1} \right)\).
Cho các vectơ \(\overrightarrow a = \left( {1;\, - 3} \right)\) và \(\overrightarrow b = \left( {2;\,5} \right)\). Tích vô hướng của \(\overrightarrow a \cdot \left( {\overrightarrow a + 2\overrightarrow b } \right)\) bằng
16;
26;
36;
– 16.
Cho tam giác \(ABC\) vuông tại \(A\) có \(\widehat {ABC} = 50^\circ \). Hệ thức nào sau đây sai?
\(\left( {\overrightarrow {BA} ,\,\overrightarrow {BC} } \right) = 50^\circ \);
\(\left( {\overrightarrow {CA} ,\,\overrightarrow {CB} } \right) = 40^\circ \);
\(\left( {\overrightarrow {AB} ,\,\overrightarrow {CB} } \right) = 50^\circ \);
\(\left( {\overrightarrow {AC} ,\,\overrightarrow {CB} } \right) = 120^\circ \).
Số quy tròn của số gần đúng \(a\) trong trường hợp \(\overline a = 13,738 \pm 0,02\) là
13,738;
13,7;
13,8;
13,74.
Làm tròn số 152,559 đến hàng phần trăm. Sai số tuyệt đối của số quy tròn là
0,001;
0,01;
0,1;
Đáp án khác.
Số đặc trưng nào sau đây đo xu thế trung tâm của mẫu số liệu?
Khoảng biến thiên;
Độ lệch chuẩn;
Khoảng tứ phân vị;
Số trung bình.
Cho bảng thống kê sau
Giá trị | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Tần số | 18 | 15 | 20 | 32 | 40 | 18 | 15 |
Giá trị mốt của mẫu số liệu trên là
40;
5;
15;
18.
Thu nhập hằng tháng của 9 nhân viên trong một công ty luật lần lượt là 10; 12; 9; 11; 15; 18; 16; 9; 8. Thu nhập trung bình của 9 nhân viên đó là
11;
12;
13;
14.
Trung vị của mẫu số liệu trong Câu 30 là
10;
11;
11,5;
12.
Để đánh giá mức độ phân tán của mẫu số liệu thống kê, ta dùng đại lượng nào sau đây?
Số trung vị;
Số trung bình;
Tứ phân vị;
Độ lệch chuẩn.
Cho mẫu số liệu sau: 15; 12; 17; 14; 17; 12; 15; 17; 15; 18. Khoảng biến thiên của mẫu số liệu trên là
6;
3;
12;
18.
Độ lệch chuẩn trong mẫu số liệu ở Câu 33 là
1,98;
1,99;
\(\frac{{3\sqrt {11} }}{5}\);
2.
Khoảng tứ phân vị của mẫu số liệu ở Câu 33 là
2;
3;
2,75;
6.
II. Tự luận (3 điểm)
(1 điểm) Để làm đường điện dây cao thế ở Hà Giang từ vị trí bản \(A\) đến bản \(B\), người ta phải tránh một ngọn núi nên người ta phải nối thẳng đường dây từ bản \(A\) đến bản \(C\) dài 12 km rồi nối từ bản \(C\) đến bản \(B\) dài 8 km. Qua đo đạc người ta xác định được \(\widehat {ABC} = 65^\circ \). Hỏi so với việc nối thẳng từ bản \(A\) đến bản \(B\), người ta tốn thêm bao nhiêu tiền, biết mỗi km dây có giá 150 000 đồng.
(1 điểm) Trên mặt phẳng tọa độ \(Oxy\), cho \(\overrightarrow a = \left( {2 + x; - 3} \right)\) và \(\overrightarrow b = \left( {1;\,\,2} \right)\). Đặt \(\overrightarrow u = 2\overrightarrow a + \overrightarrow b \). Gọi \(\overrightarrow v = \left( { - 5;\,\,8} \right)\) là vectơ ngược hướng với vectơ \(\overrightarrow u \). Tìm \(x\) biết \(\left| {\overrightarrow v } \right| = 2\left| {\overrightarrow u } \right|\).
(1 điểm) Bạn Nam dùng đồng hồ bấm giờ để đo thời gian một vật rơi tự do (đơn vị: giây) từ tầng năm của một tòa nhà xuống mặt đất trong 10 lần cho kết quả như sau:
0,899; 0,898; 0,895; 0,901; 0,898; 0,902; 0,910; 0,312; 0,905; 0,899.
Nam nghĩa rằng giá trị 0,312 ở lần đo thứ 8 không chính xác. Hãy kiểm tra nghi ngờ của Nam.








