Bộ 10 đề thi cuối kì 1 Toán 10 Kết nối tri thức có đáp án - Đề 1
38 câu hỏi
I. Trắc nghiệm (7 điểm)
Trong các câu sau, câu nào không phải là mệnh đề?
Bạn ăn tối chưa?;
Hình vuông có hai đường chéo vuông góc với nhau;
7 không phải là số chính phương;
Bắc Kinh là thủ đô của Thái Lan.
Cách viết nào sau đây là đúng?
\(a \subset \left[ {a;\,b} \right]\);
\(\left\{ a \right\} \subset \left[ {a;\,b} \right]\);
\(\left\{ a \right\} \in \left[ {a;\,b} \right]\);
\(a \in \left( {a;\,b} \right]\).
Cho hai tập hợp: \(A = \left\{ {0;\,1;\,2;\,3;\,4} \right\},B = \left\{ {1;\,3;\,4;\,6;\,8} \right\}\). Trong các mệnh đề sau, mệnh đề nào đúng?
\(A \cap B = B\);
\(A \cup B = A\);
\(A\backslash B = \left\{ {0;\,2} \right\}\);
\(B\backslash A = \left\{ {0;\,4} \right\}\).
Phần không tô đậm trong hình vẽ biểu diễn tập nghiệm của bất phương trình nào trong các bất phương trình sau?
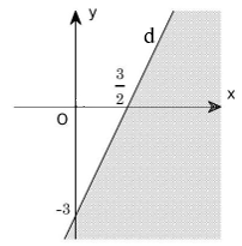
\(x - 2y < 3\);
\(x - 2y > 3\);
\(2x - y > 3\);
\(2x - y < 3\).
Một xưởng sản xuất hai loại sản phẩm, mỗi kg sản phẩm loại một cần \(2{\rm{\;kg}}\) nguyên liệu và 30 giờ, đem lại mức lợi nhuận 40 000 đồng. Mỗi sản phẩm loại hai cần \(4{\rm{\;kg}}\) nguyên liệu và 15 giờ đem lại mức lợi nhuận là 30 000 đồng. Xưởng có \(200{\rm{\;kg}}\) nguyên liệu và 1 200 giờ làm việc. Gọi \(x\left( {x \ge 0} \right)\) là số kg sản phẩm loại một cần sản xuất, \(y\left( {y \ge 0} \right)\) là số kg sản phẩm loại hai cần sản xuất. Một hệ điều kiện giữa \(x\) và \(y\) thỏa mãn yêu cầu bài toán là
\(\left\{ {\begin{array}{*{20}{l}}{x + 2y - 100 \le 0}\\{2x + y - 80 \le 0}\\{x \ge 0}\\{y \ge 0}\end{array}} \right.\);
\(\left\{ {\begin{array}{*{20}{l}}{x + 2y - 100 < 0}\\{2x + y - 80 < 0}\\{x \ge 0}\\{y \ge 0}\end{array}} \right.\);
\(\left\{ {\begin{array}{*{20}{l}}{x + 2y - 100 \ge 0}\\{2x + y - 80 \ge 0}\\{x \ge 0}\\{y \ge 0}\end{array}} \right.\);
\(\left\{ {\begin{array}{*{20}{l}}{x + 2y - 100 > 0}\\{2x + y - 80 > 0}\\{x \ge 0}\\{y \ge 0}\end{array}} \right.\).
Giá trị của \(\cos 60^\circ + \sin 30^\circ \) bằng bao nhiêu?
\(\frac{{\sqrt 3 }}{2}\);
\(\sqrt 3 \);
\(\frac{{\sqrt 3 }}{3}\);
1.
Cho góc \(\alpha \) thỏa mãn \(90^\circ < \alpha < 180^\circ \). Khẳng định nào sau đây đúng?
\({\rm{sin}}\alpha \) và \(\cot \alpha \) cùng dấu;
Tích \({\rm{sin}}\alpha \cdot {\rm{cot}}\alpha \) mang dấu âm;
Tích \({\rm{sin}}\alpha \cdot {\rm{cos}}\alpha \) mang dấu dương;
\({\rm{sin}}\alpha \) và \(\tan \alpha \) cùng dấu.
Giá trị của biểu thức \(H = \cos 0^\circ + \cos 10^\circ + \cos 20^\circ + ... + \cos 180^\circ \) là
– 1;
1;
0;
\(\sqrt 3 \).
Cho \(\Delta ABC\) có \(AB = 9;\,BC = 8;\,\widehat B = 60^\circ \). Tính độ dài \(AC\).
\(\sqrt {73} \);
\(\sqrt {217} \);
8;
\(\sqrt {113} \).
Vectơ có điểm đầu là \(A\), điểm cuối là \(E\) được kí hiệu là
\(AE\);
\(\left| {\overrightarrow {AE} } \right|\);
\(\overrightarrow {EA} \);
\(\overrightarrow {AE} \).
Mệnh đề nào sau đây đúng?
Hai vectơ cùng phương thì chúng cùng hướng;
Hai vectơ cùng phương thì giá của chúng song song hoặc trùng nhau;
Hai vectơ có giá vuông góc thì cùng phương;
Hai vectơ cùng hướng với một vectơ thứ ba thì cùng hướng.
Cho hình bình hành \(ABCD\). Vectơ tổng \(\overrightarrow {CB} + \overrightarrow {CD} \) bằng
\(\overrightarrow {CA} \);
\(\overrightarrow {BD} \);
\(\overrightarrow {AC} \);
\(\overrightarrow {DB} \).
Gọi \(O\) là tâm hình vuông \(ABCD\). Tính \(\overrightarrow {OB} - \overrightarrow {OC} \).
\(\overrightarrow {BC} \);
\(\overrightarrow {DA} \);
\(\overrightarrow {OD} - \overrightarrow {OA} \);
\(\overrightarrow {AB} \).
Cho bốn điểm \(A,\,B,\,C,\,D\) phân biệt. Khi đó vectơ \(\overrightarrow u = \overrightarrow {AD} - \overrightarrow {CD} + \overrightarrow {CB} - \overrightarrow {DB} \) bằng
\(\overrightarrow u = \overrightarrow 0 \);
\(\overrightarrow u = \overrightarrow {AD} \);
\(\overrightarrow u = \overrightarrow {CD} \);
\(\overrightarrow u = \overrightarrow {AC} \).
Khẳng định nào sau đây sai?
\(1\, \cdot \overrightarrow a = \overrightarrow a \);
\(k\overrightarrow a \) và \(\overrightarrow a \) cùng hướng khi \(k > 0\);
\(k\overrightarrow a \) và \(\overrightarrow a \) cùng hướng khi \(k < 0\);
Hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \ne \overrightarrow 0 \) cùng phương khi có một số \(k\) để \(\overrightarrow a = k\overrightarrow b \).
Tìm giá trị của \(k\) sao cho \(\overrightarrow a = k\overrightarrow b \), biết rằng \(\overrightarrow a ,\,\overrightarrow b \) ngược hướng và \(\left| {\overrightarrow a } \right| = 3,\,\,\left| {\overrightarrow b } \right| = 9\).
\(k = 3\);
\(k = - 3\);
\(k = \frac{1}{3}\);
\(k = - \frac{1}{3}\).
Cho hình bình hành \(ABCD\) có \(E,\,N\) lần lượt là trung điểm của \(BC,\,AE\). Tìm các số \(p\) và \(q\) sao cho \(\overrightarrow {DN} = p\overrightarrow {AB} + q\overrightarrow {AC} \).
\(p = \frac{5}{4};\,q = \frac{3}{4}\);
\(p = - \frac{3}{4};\,q = \frac{2}{3}\);
\(p = - \frac{4}{3};\,q = - \frac{2}{3}\);
\(p = \frac{5}{4};\,q = - \frac{3}{4}\).
Cho hai tam giác \(ABC\) và \(A'B'C'\) có trọng tâm lần lượt là \(G\) và \(G'\). Đẳng thức nào sau đây đúng?
\(\overrightarrow {A'A} + \overrightarrow {B'B} + \overrightarrow {C'C} = 3\overrightarrow {GG'} \);
\(\overrightarrow {AB'} + \overrightarrow {BC'} + \overrightarrow {CA'} = 3\overrightarrow {GG'} \);
\(\overrightarrow {AC'} + \overrightarrow {BA'} + \overrightarrow {CB'} = 3\overrightarrow {GG'} \);
\(\overrightarrow {AA'} + \overrightarrow {BB'} + \overrightarrow {CC'} = 3\overrightarrow {GG'} \).
Trong mặt phẳng tọa độ \[Oxy\], cho vectơ \(\overrightarrow v = 5\overrightarrow i - 2\overrightarrow j \). Tọa độ của vectơ \(\overrightarrow v \)là
\(\overrightarrow v = \left( {5;\, - 2} \right)\);
\(\overrightarrow v = \left( {5;\,2} \right)\);
\(\overrightarrow v = \left( { - 5;\, - 2} \right)\);
\(\overrightarrow v = \left( { - 5;\,2} \right)\).
Trong mặt phẳng tọa độ \(Oxy\), cho hai điểm \(M\left( {1;\,\,1} \right)\) và \(N\left( {4;\, - 1} \right)\). Tính độ dài vectơ \(\overrightarrow {MN} \).
\(\left| {\overrightarrow {MN} } \right| = \sqrt {13} \);
\(\left| {\overrightarrow {MN} } \right| = 5\);
\(\left| {\overrightarrow {MN} } \right| = \sqrt {29} \);
\(\left| {\overrightarrow {MN} } \right| = 3\).
Cho tam giác \(ABC\) có \(A\left( {4;\,9} \right)\), \(B\left( {3;\,7} \right)\), \(C\left( {x - 1;\,y} \right)\). Để \(G\left( {x;\,y + 6} \right)\) là trọng tâm của tam giác \(ABC\) thì giá trị \(x\) và \(y\) là
\(x = 3,\,y = 1\);
\(x = - 3,\,y = - 1\);
\(x = - 3,\,y = 1\);
\(x = 3,\,y = - 1\).
Cho \(\overrightarrow a \) và \(\overrightarrow b \) là hai vectơ cùng hướng và đều khác vectơ \(\overrightarrow 0 \). Mệnh đề nào sau đây đúng?
\(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right|\);
\(\overrightarrow a \cdot \overrightarrow b = 0\);
\(\overrightarrow a \cdot \overrightarrow b = - 1\);
\(\overrightarrow a \cdot \overrightarrow b = - \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right|\).
Cặp vectơ nào sau đây vuông góc?
\(\overrightarrow a = \left( {2;\, - 1} \right)\) và \(\overrightarrow b = \left( { - 3;\,4} \right)\);
\(\overrightarrow a = \left( {2;\,5} \right)\) và \(\overrightarrow b = \left( {5;\,2} \right)\);
\(\overrightarrow a = \left( {2;\,\,3} \right)\) và \(\overrightarrow b = \left( { - 6;\,\,4} \right)\);
\(\overrightarrow a = \left( {6;\, - 3} \right)\) và \(\overrightarrow b = \left( {3;\, - 6} \right)\).
Cho hình vuông \(ABCD\) với độ dài cạnh bằng \(a\). Tích vô hướng \(\overrightarrow {AB} \cdot \overrightarrow {AC} \) bằng
\({a^2}\sqrt 2 \);
\(\frac{{{a^2}}}{{\sqrt 2 }}\);
\({a^2}\);
\(\frac{{{a^2}}}{2}\).
Cho tam giác \(ABC\) có \(AB = 1\), \(BC = 2\) và \(\widehat {ABC} = 60^\circ \). Tích vô hướng \(\overrightarrow {BC} \cdot \overrightarrow {CA} \) bằng
\(\sqrt 3 \);
\( - \sqrt 3 \);
\(3\);
\( - 3\).
Số quy tròn của số gần đúng \(a\) trong trường hợp \(\overline a = 278,82 \pm 0,08\) là
278,82;
278,8;
278,2;
280.
Cho giá trị gần đúng của \(\frac{{23}}{7}\) là 3,28. Sai số tuyệt đối của số 3,28 là
0,004;
\(\frac{{0,04}}{7}\);
0,06;
Đáp án khác.
Số đặc trưng nào sau đây đo xu thế trung tâm của mẫu số liệu?
Phương sai;
Độ lệch chuẩn;
Khoảng tứ phân vị;
Số trung vị.
Số áo sơ mi bán được trong một tháng ở một cửa hàng quần áo được thống kê như sau:
Cỡ áo | 36 | 37 | 38 | 39 | 40 | 41 | 42 |
Số áo bán được | 18 | 5 | 10 | 25 | 10 | 8 | 5 |
Giá trị mốt của mẫu số liệu trên là
39;
25;
42;
36.
Điểm kiểm tra môn Toán cuối học kì 1 của một nhóm gồm 9 học sinh lớp 10 lần lượt là 5; 6; 8; 9; 8; 7; 6; 9; 7. Điểm trung bình của cả nhóm gần nhất với số nào dưới đây?
7;
7,1;
7,3;
7,5.
Trung vị của mẫu số liệu trong Câu 30 là
6;
7;
8;
9.
Để đánh giá mức độ phân tán của mẫu số liệu thống kê, ta dùng đại lượng nào sau đây?
Số trung bình;
Số trung vị;
Mốt;
Phương sai.
Cho phương sai của mẫu số liệu bằng 9. Độ lệch chuẩn của mẫu số liệu đó là
9;
3;
81;
18.
Cho mẫu số liệu sau: 165; 162; 187; 164; 170; 183; 175; 176; 175. Khoảng biến thiên của mẫu số liệu trên là
22;
23;
24;
25.
Khoảng tứ phân vị của mẫu số liệu ở Câu 34 là
15;
4,5;
175;
10,5.
II. Tự luận (3 điểm)
(1 điểm) Các góc nhìn đến đỉnh núi so với mực nước biển được đo từ hai đèn tín hiệu \(A\) và \(B\) trên biển được thể hiện trên hình vẽ. Nếu các đèn tín hiệu cách nhau 1 536 m thì ngọn núi cao bao nhiêu? (Làm tròn kết quả đến hàng phần trăm)
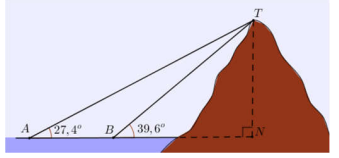
(1 điểm) Cho tam giác \(ABC\) có \(A\left( {1;\,\,1} \right),\,B\left( {2;\,4} \right),\,C\left( {10;\, - 2} \right)\).
a) Chứng minh tam giác \(ABC\) vuông cân tại \(A\).
b) Tính tích vô hướng \(\overrightarrow {BA} \cdot \overrightarrow {BC} \) và tính \(\cos B,\,\,\cos C\).
(1 điểm) Người ta tiến hành phỏng vấn một số người về chất lượng của một sản phẩm mới. Người điều tra yêu cầu cho điểm sản phẩm (thang điểm 100) được kết quả như sau:
10 15 20 60 80 90 76 87 88 90
Tìm các giá trị bất thường (nếu có) của mẫu số liệu trên.








