Bộ 10 đề thi Giữa kì 1 Toán 10 Kết nối tri thức có đáp án - Đề 10
28 câu hỏi
Cho mệnh đề chứa biến chia hết cho 2. Với giá trị nào của \(a\) ta được mệnh đề đúng?
\(a = - 2\);
\(a = 4\);
\(a = - 1\);
\(a = 0\).
Trong các câu sau, câu không phải mệnh đề là
\(x > 3\);
Tam giác cân có một góc bằng \(45^\circ \) là tam giác vuông cân;
Trong một tam giác tổng hai cạnh lớn hơn cạnh còn lại;
\(135\) là một số nguyên tố.
Cho mệnh đề . Mệnh đề phủ định của mệnh đề \(A\) là
;
;
;
.
Phát biểu nào sau đây là mệnh đề?
Máy bay đi thật nhanh;
Bí mật làm nên vẻ đẹp của người phụ nữ;
Đề thi cuối kì I môn Toán thật là khó;
Chất diệp lục làm nên màu xanh của lá cây.
Cho tập hợp \(K\) được biểu diễn trên trục số như sau:

Phần bù của tập hợp \(K\) trong \(\mathbb{R}\) là:
\(\left( { - \infty ; - 2} \right]\);
\(\left( {10;\,\, + \infty } \right)\);
\(\left( { - \infty ; - 2} \right] \cup \left( {10;\,\, + \infty } \right)\);
\(\left( { - \infty ; - 2} \right) \cup \left[ {10;\,\, + \infty } \right)\).
Trong các tập hợp sau, tập hợp nào là tập khác rỗng?
\(M = \left\{ {x \in \mathbb{N}|{x^2} + 16 = 0} \right\}\);
\(N = \left\{ {x \in \mathbb{R}|{x^2} + 2x + 5 = 0} \right\}\);
\(P = \left\{ {x \in \mathbb{Z}|{x^2} - 5 = 0} \right\}\);
\(Q = \left\{ {x \in \mathbb{Q}|{x^2} + 3x - 4 = 0} \right\}\).
Cho tập hợp \(M = \left\{ { - 3;\,\,4;\,\,a;\,\,d} \right\}\). Có bao nhiêu tập hợp con của \(M\) có \(2\) phần tử?
\(6\);
\(4\);
\(16\);
\(5\).
Mệnh đề nào dưới đây là đúng?
\(\left( {0;\,\,3} \right] \subset \left( { - 1;\,3} \right)\);
\(\left( { - 1;2} \right) \subset \mathbb{Q}\);
\(\left( { - 1;\,\,4} \right) \cup \left[ {5;\,\,6} \right] \subset \mathbb{Z}\);
\(\left\{ {\frac{1}{2}} \right\} \subset \mathbb{Q}\).
Cho ba tập hợp \(A,\,\,B,C\) như hình bên dưới:
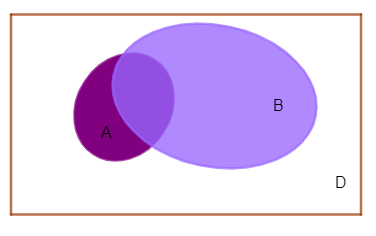
Phần không tô màu trong hình tương ứng với tập hợp nào sau đây?
\(D\);
\({C_D}\left( {A \cap B} \right)\);
\({C_D}\left( {A \cup B} \right)\);
\(A \cup B\).
Lớp 10A2 có \(21\) học sinh đạt học lực giỏi và \(24\) học sinh đạt hạnh kiểm tốt. Trong đó có \(15\) học sinh vừa đạt học lực giỏi và đạt hạnh kiểm tốt, \(11\) học sinh không đạt học lực giỏi và đạt hạnh kiểm tốt. Hỏi lớp 10A2 có bao nhiêu học sinh?
\(41\);
\(19\);
\(49\);
\(45\).
Bất phương trình nào dưới đây là bất phương trình bậc nhất hai ẩn?
\(\frac{4}{x} + \frac{2}{y} > - 1\);
\(x - 1 \le - 1 - 2y\);
\({x^2} - y > - \frac{1}{2}\);
\(9xy \ge 0\).
Miền không gạch chéo (không kể biên) là miền nghiệm của bất phương trình bậc nhất hai ẩn được biểu diễn bởi hình vẽ sau:
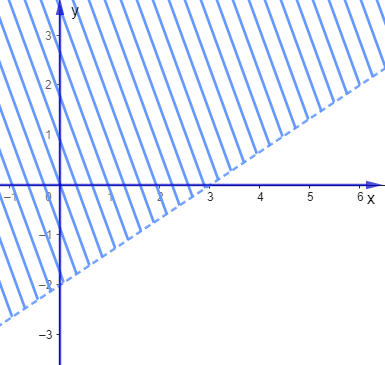
Điểm nào sau đây thuộc miền nghiệm của bất phương trình đã cho?
\(\left( {3;\,\,0} \right)\);
\(\left( {0;\,\, - 2} \right)\);
\((0;\,\,0)\);
\(\left( {5;0} \right)\).
Cho bất phương trình bậc nhất hai ẩn: \(\sqrt 3 x - 2y < \frac{{\sqrt 3 }}{9}\). Tìm điều kiện của \(m\) để cặp \(\left( {5 - m;\,\,2\sqrt 3 } \right)\) là nghiệm của bất phương trình đã cho.
\(m > \frac{8}{9}\);
\(m > \frac{{26}}{9}\);
\(m \le - \frac{{26}}{9}\);
\(m < - \frac{8}{9}\).
Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn
\(\left\{ \begin{array}{l}3{x^2} + y < 0\\x + 2y > 3\end{array} \right.\);
\(\left\{ \begin{array}{l}\frac{1}{x} - \frac{1}{y} < 0\\x + 2y \ge 0\end{array} \right.\);
\(\left\{ \begin{array}{l}\frac{x}{2} - y > 0\\x + \frac{y}{3} \le 10\end{array} \right.\);
\(\left\{ \begin{array}{l}x + y > 0\\{x^2} - y \le 0\end{array} \right.\).
Điểm \(O\left( {0;\,\,0} \right)\) thuộc miền nghiệm của hệ bất phương trình nào sau đây?
\(\left\{ \begin{array}{l}x + y < 0\\x + 2y > 3\end{array} \right.\);
\(\left\{ \begin{array}{l}x + 3y - 2 < 0\\2x + y \ge 0\end{array} \right.\);
\(\left\{ \begin{array}{l}x - y > - 9\\x + y + 2 \le 0\end{array} \right.\);
\(\left\{ \begin{array}{l}x + y > 0\\x - y - 1 \ge 0\end{array} \right.\).
Mỗi ngày bạn Thảo đều dành không quá 30 phút để đọc hai cuốn sách \(A\) và \(B\). Trung bình Thảo đọc được 3 trang sách \(A\) trong 2 phút và đọc được 2 trang sách \(B\) trong 1 phút. Gọi \(x\) và \(y\) lần lượt là số phút Thảo dùng để đọc sách \(A\) và sách \(B\)\[\left( {x\,,\,\,y \in \mathbb{N}} \right)\]. Tìm điều kiện cần và đủ của \(x\) và \(y\) để Thảo đọc được ít nhất 35 trang sách mỗi ngày.
\[\left\{ \begin{array}{l}3x + 4y \ge 70\\x + y \le 30\end{array} \right.\];
\[\left\{ \begin{array}{l}3x + 2y \ge 35\\x + y \le 30\end{array} \right.\];
\[3x + 4y \ge 70\];
\(3x + 2y \ge 35\).
Trong các đẳng thức sau đây đẳng thức nào là sai?
\({\rm{cos}}\left( { - {\rm{3}}0^\circ } \right) = - \frac{{\sqrt 3 }}{2}\);
\(\cot \left( { - 60^\circ } \right) = - \frac{1}{{\sqrt 3 }}\);
\(\sin \left( { - 120^\circ } \right) = - \frac{{\sqrt 3 }}{2}\);
\(\tan \left( { - 150^\circ } \right) = - \frac{{\sqrt 3 }}{3}\).
Giá trị của biểu thức \(M = \tan 150^\circ + \cot 30^\circ \) xấp xỉ
\(M = - \frac{{\sqrt 3 }}{3}\);
\(M = \frac{{2\sqrt 3 }}{3}\);
\(M = \sqrt 3 \);
\(M = \frac{{ - 4\sqrt 3 }}{3}\).
Cho góc \(\alpha \left( {90^\circ < \alpha < 180^\circ } \right)\) thỏa mãn \[{\rm{cos}}\alpha = \frac{{\sqrt 2 }}{2}\]. Khi đó \[\tan \alpha \] bằng
\(1\);
\( - 1\);
\( \pm 1\);
\( \pm \frac{1}{{\sqrt 2 }}\).
Cho tam giác \(ABC\). Tính \(P = \sin \frac{A}{2}.cos\left( {\frac{{B + C}}{2}} \right)\).
\(P = 1\);
\(P = 0\);
\(P = {\rm{co}}{{\rm{s}}^2}\frac{A}{2}\);
\(P = {\rm{si}}{{\rm{n}}^2}\frac{A}{2}\).
Cho \(\alpha \) thỏa mãn \(\tan \alpha = - 4\). Nhận xét nào sau đây đúng về giá trị của biểu thức \(P = \frac{{\frac{1}{2}\sin \alpha + \cos \alpha }}{{\cos \alpha - 3\sin \alpha }}\) ?
\(P > - \frac{1}{2}\);
\(P = \frac{1}{{13}}\);
\(P < - \frac{1}{4}\);
\(P = \frac{1}{{12}}\).
Giá trị lượng giác nào dưới đây bằng với \[{\rm{cos37}}^\circ \]?
\(\sin 143^\circ \);
\({\rm{cos}}143^\circ \);
\(\sin 53^\circ \);
\({\rm{cos5}}3^\circ \).
Trong tam giác \(ABC\), phát biểu nào sau đây đúng?
\[{\rm{cosA = }}\frac{{{b^2} + {c^2} - {a^2}}}{{ - 2bc}}\];
\({b^2} = {a^2} + {c^2} - 2ac.{\rm{cos}}B\);
\(\frac{c}{{\sin C}} = R\);
\(a.\sin A = b.\sin B\).
Gọi \(K\) là chu vi tam giác \(ABC\) có \(a = 8\,\,cm,\,b = 5\,\,cm,\,\,\widehat C = 175^\circ \). Giá trị \(K\) của gần nhất với giá trị nào sau đây?
\(25\);
\(13\);
\(26\);
\(36\).
Cho tam giác \(ABC\) có \(R = \sqrt 2 ,\widehat {BAC} = 60^\circ \). Độ dài cạnh BC bằng
\(4\sqrt 2 \);
\(\frac{{\sqrt 2 }}{2}\);
\(\sqrt 2 \);
\(2\sqrt 2 \).
PHẦN II. TỰ LUẬN (3 điểm)
(1,0 điểm)
a) Cho hai tập hợp \(A = \left\{ {x \in \mathbb{Z}|\left( {2x - 1} \right)\left( {{x^2} - 4} \right) = 0} \right\}\) và \(B = \left\{ {x \in \mathbb{N}|\left| x \right| \le 3} \right\}\). Tìm tập hợp \(A \cup B\).
b) Cho hai tập hợp \(M = \left( {0;3} \right)\) và \(N = \left[ {m;m + 1} \right)\), với \(m \in \mathbb{R}\). Tìm \(m\) để \(M \cap N = N\).
Giả sử \(CD = h\) là chiều cao của tháp trong đó \(C\) là chân tháp. Chọn hai điểm \(A,B\) trên mặt đất sao cho ba điểm \(A,\,B,\,C\) thẳng hàng. Ta đo được \(AB = 24\,m\), \(\widehat {CAD} = 63^\circ \), \(\widehat {CBD} = 48^\circ \) (tham khảo hình vẽ).
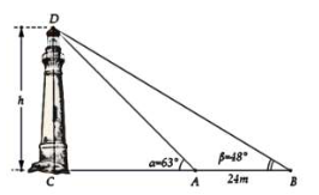
Tính gần đúng chiều cao \(h\) của khối chóp.
(1,0 điểm)
Một hộ nông dân định trồng củ đậu và dứa trên diện tích \(8\,\,ha\). Trên mỗi \(ha\), nếu trồng dứa thì cần \(20\) công và thu được \(5\) triệu đồng, nếu trồng củ đậu thì cần \(30\) công và thu được \(4\) triệu đồng. Hỏi cần trồng mỗi loại cây trên với diện tích là bao nhiêu \(ha\) để thu được nhiều tiền nhất, biết rằng tổng số công không quá \(180\)?








