Bộ 10 đề thi cuối kì 1 Toán 10 Kết nối tri thức có đáp án - Đề 5
38 câu hỏi
I. Trắc nghiệm (7 điểm)
Trong các câu sau, có bao nhiêu câu là không phải là mệnh đề?
a) Tháng 2 năm 2022 có 28 ngày.
b) Hãy trả lời câu hỏi này!
c) \(2x > 3\);
d) Bạn có thích chiếc vòng này không?
1;
2;
3;
4.
Cho tập hợp \(A = \left\{ {x \in \mathbb{N}|{x^2} - 4 = 0} \right\}\). Tập hợp con của \(A\) là
\(\left\{ {0;\,\,2} \right\}\);
\(\left\{ 2 \right\}\);
\(\left\{ { - 2} \right\}\);
\(\left\{ { - 2;2} \right\}\).
Cho hai tập hợp \(A = \left\{ {x \in \mathbb{Z}|{x^2} - 4 = 0} \right\}\)và \(B = \left\{ {0 \le x < 10|x \vdots 2} \right\}\). Ta có\(A \cap B = ?\)
\(\left\{ {0;2} \right\}\);
\(\emptyset \);
\(\left\{ 2 \right\}\);
\(\left\{ { - 2;2} \right\}\).
Miền nghiệm của bất phương trình \(x + y \le 2\) là phần tô đậm của hình vẽ nào trong các hình vẽ sau?
A. 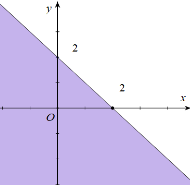 ;
;
B. 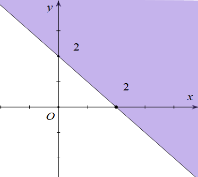 ;
;
C. 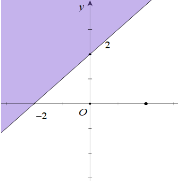 ;
;
D. 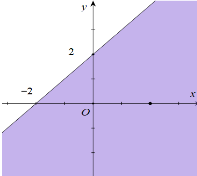 .
.
Hệ phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn?
\(\left\{ \begin{array}{l}x - {y^2} \ge 4\\{x^2} - y < - 2\end{array} \right.\);
\(\left\{ \begin{array}{l}x - y + z < - 1\\2x - y - z > 4\end{array} \right.\);
\(\left\{ \begin{array}{l}3x - 4y > 4\\2x - y \le - 2\end{array} \right.\);
\(\left\{ \begin{array}{l}{x^2} = 4\\x - y > - 5\end{array} \right.\).
Cho góc \(\alpha \) với \(0^\circ \le \alpha \le 180^\circ \). Khẳng định nào sau đây là đúng ?
\(\tan (180^\circ - \alpha ) = \tan \alpha \);
\(\cot (180^\circ - \alpha ) = \cot \alpha \);
\(\cos (180^\circ - \alpha ) = \cos \alpha \);
\(\sin (180^\circ - \alpha ) = \sin \alpha \).
Cho góc \(\alpha = 60^\circ \). Giá trị \(\tan \alpha \) bằng
\(\sqrt 3 \);
\(\frac{{\sqrt 3 }}{3}\);
1;
2.
Cho góc \(\alpha \ne 90^\circ \) với \(0^\circ \le \alpha \le 180^\circ \), biết \(\tan \alpha = \frac{{\sqrt 6 }}{2}\). Giá trị \(\tan (180^\circ - \alpha )\) bằng
\(\frac{{\sqrt 6 }}{2}\);
\( - \frac{{\sqrt 6 }}{2}\);
\(\frac{2}{{\sqrt 6 }}\);
\( - \frac{2}{{\sqrt 6 }}\).
Tam giác \(ABC\) có \(AB = 3\,\,{\rm{cm}}\), \(BC = 4\,\,{\rm{cm}}\), \(\widehat {ABC} = 60^\circ \). Độ dài cạnh \(AC\) bằng
\(AC = \sqrt {13} \)cm;
\(AC = 13\) cm;
\(AC = 5\) cm;
\(AC = \sqrt {11} \) cm.
Khẳng định nào sau đây là đúng ?
Hai vectơ được gọi là cùng phương chỉ khi giá của 2 vectơ đó song song với nhau;
Hai vectơ được gọi là cùng phương khi giá của 2 vectơ đó vuông góc với nhau;
Hai vectơ được gọi là cùng phương khi giá của 2 vectơ đó song song hoặc trùng với nhau;
Hai vectơ được gọi là cùng phương khi giá của 2 vectơ đó cắt nhau.
Cho hình vẽ, cặp vectơ nào dưới đây cùng phương?
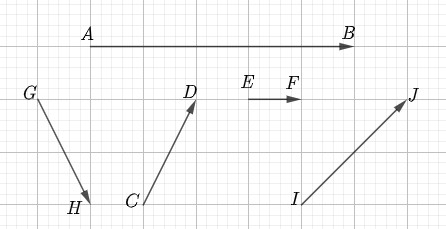
\(\overrightarrow {AB} \) và \(\overrightarrow {GH} \);
\(\overrightarrow {AB} \) và \(\overrightarrow {IJ} \);
\(\overrightarrow {EF} \) và \(\overrightarrow {AB} \);
\(\overrightarrow {GH} \) và \(\overrightarrow {CD} \).
Cho ba điểm \(A\), \(B\), \(C\) phân biệt. Khẳng định nào sau đây là đúng?
\(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \);
\(\overrightarrow {AB} - \overrightarrow {BC} = \overrightarrow {AC} \);
\(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {CA} \);
\(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow 0 \).
Cho 4 điểm \(A\), \(B\), \(C\), \(D\) là 4 đỉnh của hình bình hành \(ABCD\). Khẳng định nào sau đây là sai ?
\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \);
\(\overrightarrow {CB} + \overrightarrow {CD} = \overrightarrow {CA} \);
\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {BD} \);
\(\overrightarrow {DA} + \overrightarrow {DC} = \overrightarrow {DB} \).
Cho tam giác \(ABC\) vuông tại \(B\), tính độ dài vectơ \(\overrightarrow u = \overrightarrow {BC} - \overrightarrow {BA} \). Biết \(AB = 3\), \(BC = 5\).
\(\left| {\overrightarrow u } \right| = 8\);
\(\left| {\overrightarrow u } \right| = 2\);
\(\left| {\overrightarrow u } \right| = 4\);
\(\left| {\overrightarrow u } \right| = \sqrt {34} \).
Cho tam giác \(ABC\) có trọng tâm \(G\). Với điểm \(M\) bất kì, khẳng định nào sau đây là đúng ?
\(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = 3\overrightarrow {AB} \);
\(3\overrightarrow {MA} + 2\overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \);
\(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow {3MG} \);
\(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {GA} \).
Chọn phát biểu sai trong các phát biểu sau ?
Ba điểm \(A\), \(B\), \(C\) phân biệt thẳng hàng khi và chỉ khi \(\overrightarrow {AB} = k\overrightarrow {BC} \), \(k \ne 0\);
Ba điểm \(A\), \(B\), \(C\) phân biệt thẳng hàng khi và chỉ khi \(\overrightarrow {AC} = k\overrightarrow {BC} \), \(k \ne 0\);
Ba điểm \(A\), \(B\), \(C\) phân biệt thẳng hàng khi và chỉ khi \(\overrightarrow {AB} = k\overrightarrow {AC} \), \(k \ne 0\);
Ba điểm \(A\), \(B\), \(C\) phân biệt thẳng hàng khi và chỉ khi \(\overrightarrow {AB} = k\overrightarrow {AC} \).
Trên đường thẳng \(MN\) lấy điểm \(P\) ở giữa hai điểm như hình vẽ. Đẳng thức nào sau đây là đúng ?
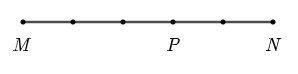
\(\overrightarrow {MP} = 3\overrightarrow {NP} \);
\(\overrightarrow {MP} = \frac{3}{2}\overrightarrow {PN} \);
\(\overrightarrow {MP} = \frac{3}{2}\overrightarrow {NP} \);
\(\overrightarrow {MP} = 5\overrightarrow {PN} \).
Cho tam giác \(ABC\) có trung tuyến \(BM\) và trọng tâm \(G\). Khi đó \(\overrightarrow {BG} = \) ?
\(\overrightarrow {BA} + \overrightarrow {BC} \);
\(\frac{1}{2}\left( {\overrightarrow {BA} + \overrightarrow {BC} } \right)\);
\(\frac{1}{3}\overrightarrow {BA} + \overrightarrow {BC} \);
\(\frac{1}{3}\left( {\overrightarrow {BA} + \overrightarrow {BC} } \right)\).
Trong mặt phẳng tọa độ \(Oxy\), cho vectơ \(\overrightarrow b = 3\overrightarrow i - 5\overrightarrow j \). Tọa độ của vectơ \(\overrightarrow b \) là
\(\left( {3;5} \right)\);
\(\left( {3; - 5} \right)\);
\(\left( { - 3; - 5} \right)\);
\(\left( { - 3;5} \right)\).
Trong mặt phẳng tọa độ \(Oxy\), cho điểm \[A\left( {3;\,4} \right)\]và \[B\left( {3;\,7} \right)\]. Tọa độ vectơ \(\overrightarrow {AB} \) là
\(\left( {0;\,\,3} \right)\);
\(\left( {6;\,\,11} \right)\);
\(\left( {4;\,\,3} \right)\);
\(\left( {6;\,\,3} \right)\).
Cho các vectơ \(\overrightarrow u = \left( {3;6} \right)\), \(\overrightarrow v = \left( {1;2} \right)\). Khẳng định nào sau đây là đúng ?
\(\overrightarrow u \) và \(\overrightarrow v \) cùng phương cùng hướng;
\(\overrightarrow u \) và \(\overrightarrow v \) cùng phương ngược hướng;
\(\overrightarrow u \) và \(\overrightarrow v \) bằng nhau;
\(\overrightarrow u = 2\overrightarrow v \).
Chọn khẳng định đúng nhất.
Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) khác vectơ \(\overrightarrow 0 \). Tích vô hướng của \(\overrightarrow a \) và \(\overrightarrow b \) là một số, được ký hiệu là \(\overrightarrow a \cdot \overrightarrow b \) và xác định bởi công thức: \(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot cos\left( {\overrightarrow a ,\overrightarrow b } \right)\);
Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \). Tích vô hướng của \(\overrightarrow a \) và \(\overrightarrow b \) là một số, được ký hiệu là \(\overrightarrow a \cdot \overrightarrow b \) và xác định bởi công thức: \(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot cos\left( {\overrightarrow a ,\overrightarrow b } \right)\);
Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) khác vectơ \(\overrightarrow 0 \). Tích vô hướng của \(\overrightarrow a \) và \(\overrightarrow b \) là một số, được ký hiệu là \(\overrightarrow a \cdot \overrightarrow b \) và xác định bởi công thức: \(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot \sin \left( {\overrightarrow a ,\overrightarrow b } \right)\);
Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) khác vectơ \(\overrightarrow 0 \). Tích vô hướng của \(\overrightarrow a \) và \(\overrightarrow b \) là một số, được ký hiệu là \(\overrightarrow a \cdot \overrightarrow b \) và xác định bởi công thức: \(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right|\).
Cho các vectơ \(\overrightarrow a \) và \(\overrightarrow b \) khác vectơ \(\overrightarrow 0 \). Nếu \(\overrightarrow a \) và \(\overrightarrow b \) vuông góc thì \(\overrightarrow a .\overrightarrow b \) bằng
0;
1;
– 1;
2.
Cho tam giác \(ABC\) đều. Số đo góc giữa hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) bằng
\(60^\circ \);
\(90^\circ \);
\(120^\circ \);
\(140^\circ \).
Cho các vectơ \(\overrightarrow a = \left( {3;4} \right)\) và \(\overrightarrow b = \left( {0;2} \right)\). Tích vô hướng \(\overrightarrow a \cdot \overrightarrow b \) bằng
9;
– 8;
8;
0.
Giả sử biết số đúng là 8 217,3. Sai số tuyệt đối khi quy tròn số này đến hàng chục là
7,3;
2,3;
0,3;
2,7.
Chiều dài của một cái bàn đo được là \(l\) = 1,2564 m ± 0,001 m. Số quy tròn của số \(l\) = 1,2564 m là:
1,26 m;
1,3 m;
1,25 m;
1,2 m.
Cho mẫu số liệu sau:
1 2 3 3 5 6 8 9 9.
Trung vị của mẫu số liệu trên là
5;
2;
3;
6.
Cho bảng số liệu ghi lại điểm của 40 học sinh trong bài kiểm tra 1 tiết môn toán như sau:
Điểm | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Cộng |
Số HS | 2 | 3 | 7 | 18 | 3 | 2 | 4 | 1 | 40 |
Điểm trung bình của 40 học sinh trên gần nhất với giá trị nào sau đây?
5;
6;
7;
8.
Cho mẫu số liệu:
3 5 5 2 9 10 9 8 5.
Mốt của mẫu số liệu trên là
3;
9;
5;
10.
Dân số Việt Nam (triệu người) qua các năm được thể hiện qua bảng sau:
Năm | Số dân |
1901 | 13,0 |
1921 | 15,5 |
1936 | 18,8 |
1956 | 27,5 |
1960 | 30,2 |
Tứ phân vị \({Q_2}\), \({Q_1}\), \({Q_3}\) của bảng số liệu này lần lượt là
18,8; 14,25; 28,85;
18; 14,25; 28,85;
18,8; 14,5; 28,5;
18,8; 13,0; 30,2.
Cho hai mẫu số liệu. Mẫu thứ nhất là: \(\left\{ {2;3;4;2;1;4;5} \right\}\). Mẫu thứ hai là: \(\left\{ {2;0;1;2;1;2;3} \right\}\). So sánh độ phân tán của hai mẫu số liệu dựa vào khoảng biến thiên, khẳng định nào sau đây là đúng ?
Mẫu số liệu thứ nhất có độ phân tán cao hơn;
Mẫu số liệu thứ hai có độ phân tán thấp hơn;
Hai mẫu số liệu có độ phân tán như nhau;
Không có khẳng định đúng.
Tiền lương hằng tháng (đơn vị: triệu đồng) của 7 nhân viên trong một công ty du lịch lần lượt là: 6,5; 8,4; 6,9; 7,2; 2,5; 6,7; 3,0.
Khoảng biến thiên của dãy số liệu thống kê trên bằng:
5,8;
6;
5,9;
5,7.
Cho mẫu số liệu:
7 8 9 8 8 7 7 9 9.
Khoảng tứ phân vị của mẫu số liệu trên là:
2;
3;
9;
8.
41 học sinh của một lớp kiểm tra chất lượng đầu năm (thang điểm 30) được kết quả như sau
Số lượng (Tần số) | 3 | 6 | 4 | 4 | 6 | 7 | 3 | 4 | 2 | 2 |
Điểm | 9 | 11 | 14 | 16 | 17 | 18 | 20 | 21 | 23 | 25 |
Phương sai của mẫu số liệu trên là
18,21;
18,22;
18,03;
18,04.
II. Tự luận (3 điểm)
(1 điểm) Hai chiếc tàu thủy cùng xuất phát từ một vị trí \(A\), đi thẳng theo hai hướng tạo với nhau một góc \(45^\circ \). Tàu \(B\) chạy với tốc độ 24 hải lí một giờ. Tàu \(C\) chạy với tốc độ 18 hải lí một giờ. Sau hai giờ, hai tàu cách nhau bao nhiêu hải lí ?
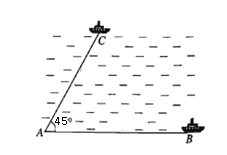
(1 điểm) Cho tam giác \(ABC\) với \(a = BC\), \(b = CA\), \(c = AB\) và một điểm \(M\) bất kỳ. Tìm giá trị nhỏ nhất của biểu thức \(T = \frac{{MA}}{a} + \frac{{MB}}{b} + \frac{{MC}}{c}\).
(1 điểm) Cho mẫu số liệu thống kê:
6 7 8 14 23 34 65 120.
Tìm các số liệu bất thường của mẫu số liệu trên.








