Bộ 10 đề thi cuối kì 1 Toán 10 Kết nối tri thức có đáp án - Đề 7
24 câu hỏi
I. Trắc nghiệm (6 điểm)
Mệnh đề đảo của mệnh đề “Nếu hình thang \(ABCD\) có \(AC = BD\) thì hình thang \(ABCD\) cân” là mệnh đề
“Nếu hình thang \(ABCD\) có \(AC = BD\) thì hình thang \(ABCD\) vuông”;
“Nếu hình thang \(ABCD\) cân thì hình thang \(ABCD\) có \(AC \ne BD\)”;
“Nếu hình thang \(ABCD\) cân thì hình thang \(ABCD\) có \(AC = BD\)”;
“Nếu hình thang \(ABCD\) cân thì hình thang \(ABCD\) có \(AC \bot BD\)”.
Cho tập hợp \(E = \left\{ {x \in \mathbb{N}|x = 10 - {n^2},n \in \mathbb{N}} \right\}\). Số phần tử của tập hợp \(E\) là
3;
4;
5;
vô số.
Cho hai tập hợp: \(A = \left[ { - 4;\,\,1} \right),B = \left[ { - 2;\,\,3} \right]\). Khi đó \(A \cap B\) là tập hợp nào sau đây?
\(\left( { - 4;\,3} \right)\);
\(\left[ { - 4;\,\,3} \right]\);
\(\left[ { - 2;\,\,1} \right)\);
\(\left( { - 2;\,\,1} \right)\).
Nửa mặt phẳng không bị gạch (kể cả đường thẳng \(d\)) dưới đây là miền nghiệm của bất phương trình nào trong các bất phương trình sau?
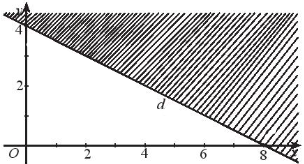
\(2x + y \le 8\);
\(2x + y > 8\);
\(2x + y < 8\);
\(2x + y \ge 8\).
Cho hệ bất phương trình \(\left\{ \begin{array}{l}2x - 3y \le 2\\ - x + y \ge - 1\end{array} \right.\). Cặp số nào sau đây không là nghiệm của hệ bất phương trình trên?
\(\left( {2;\,\,1} \right)\);
\(\left( { - 5;\,\, - 3} \right)\);
\(\left( {1;\,\, - 2} \right)\);
\(\left( { - 2;\,\,3} \right)\).
Trong các khẳng định sau, khẳng định nào sai?
\(\sin 45^\circ = \cos 45^\circ \);
\(\cos 45^\circ = \sin 135^\circ \);
\(\cos 30^\circ = - \cos 150^\circ \);
\(\sin 30^\circ = \cos 150^\circ \).
Cho tam giác \(ABC\) có \(AB = 7,\,AC = 9,\,BC = 4\). Giá trị \(\cos C\) bằng
\(\frac{2}{3}\);
\(\frac{1}{3}\);
\( - \frac{2}{3}\);
\(\frac{1}{2}\).
Vectơ có điểm cuối là \(M\), điểm đầu là \(N\) được kí hiệu là
\(\overrightarrow {MN} \);
\(\overrightarrow {NM} \);
\(\left| {\overrightarrow {MN} } \right|\);
\(NM\).
Cho ba điểm phân biệt \(A,\,\,B,\,\,C\). Khẳng định nào sau đây là đúng?
\[\overrightarrow {CA} - \overrightarrow {BA} = \overrightarrow {BC} \];
\[\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {BC} \];
\[\overrightarrow {AB} + \overrightarrow {CA} = \overrightarrow {CB} \];
\[\overrightarrow {AB} - \overrightarrow {BC} = \overrightarrow {CA} \].
Cho hình bình hành \(ABCD\) và điểm \(M\), biết \(\left| {\overrightarrow {BM} - \overrightarrow {BA} } \right| = \left| {\overrightarrow {AB} + \overrightarrow {AD} } \right|\). Điểm \(M\) là
điểm thuộc đường tròn tâm \(A\) bán kính \(AC\);
điểm thuộc đường tròn tâm \(A\) bán kính \(BD\);
điểm thuộc đường tròn tâm \(B\) bán kính \(AC\);
điểm thuộc đường tròn tâm \(B\) bán kính \(BD\).
Cho tam giác \[ABC\] có \[G\] trọng tâm và \(I\) là trung điểm của đoạn thẳng \(BC\). Khẳng định nào sau đây là đúng?
\[\overrightarrow {GA} = 2\overrightarrow {GI} \];
\[\overrightarrow {IG} = - \frac{1}{3}\overrightarrow {IA} \];
\[\overrightarrow {GB} + \overrightarrow {GC} = 2\overrightarrow {GI} \];
\[\overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {GA} \].
Cho tam giác \(ABC\). Gọi \(I\) là điểm thỏa mãn điều kiện \(\overrightarrow {IA} + 2\overrightarrow {IB} + 3\overrightarrow {IC} = \overrightarrow 0 \). Biểu thị vectơ \(\overrightarrow {AI} \) theo hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) là
\(\overrightarrow {AI} = \frac{1}{3}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AC} \);
\(\overrightarrow {AI} = - \frac{1}{3}\overrightarrow {AB} - \frac{1}{2}\overrightarrow {AC} \);
\(\overrightarrow {AI} = \frac{1}{3}\overrightarrow {AB} - \frac{1}{2}\overrightarrow {AC} \);
\(\overrightarrow {AI} = \frac{1}{3}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AC} \).
Trong mặt phẳng tọa độ \(Oxy\), cho hai điểm \(A\left( {1;\,\, - 2} \right)\) và \(B\left( {3;\, - 6} \right)\). Tọa độ vectơ \(\overrightarrow {AB} \) là
\(\overrightarrow {AB} = \left( {1;\,\, - 2} \right)\);
\[\overrightarrow {AB} = \left( {2;\,\, - 4} \right)\];
\(\overrightarrow {AB} = \left( {4;\,\, - 2} \right)\);
\(\overrightarrow {AB} = \left( { - 2;\,\,4} \right)\).
Cho tam giác \(ABC\) có \(A\left( {1;\,\,3} \right),\,\,B\left( {4;\, - 2} \right),\,C\left( {x;\,y - 1} \right)\). Xác định \(x,\,y\) để \(G\left( {2x;\,y + 2} \right)\) là trọng tâm của tam giác \(ABC\).
\(x = 1;\,\,y = - 3\);
\(x = - 1;\,y = - 3\);
\(x = - 3;\,y = 1\);
\(x = 1;\,y = - 2\).
Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng, biết \(\left| {\overrightarrow a } \right| = 5,\,\left| {\overrightarrow b } \right| = 3\). Giá trị \(\overrightarrow a \cdot \overrightarrow b \) bằng
– 15;
15;
\(\frac{3}{5}\);
\(\frac{5}{3}\).
Cho hai vectơ \(\overrightarrow a = \left( {m;m - 2} \right),\overrightarrow b = \left( {2; - 3} \right)\). Giá trị của \(m\) để hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) vuông góc là
\(m = 6\);
\(m = \pm 6\);
\(m = - 6\);
\(m = \frac{6}{5}\).
Cho số gần đúng \(a = 1,2568\) với độ chính xác \(d = 0,001\). Số quy tròn của số \(a\) là
1,257;
1,26;
1,256;
1,3.
Trung vị của mẫu số liệu: 4; 5; 5; 6; 7; 7; 8; 9; 9 là
6;
7;
8;
9.
Khảo sát điểm thi đầu vào môn Tiếng Anh (thang điểm 100) của một số sinh viên tại một trường đại học cho kết quả như sau:
90 50 80 80 50 56 85 30 50 40 35 80 95 60
Khoảng biến thiên của mẫu số liệu trên là
65;
60;
45;
40.
Một mẫu số liệu có độ lệch chuẩn bằng 2,5. Phương sai của mẫu số liệu đó là
2,5;
6,25;
1,58;
5.
II. Tự luận (4 điểm)
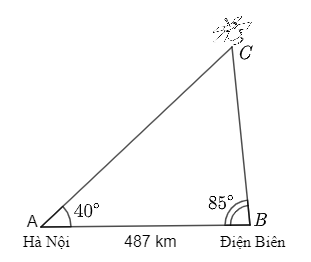
(1 điểm) Một vệ tinh quay quanh Trái Đất, đang bay phía trên hai trạm quan sát của hai thành phố Hà Nội và Điện Biên. Khi vệ tinh nằm giữa hai trạm này, góc nâng của nó được quan sát đồng thời là \(40^\circ \) tại Hà Nội và \(85^\circ \) tại Điện Biên. Hỏi vệ tinh đó cách trạm quan sát Điện Biên bao xa? Biết rằng, khoảng cách giữa hai trạm quan sát là 487 km.
(1 điểm) Trong mặt phẳng tọa độ \[Oxy\], cho tam giác \(ABC\) có ba đỉnh \(A\left( {1;\,2} \right),B\left( { - 1;\, - 1} \right),C\left( {2;\, - 1} \right)\). Tìm tọa độ trực tâm \(H\) của tam giác \(ABC\).
(1 điểm) Cho tam giác \(ABC\). Trên cạnh \(AB\) lấy điểm \(D\), trên cạnh \(BC\) lấy điểm \(E\) và điểm \(F\) sao cho \[\frac{{AD}}{{DB}} = \frac{3}{2}\], \[\frac{{BE}}{{EC}} = \frac{1}{3}\], \[\frac{{BF}}{{FC}} = \frac{4}{1}\]. Đường thẳng \(AE\) chia đoạn \(DF\) theo tỷ số \[\frac{{KD}}{{KF}} = k\]. Tính giá trị của \(k\).
(1 điểm) Kiểm tra khối lượng của 10 con gà ri trống trưởng thành được kết quả như sau (đơn vị: kilôgam)
1,8 2,4 1,9 2,2 0,5 1,9 1,8 1,9 2,0 2,1.
a) Hãy tìm số trung bình, khoảng biến thiên, khoảng tứ phân vị, độ lệch chuẩn của khối lượng gà ri trống trưởng thành.
b) Xác định các giá trị bất thường (nếu có) của mẫu số liệu trên.








