Bộ 10 đề thi cuối kì 1 Toán 10 Kết nối tri thức có đáp án - Đề 8
24 câu hỏi
I. Trắc nghiệm (6 điểm)
Trong các phát biểu sau, phát biểu nào là mệnh đề?
“Bất phương trình \(3x + 2 < 0\) có nghiệm”;
“Bất phương trình \(3x + 2 < 0\) có phải là bất phương trình bậc nhất hai ẩn không?”;
“Bất phương trình \(3x + 2 < 0\) là bất phương trình bậc nhất hai ẩn”;
“Bất phương trình \(3x + 2 < 0\) có vô số nghiệm”.
Cho tập hợp \(E = \left\{ {x \in \mathbb{N}|x = 7 - n,n \in \mathbb{N}} \right\}\). Viết tập hợp \(E\) dưới dạng liệt kê các phần tử ta được
\(E = \left\{ {1;\,\,2;\,\,3;\,\,4;\,\,5;\,\,6;\,\,7} \right\}\);
\(E = \left\{ {0;\,\,1;\,\,2;\,\,3;\,\,4;\,\,5;\,\,6;\,\,7} \right\}\);
\(E = \left\{ {0;\,\,1;\,\,2;\,\,3;\,\,4;\,\,5;\,\,6;\,\,7;\,\,8;\,\,9} \right\}\);
\(E = \left\{ {1;\,\,3;\,\,5;\,\,7} \right\}\).
Cho hai tập hợp: \(A = \left[ { - 4;\,\,1} \right),B = \left[ { - 2;\,\,3} \right]\). Khi đó \({C_\mathbb{R}}\left( {A \cup B} \right)\) là tập hợp nào sau đây?
\(\left( { - 4;\,3} \right)\);
\(\left[ { - 4;\,\,3} \right]\);
\(\left( { - \infty ; - 4} \right) \cup \left( {3; + \infty } \right)\);
\(\left( { - \infty ; - 4} \right] \cup \left( {3; + \infty } \right)\).
Bạn Hồng muốn pha hai loại nước cam. Để pha một lít nước cam loại 1 thì cần 900 ml nước cốt cam và còn nước cam loại 2 thì cần 850 ml nước cốt cam. Gọi \(x\) và \(y\) \(\left( {x \ge 0,y \ge 0} \right)\) lần lượt là số lít nước cam loại 1 và loại 2 pha chế được và biết rằng Hồng chỉ có 4,5 lít nước cốt cam. Bất phương trình mô tả số lít nước cam loại 1 và loại 2 mà bạn Hồng có thể pha chế được là
\(18x + 17y \le 90\);
\(18x + 17y > 90\);
\(18x + 17y \ge 90\);
\(18x + 17y < 9\).
Cho hệ bất phương trình \(\left\{ \begin{array}{l}x + 2y > 5\\2x - 5y < 9\end{array} \right.\). Cặp số nào sau đây không là nghiệm của hệ bất phương trình trên?
\(\left( {2;\,\,3} \right)\);
\(\left( {5;\,\,1} \right)\);
\(\left( { - 1;\,\,4} \right)\);
\(\left( { - 2;\,\, - 5} \right)\).
Tam giác \(ABC\) vuông tại \(B\) có \(\widehat A = 30^\circ \). Khi đó giá trị \(\sin C\) bằng
\(\frac{{\sqrt 3 }}{2}\);
\( - \frac{{\sqrt 3 }}{2}\);
\( - \frac{1}{2}\);
\(\frac{1}{2}\).
Cho tam giác \(ABC\) có \(AB = 9,\,\widehat B = 55^\circ ,\,\widehat C = 48^\circ \). Độ dài cạnh \(BC\) gần nhất với giá trị nào dưới đây?
11;
11,5;
11,8;
12.
Cho hình vuông \(ABCD\), vectơ \(\overrightarrow {AB} \) cùng phương với vectơ nào sau đây?
\(\overrightarrow {AC} \);
\(\overrightarrow {AD} \);
\(\overrightarrow {CD} \);
\(\overrightarrow {BC} \).
Cho ba điểm phân biệt \(A,\,\,B,\,\,C\). Khẳng định nào sau đây là đúng?
\[\overrightarrow {CA} - \overrightarrow {BA} = \overrightarrow {BC} \];
\[\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {BC} \];
\[\overrightarrow {AB} + \overrightarrow {CA} = \overrightarrow {CB} \];
\[\overrightarrow {AB} - \overrightarrow {BC} = \overrightarrow {CA} \].
Cho hình chữ nhật \(ABCD\), biết \(AB = 2a,\,\,BC = 3a\). Độ dài vectơ \(\overrightarrow {AB} + \overrightarrow {AD} \) là
\(a\sqrt {13} \);
\(a\sqrt 5 \);
\(5a\);
\(a\).
Cho hai vectơ \[\overrightarrow a ,\,\,\overrightarrow b \,\,\]không cùng phương và \[\overrightarrow {\,x\,} = - 2\overrightarrow {a\,} + \overrightarrow {\,b\,} \]. Vectơ cùng hướng với vectơ \[\overrightarrow {x\,} \]là
\[2\overrightarrow {a\,} - \overrightarrow {\,b\,} \];
\[ - \,\overrightarrow {a\,} + \frac{1}{2}\overrightarrow {b\,} \];
\[4\,\overrightarrow {a\,} + 2\overrightarrow {b\,} \];
\[ - \,\overrightarrow {a\,} + \overrightarrow b \].
Cho tam giác \[ABC\]có trọng tâm \(G\). Gọi \(M\) là trung điểm \(BC\). Phân tích vectơ \[\overrightarrow {AG} \]theo hai vectơ là hai cạnh của tam giác. Khẳng định nào sau đây đúng?
\(\overrightarrow {AG} = \frac{2}{3}\overrightarrow {AB} + \overrightarrow {AC} \);
\(\overrightarrow {AG} = \frac{1}{3}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AC} \);
\(\overrightarrow {AG} = \frac{2}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \);
\(\overrightarrow {AG} = \frac{1}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \).
Trong mặt phẳng tọa độ \(Oxy\), cho hai điểm \(A\left( {3;\,\, - 1} \right)\) và \(B\left( { - 2;\,5} \right)\). Độ dài đoạn thẳng \(AB\) bằng
\(\sqrt {61} \);
\[\sqrt {17} \];
\(\sqrt {41} \);
\(2\sqrt 5 \).
Trong mặt phẳng tọa độ \(Oxy\), cho các điểm \(M\left( {5;\,\,3} \right),\,\,N\left( {x;\,\,y} \right)\), \(P\left( {x - 4;y + 1} \right)\). Xác định \(x,\,y\) để \(P\) là trung điểm của \(MN\).
\(x = 1;\,\,y = 13\);
\(x = 13;\,y = 1\);
\(x = - 13;\,y = 1\);
\(x = - 1;\,y = 13\).
Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) ngược hướng, biết \(\left| {\overrightarrow a } \right| = 2,\,\left| {\overrightarrow b } \right| = 8\). Giá trị \(\overrightarrow a \cdot \overrightarrow b \) bằng
– 16;
16;
4;
\(\frac{1}{4}\).
Cho hình vuông \(ABCD\) tâm \(O\). Hỏi mệnh đề nào sau đây sai?
\(\overrightarrow {OA} \cdot \overrightarrow {OB} = 0\) ;
\(\overrightarrow {OA} \cdot \overrightarrow {OC} = \frac{1}{2}\overrightarrow {OA} \cdot \overrightarrow {AC} \);
\(\overrightarrow {AB} \cdot \overrightarrow {AC} = \overrightarrow {AB} \cdot \overrightarrow {CD} \);
\(\overrightarrow {AB} \cdot \overrightarrow {AC} = \overrightarrow {AC} \cdot \overrightarrow {AD} \).
Viết số quy tròn của số gần đúng \(a\) trong trường hợp \(\overline a = 20\,\,006\,\,851\, \pm 400\) ta được kết quả là
20 007 000;
20 006 900;
20 006 850;
20 006 851.
Trung vị của mẫu số liệu: 20; 25; 26; 35; 47; 56; 58; 59; 59 là
47;
42,8;
42,7;
56.
Điểm thi văn nghệ của 10 đội thi trong lễ hội văn nghệ chào mừng ngày Nhà giáo Việt Nam tại một trường THPT như sau:
80 90 95 100 90 80 75 90 80 85
Khoảng biến thiên của mẫu số liệu trên là
15;
20;
25;
30.
Phương sai của mẫu số liệu ở Câu 19 là
55,52;
52,25;
7,43;
55,25.
II. Tự luận (4 điểm)
(1 điểm) Một tháp viễn thông cao 48 m được dựng thẳng đứng trên một sườn dốc \(25^\circ \) so với phương ngang. Từ đỉnh tháp, người ta neo một sợi dây cáp xuống một điểm trên sườn dốc cách chân tháp 35 m như hình dưới. Tính chiều dài của sợi dây cáp đó.
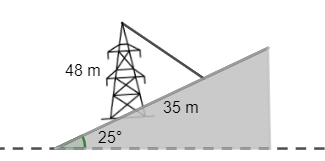
(1 điểm) Trong mặt phẳng tọa độ \(Oxy\), cho các điểm \[A\left( {1;\,\,3} \right),{\rm{ }}B\left( {0;\,\,2} \right),{\rm{ }}C\left( {4;\,\,5} \right).\] Xác định các điểm \(E,\,F\), biết rằng \[\overrightarrow {CE} = 3\overrightarrow {AB} - 4\overrightarrow {AC} \], \[\overrightarrow {AF} + 2\overrightarrow {BF} - 4\overrightarrow {CF} = \overrightarrow 0 \].
(1 điểm) Cho hình thang vuông \(ABCD\) đường cao \[AB = h,\] cạnh đáy \[AD = a,BC = b.\] Tìm điều kiện giữa \(a,\,\,b,\,\,h\) để
a) \(AC\) và \(DB\) vuông góc.
b) \[\widehat {AIB} = 90^\circ \] với \(I\) là trung điểm \(CD\).
(1 điểm) Kiểm tra chiều dài của 10 con cá voi xanh trưởng thành được kết quả như sau (đơn vị: mét)
26 25 27 27 33 26 24 26 21 31.
a) Hãy tìm số trung bình, khoảng biến thiên, khoảng tứ phân vị, độ lệch chuẩn của mẫu số liệu trên.
b) Xác định các giá trị bất thường (nếu có) của mẫu số liệu trên.








