Bộ 10 đề thi cuối kì 1 Toán 10 Kết nối tri thức có đáp án - Đề 4
38 câu hỏi
I. Trắc nghiệm (7 điểm)
Cho hai mệnh đề
\(P\): “\(n\) là số tự nhiên chẵn”, \(Q\): “\(n\) chia hết cho 2”.
Mệnh đề \(P \Rightarrow Q\) được phát biểu là
“Nếu \(n\) chia hết cho 2 thì \(n\) là số tự nhiên chẵn”;
“Nếu \(n\) là số tự nhiên chẵn thì \(n\) chia hết cho 2”;
“\(n\) là số tự nhiên chẵn chia hết cho 2”;
“\(n\) là số tự nhiên thì \(n\) chẵn và chia hết cho 2”.
Cho \(A = \left\{ {0;\,\,1;\,\,2;\,\,3;\,\,4} \right\},\,B = \left\{ {2;\,\,3;\,\,4;\,\,5;\,\,6} \right\}\). Tập hợp \(A\backslash B\) bằng
\(\left\{ {1;\,\,5} \right\}\);
\(\left\{ 0 \right\}\);
\(\left\{ {1;\,\,2} \right\}\);
\(\left\{ {0;\,\,1} \right\}\).
Dạng liệt kê của tập hợp \[A = \left\{ {3k|k \in \mathbb{Z}, - 2 < k \le 3} \right\}\]là:
\[\left\{ { - 2; - 1;\,\,0;\,\,1;\,\,2;\,\,3} \right\}\];
\[\left\{ { - 6;\, - 3;\,\,0;\,\,3;\,\,6;\,\,9} \right\}\];
\[\left\{ { - 3;\,\,0;\,\,3;\,\,6;\,\,9} \right\}\];
\[\left\{ { - 1;\,\,0;\,\,1;\,\,2;\,\,3} \right\}\].
Một gian hàng trưng bày giường và tủ quần áo rộng 95 m2. Diện tích để kê một chiếc giường là 3,2 m2, một chiếc tủ quần áo là 1,6 m2. Gọi \(x\) là số chiếc giường và \(y\) là số chiếc tủ quần áo được kê. Viết bất phương trình bậc nhất hai ẩn \(x,\,y\) cho phần mặt sàn để kê giường và tủ quần áo biết diện tích mặt sàn dành cho lưu thông tối thiểu là 15 m2.
\(32x + 16y \ge 80\);
\(2x + y \le 50\);
\(2x + y \ge 50\);
\(2x + y < 50\).
Cho hệ bất phương trình \(\left\{ \begin{array}{l}x + y - 2 \le 0\\2x - 3y + 2 > 0\end{array} \right.\). Trong các điểm sau, điểm nào không thuộc miền nghiệm của hệ bất phương trình trên?
\(O\left( {0;\,\,0} \right)\);
\[M\left( {1;\,\,1} \right)\];
\[N\left( { - 1;\,\,1} \right)\];
\[P\left( { - 1;\,\, - 1} \right)\].
Cho tam giác \(ABC\) vuông cân tại \(A\). Khi đó \(\sin B\) bằng
0;
\(\frac{{\sqrt 2 }}{2}\);
\(\frac{{\sqrt 3 }}{2}\);
1.
Cho \(\alpha \) và \(\beta \) là hai góc khác nhau và bù nhau. Trong các đẳng thức sau đây, đẳng thức nào sai?
\(\sin \alpha = \sin \beta \);
\(\cot \alpha = \cot \beta \);
\(\tan \alpha = - \tan \beta \);
\(\cos \alpha = - \cos \beta \).
Cho biết \(\tan \alpha = - 3.\) Giá trị của \(P = \frac{{6\sin \alpha - 7\cos \alpha }}{{6\cos \alpha + 7\sin \alpha }}\) bằng bao nhiêu ?
\(P = \frac{4}{3}\);
\(P = \frac{5}{3}\);
\(P = - \frac{4}{3}\);
\(P = - \frac{5}{3}\).
Cho \(\Delta ABC\) có \(AB = 10,\,BC = 21,\,CA = 17\). Số đo góc lớn nhất trong tam giác xấp xỉ bằng
\(90^\circ \);
\(98^\circ \);
\(99^\circ \);
\(100^\circ \).
Phát biểu nào sau đây là sai?
Hai vectơ cùng hướng thì cùng phương;
Hai vectơ cùng phương thì cùng hướng;
Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối;
Vectơ là đoạn thẳng có hướng.
Cho tam giác đều \(ABC\). Hãy chỉ ra đẳng thức đúng trong các đẳng thức sau:
\(\overrightarrow {AB} = \overrightarrow {BA} \);
\(\left| {\overrightarrow {AB} } \right| = - \left| {\overrightarrow {BA} } \right|\);
\(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {AC} } \right|\);
\(\overrightarrow {AB} = \overrightarrow {AC} \).
Cho ba điểm phân biệt \(A,\;B,\;C\). Đẳng thức nào sau đây đúng?
\(\overrightarrow {CA} + \overrightarrow {AB} = \overrightarrow {BC} \);
\[\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {BC} \];
\(\overrightarrow {AB} + \overrightarrow {CA} = \overrightarrow {CB} \);
\(\overrightarrow {AB} - \overrightarrow {BC} = \overrightarrow {CA} \).
Gọi \(O\) là tâm hình bình hành \(ABCD\). Đẳng thức nào sau đây sai?
\(\overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {CD} \);
\(\overrightarrow {OB} - \overrightarrow {OC} = \overrightarrow {OD} - \overrightarrow {OA} \);
\(\overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {DB} \);
\(\overrightarrow {BC} - \overrightarrow {BA} = \overrightarrow {DC} - \overrightarrow {DA} \).
Cho tam giác \(ABC\) vuông cân đỉnh \(C\), \[AB = \sqrt 2 \]. Độ dài của \[\overrightarrow {AB} + \overrightarrow {AC} \] là
\[\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \sqrt 5 \];
\[\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = 2\sqrt 5 \];
\[\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \sqrt 3 \];
\[\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = 2\sqrt 3 \].
Gọi \(G\) là trọng tâm của tam giác \(ABC,\,I\) là trung điểm của cạnh \(BC\). Khẳng định nào sau đây là sai?
\(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \);
\(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \) với \(M\)là điểm bất kỳ;
\(\overrightarrow {AG} = \frac{2}{3}\overrightarrow {AI} \);
\(\overrightarrow {GA} = 2\overrightarrow {GI} \).
Cho tam giác \(ABC\) và điểm \(M\) thỏa mãn \(\overrightarrow {MA} + 2\overrightarrow {MB} = \overrightarrow {CB} \). Khi đó
\(M\) là trọng tâm của tam giác \(ABC\);
\(M\) là trung điểm cạnh \(AC\);
\(M\) là đỉnh của hình bình hành \(ABMC\);
\(M\) là trung điểm cạnh \(AB\).
Cho tứ giác \(ABCD,\,\,O\) là giao điểm của hai đường chéo \(AC\) và \(BD\). Gọi \(G\) và \(G'\) theo thứ tự là trọng tâm của tam giác \(OAB\) và \(OCD\). Khi đó \(\overrightarrow {GG'} \) bằng
\(\frac{2}{3}\left( {\overrightarrow {AC} + \overrightarrow {BD} } \right)\);
\(\frac{1}{3}\left( {\overrightarrow {AC} + \overrightarrow {BD} } \right)\);
\(\frac{1}{2}\left( {\overrightarrow {AC} + \overrightarrow {BD} } \right)\);
\(3\left( {\overrightarrow {AC} + \overrightarrow {BD} } \right)\).
Đẳng thức nào sau đây mô tả đúng hình vẽ dưới?

\[\overrightarrow {AI} = \frac{1}{3}\overrightarrow {AB} \];
\[\overrightarrow {AI} = - \frac{1}{3}\overrightarrow {AB} \];
\[\overrightarrow {AI} = 3\overrightarrow {AB} \];
\[\overrightarrow {AI} = - 3\overrightarrow {AB} \].
Trong mặt phẳng tọa độ \[Oxy\], cho vectơ \(\overrightarrow u = \,2\overrightarrow i + 13\overrightarrow j \). Tọa độ của vectơ \(\overrightarrow u \) là
\(\overrightarrow u = \left( {2;\,13} \right)\);
\(\overrightarrow u = \left( {2;\, - 13} \right)\);
\(\overrightarrow u = \left( { - \,2;\, - 13} \right)\);
\(\overrightarrow u = \left( { - \,2;\,13} \right)\).
Trong mặt phẳng tọa độ \(Oxy\), cho hai điểm \(M\left( { - 1;\,\,2} \right)\) và \(N\left( {3;\, - 1} \right)\). Tọa độ của vectơ \(\overrightarrow {NM} \) là
\(\overrightarrow {NM} = \left( {4;\,\, - 3} \right)\);
\(\overrightarrow {NM} = \left( {2;\,\,1} \right)\);
\(\overrightarrow {NM} = \left( { - 4;\,3} \right)\);
\(\overrightarrow {NM} = \left( {2;\,\, - 1} \right)\).
Trong mặt phẳng tọa độ \(Oxy\), cho 3 điểm \(A\left( { - 2; - 3} \right),B\left( {1;4} \right),C\left( {3;1} \right)\). Đặt \(\overrightarrow v = \overrightarrow {AB} + \overrightarrow {AC} \). Hỏi tọa độ \(\overrightarrow v \) là cặp số nào?
\(\left( {6;0} \right)\);
\(\left( {0; - 1} \right)\);
\(\left( { - 8;\,\,11} \right)\);
\(\left( {8;\,\,11} \right)\).
Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) khác vectơ \(\overrightarrow 0 \). Tích vô hướng của hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) là một số thực được xác định bởi
\(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot \sin \left( {\overrightarrow a ,\,\overrightarrow b } \right)\);
\(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot \cos \left( {\overrightarrow a ,\,\overrightarrow b } \right)\);
\(\overrightarrow a \cdot \overrightarrow b = - \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot \sin \left( {\overrightarrow a ,\,\overrightarrow b } \right)\);
\(\overrightarrow a \cdot \overrightarrow b = - \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot \cos \left( {\overrightarrow a ,\,\overrightarrow b } \right)\).
Cho \(\overrightarrow a \) và \(\overrightarrow b \) là hai vectơ vuông góc với nhau. Mệnh đề nào sau đây đúng?
\(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right|\);
\(\overrightarrow a \cdot \overrightarrow b = 0\);
\(\overrightarrow a \cdot \overrightarrow b = - 1\);
\(\overrightarrow a \cdot \overrightarrow b = - \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right|\).
Tam giác \(ABC\) vuông ở \(A\) và có \[BC = 2AC.\] Tính \(\cos \left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right).\)
\(\cos \left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right) = \frac{1}{2}\) ;
\(\cos \left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right) = - \frac{1}{2}\);
\(\cos \left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right) = \frac{{\sqrt 3 }}{2}\);
\(\cos \left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right) = - \frac{{\sqrt 3 }}{2}\).
Cho tam giác \(ABC\) vuông tại \(C\) có \(AC = 9\), \(BC = 5\). Tích vô hướng \(\overrightarrow {AB} \cdot \overrightarrow {AC} \) bằng
81;
91;
56;
76.
Số quy tròn của số gần đúng \(a\) trong trường hợp \(\overline a = 37\,\,975\,\,421 \pm 150\) là
37 975 000;
3 797 600;
3 797 000;
37 975 400.
Làm tròn số 5,1232 đến hàng phần trăm. Sai số tuyệt đối của số quy tròn là
0,0032;
– 0,0032;
0,03;
Đáp án khác.
Số đặc trưng nào sau đây không đo xu thế trung tâm của mẫu số liệu?
Phương sai;
Số trung bình;
Mốt;
Số trung vị.
Điều tra tiền lương hằng tháng của 100 công nhân tại phân xưởng \(A\) cho kết quả như sau:
Tiền lương (triệu đồng) | 5 | 6 | 7 | 8 | 9 | 9,5 |
Tần số | 26 | 34 | 20 | 10 | 5 | 5 |
Giá trị mốt của mẫu số liệu trên là
5;
6;
7,5;
9,5.
Tiền lương trung bình của mỗi công nhân trong Câu 29 là
6;
6,46;
6,465;
6,47.
Cho mẫu số liệu: 1; 1; 2; 7; 8; 9; 10; 12; 16. Trung vị của mẫu số liệu là
8;
8,5;
7,3;
7,5.
Khoảng tứ phân vị \({\Delta _Q}\) cho biết
mức độ phân tán của 25% số liệu dưới của mẫu số liệu đã sắp xếp;
mức độ phân tán của 50% số liệu trên của mẫu số liệu đã sắp xếp;
mức độ phân tán của 50% số liệu chính giữa của mẫu số liệu đã sắp xếp;
mức độ phân tán của 25% số liệu chính giữa của mẫu số liệu đã sắp xếp.
Một tổ gồm 10 học sinh có điểm kiểm tra môn Toán giữa học kì 1 như sau: 5; 6; 8; 5; 8; 9; 7; 7; 9; 8. Khoảng biến thiên của mẫu số liệu trên là
4;
14;
7;
10.
Phương sai của mẫu số liệu trong Câu 33 xấp xỉ bằng
1,69;
1,96;
1,4;
1,3.
Khoảng tứ phân vị của mẫu số liệu ở Câu 33 là
1,5;
2;
2,5;
3.
II. Tự luận (3 điểm)
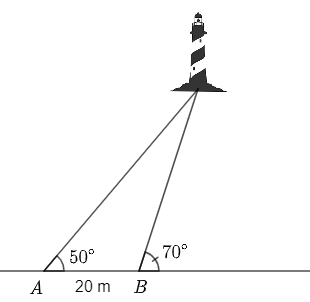
(1 điểm) Một người đi dọc bờ biển từ vị trí \(A\) đến vị trí \(B\) và quan sát một ngọn hải đăng. Góc nghiêng của phương quan sát từ vị trí \(A,\,\,B\) tới ngọn hải đăng với đường đi của người quan sát là \(50^\circ \) và \(70^\circ \). Biết khoảng cách giữa hai vị trí \(A\) và \(B\) là 20 m. Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
(1 điểm) Cho tam giác \(ABC\) có \[\,AB = c,BC = a,\,CA = b\]. Trung tuyến \(CM\) vuông góc với phân giác trong \(AL\) và \[\frac{{CM}}{{AL}} = \frac{{\sqrt 3 }}{2}\]. Tính \[\cos A\].
(1 điểm) Bảng sau ghi giá bán ra lúc 15 giờ của hai mã cổ phiếu \(M\) và \(N\) trong 10 ngày liên tiếp (đơn vị: nghìn đồng).
Ngày | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
\(M\) | 25 | 25,1 | 25,3 | 15,5 | 25,6 | 25,5 | 25,4 | 25,5 | 25,4 | 25,2 |
\(N\) | 27 | 27,4 | 27,8 | 48,2 | 29 | 28,8 | 28,8 | 28,8 | 28,6 | 29,2 |
a) Biết có 1 trong 10 ngày trên có sự bất thường trong giá cổ phiếu. Hãy tìm ngày đó và giải thích.
b) Sau khi bỏ đi ngày có giá trị bất thường, hãy cho biết giá cổ phiếu nào ổn định hơn. Tại sao?








