Bộ 5 đề thi giữa kì Toán 10 Kết nối tri thức cấu trúc mới (có tự luận) có đáp án - Đề 1
21 câu hỏi
Cho mệnh đề là số lẻ”, mệnh đề phủ định của mệnh đề A là:
là số lẻ”.
là số chẵn”.
là số lẻ”.
là số chẵn”.
Cho hai tập hợp \(A = \left\{ {1;2;3} \right\}\) và \(B = \left\{ {1;2} \right\}.\) Khẳng định nào sau đây là đúng?
\(B \subset A.\)
\(A \subset B.\)
\(A = B.\)
\(A \in B.\)
Cho \(A = \left[ { - 5;\,\,1} \right]\) và \(B = \left( { - 3;\,\,2} \right)\). Tập hợp \(A \cup B\) chứa bao nhiêu số nguyên âm?
\(7\).
\(6\).
\(4\).
\(5\).
Cho bất phương trình \(2x + y > 6\). Khẳng định nào sau đây là đúng?
Bất phương trình đã cho có nghiệm duy nhất.
Bất phương trình đã cho vô nghiệm.
Bất phương trình đã cho có vô số nghiệm.
Bất phương trình đã cho có tập nghiệm là \(\left[ {3; + \infty } \right)\).
Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn?
\(\left\{ \begin{array}{l}x + y > 1\\2x - y < 2\end{array} \right..\)
\(\left\{ \begin{array}{l}{x^2} + y > 1\\2x - y < 2\end{array} \right..\)
\(\left\{ \begin{array}{l}x + y > 1\\2{x^2} - y < 2\end{array} \right..\)
\(\left\{ \begin{array}{l}x + {y^2} > 1\\2x - y < 2\end{array} \right..\)
Cặp số \(\left( {x;y} \right)\) nào dưới đây là một nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{x + y > 2}\\{ - 2x + y \le 7}\end{array}} \right.\)?
\(\left( { - 1;12} \right)\).
\(\left( { - 5; - 2} \right)\).
\(\left( {2; - 5} \right)\).
\(\left( {4; - 1} \right)\).
Cho góc \(\alpha \) là góc tù. Khẳng định nào sau đây là đúng?
\(\tan \alpha < 0\).
\(\sin \alpha < 0\).
\(\cos \alpha > 0\).
\(\cot \alpha > 0\).
Trong các đẳng thức sau đây, đẳng thức nào đúng?
\(\sin \left( {180^\circ - \alpha } \right) = - \sin \alpha \).
\(\cos \left( {180^\circ - \alpha } \right) = \cos \alpha \).
\(\tan \left( {180^\circ - \alpha } \right) = \tan \alpha \).
\(\cot \left( {180^\circ - \alpha } \right) = - \cot \alpha \).
Cho tam giác \(ABC\) (theo hình dưới đây) có \(a = 6, b = 10\), góc \(C\) bằng \(60^\circ \).
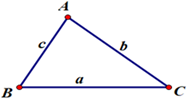
Độ dài cạnh \(c\)bằng
\(c = 14\).
\(c = 2\sqrt {19} \).
\(c = \sqrt {106} \).
\(c = 4\).
Cho mệnh đề \[P\]: “Nếu \[a + b < 2\] thì một trong hai số \[a\] và \[b\] nhỏ hơn 1”. Mệnh đề nào sau đây tương đương với mệnh đề đã cho?
Điều kiện đủ để một trong hai số \[a\] và \[b\] nhỏ hơn 1 là \[a + b < 2\].
Điều kiện cần để một trong hai số \[a\] và \[b\] nhỏ hơn 1 là \[a + b < 2\].
Điều kiện đủ để \[a + b < 2\] là một trong hai số \[a\] và \[b\] nhỏ hơn 1.
Cả B và C.
Phần không bị gạch chéo trong hình vẽ dưới đây biểu diễn miền nghiệm của bất phương trình nào?
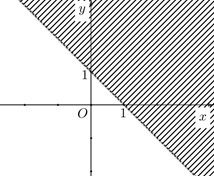
\(x + y < 1.\)
\(x + y > 1.\)
\(x + y < 2.\)
\(x + y > 2.\)
Cho biết \(\tan \alpha = 2\). Giá trị của \(M = \frac{{10\sin \alpha + 11\cos \alpha }}{{4\sin \alpha + 7\cos \alpha }}\) bằng
Cho mệnh đề \(P\): “Tam giác \(ABC\) vuông tại \(A\)” và mệnh đề \(Q:\) “Tam giác \(ABC\) có \(AB{}^2 + A{C^2} = B{C^2}\)”. Xét mệnh đề kéo theo \(P \Rightarrow Q\).
a) Mệnh đề \(P \Rightarrow Q\) được phát biểu là: “Nếu tam giác \(ABC\) vuông tại \(A\) thì tam giác \(ABC\) có \(AB{}^2 + A{C^2} = B{C^2}\)”.
b)\(P\) là điều kiện cần để có \(Q\).
c) Mệnh đề \(P \Rightarrow Q\) là mệnh đề đúng.
d) Mệnh đề đảo của mệnh đề \(P \Rightarrow Q\) là mệnh đề sai.
Cho tam giác \[ABC\] có \[AC = 10,\,\,BC = 12,\,\,\widehat B = 45^\circ \].
a) Công thức tính bán kính của đường tròn ngoại tiếp \(\Delta ABC\) là \(R = \frac{{BC}}{{2\sin B}}\).
b) \(\sin A = \frac{{5\sqrt 2 }}{{12}}\).
c) Bán kính đường tròn ngoại tiếp \(\Delta ABC\) là \(5\sqrt 2 \).
d) \(\frac{{3BC - 2AC - AB}}{{6\sin A - 4\sin B - 2\sin C}} = \frac{{2\sqrt 5 }}{5}\).
Cho hai tập hợp \(A = \left[ { - 2;3} \right] \cup \left[ {5;10} \right)\), \(B = \left( {1; + \infty } \right)\) . Biết \(A \cap B\)=\(\left( {a;b} \right] \cup \left[ {c;d} \right)\) với \(a,b,c,d\) là các số nguyên dương. Khi đó \(a + b + c + d\) bằng bao nhiêu?
Phần nửa mặt phẳng bờ \(d\) không bị gạch ở hình vẽ sau là miền nghiệm của bất phương trình \(x + my \ge n\).
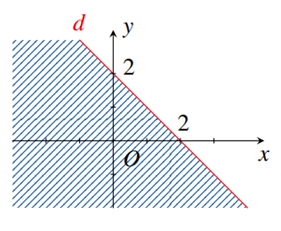
Giá trị của biểu thức \(S = 3m + n\) bằng bao nhiêu?
Cho \(\cot \alpha = - \sqrt 2 \) và \(P = \frac{{2\sin \alpha - \sqrt 2 \cos \alpha }}{{4\sin \alpha + 3\sqrt 2 \cos \alpha }}\). Tính giá trị biểu thức \(A = {m^2} - {n^2}\) biết \(P = \frac{m}{n}\) \((m \in \mathbb{Z},n \in \mathbb{N}\) và \(\frac{m}{n}\) là phân số tối giản).
Hai tàu du lịch xuất phát từ hai thành phố cảng \(A\) và \(B\) cách nhau \(200\,\,{\rm{(km)}}\) đến đảo \(C\) như hình minh họa.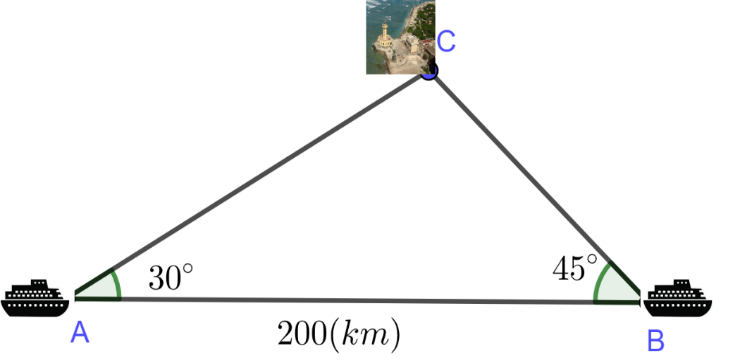
Biết Tàu 1 ở thành phố \(A\) khởi hành lúc 8 giờ và chuyển động đều với vận tốc \[80\,\,{\rm{(km/h)}}\]. Tàu 2 ở thành phố \(B\) muốn đến đảo \(C\) cùng lúc với tàu 1 thì phải khởi hành lúc \(a\) giờ \(b\) phút (làm tròn đến đơn vị phút), biết tàu 2 chuyển động đều cùng vận tốc \(80\,{\rm{(km/h)}}.\) Tính \(a + b.\)
Lớp 10E1 có 35 học sinh làm bài kiểm tra thường xuyên môn Toán. Đề bài gồm 3 bài toán. Sau khi kiểm tra cô giáo tổng hợp được kết quả như sau: có 12 học sinh chỉ giải được bài toán thứ nhất, 14 học sinh giải được bài toán thứ hai, 15 học sinh giải được bài toán thứ ba, 3 học sinh chỉ giải được bài toán thứ hai và thứ ba. Hỏi lớp 10E1 có bao nhiêu học sinh giải được cả 3 bài toán biết rằng mỗi học sinh đều làm được ít nhất một bài?
Một xưởng sản xuất đồ gỗ mỹ nghệ sản suất ra hai bộ sản phẩm loại \[I\] và loại \[II\]. Mỗi bộ sản phẩm loại \[I\] lãi \[5\] triệu đồng, mỗi bộ sản phẩm loại \[II\] lãi \[4\] triệu đồng. Để sản suất mỗi bộ sản phẩm loại \[I\] cần máy làm việc trong \[3\] giờ và nhân công làm việc trong \[2\] giờ. Để sản suất mỗi bộ sản phẩm loại \[II\] cần máy làm việc trong \[3\] giờ và nhân công làm việc trong \[1\] giờ. Biết rằng chỉ dùng máy hoặc chỉ dùng nhân công không thể đồng thời làm hai loại sản phẩm cùng lúc, số nhân công luôn ổn định. Một ngày máy làm việc không quá \[15\]giờ, nhân công làm việc không quá \[8\] giờ. Tính số tiền lãi lớn nhất xưởng đó đạt được trong một ngày nếu bán hết toàn bộ sản phẩm làm ra.
Người ta cần trang trí một họa tiết như hình vẽ bằng cách sơn kín phần được tô đậm. Biết chi phí để sơn 1 mét vuông là 250 nghìn đồng, tam giác trong hình vẽ có các cạnh lần lượt là 3 mét, 5 mét, 5 mét. Hỏi số tiền cần bỏ ra là bao nhiêu nghìn đồng để hoàn thành việc sơn trang trí họa tiết đó (làm tròn kết quả đến hàng đơn vị).








