Bộ 5 đề thi giữa kì 2 Toán 8 Kết nối tri thức có đáp án (Đề 2)

Cho biểu thức: \(D = \left( {\frac{{x + 2}}{{3x}} + \frac{2}{{x + 1}} - 3} \right):\frac{{2 - 4x}}{{x + 1}} - \frac{{3x - {x^2} + 1}}{{3x}}.\)

a) Viết điều kiện xác định của biểu thức \[D.\]

b) Rút gọn biểu thức \(D.\)

c) Tính giá trị của biểu thức \[D\] biết \(\left( {2x - 1} \right)\left( {{x^2} + 1} \right) = 0.\)

Giải các phương trình sau:

a) \(\frac{2}{3}x + 2\frac{1}{2} = 0\).  b) \(x - 4x + 2x - 29 = 4x + 1\).

c) \(\frac{{2x - 1}}{3} - \frac{{x + 7}}{4} = \frac{{5 - 3x}}{2}\).  d) \[2x\left( {x--1} \right) = {x^2} - 1.\]

Một tàu hỏa từ Hà Nội đi Thành phố Hồ Chí Minh. Sau 1 giờ 48 phút, một tàu hỏa khác khởi hành từ Nam Định cũng đi Thành phố Hồ Chí Minh với vận tốc nhỏ hơn vận tốc của tàu thứ nhất \[5{\rm{ km/h}}.\] Hai tàu gặp nhau tại một nhà ga sau 4 giờ 48 phút kể từ khi tàu thứ nhất khởi hành. Tính vận tốc của mỗi tàu, biết rằng ga Nam Định nằm trên đường từ Hà Nội đi Thành phố Hồ Chí Minh và cách ga Hà Nội 87 km.

Cho tam giác \(ABC\) vuông tại \(A\) có \[AB = 6\,\,{\rm{cm}}\] và \[AC = 8\,\,{\rm{cm}}.\] Đường phân giác của góc \(ABC\) cắt cạnh \(AC\)tại \(D.\) Từ \(C\) kẻ \(CE \bot BD\) tại \(E.\)

a) Tính độ dài \(BC\) và tỉ số \(\frac{{AD}}{{DC}}.\)

b) Chứng minh  Từ đó suy ra \(BD \cdot EC = AD \cdot BC.\)

c) Chứng minh \(\frac{{CD}}{{BC}} = \frac{{CE}}{{BE}}.\)

d) Gọi \(EH\) là đường cao \(\Delta EBC.\) Chứng minh \(CH \cdot HB = ED \cdot EB.\)

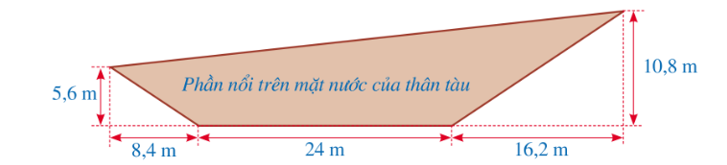
Một chiếc tàu thủy có mặt cắt dọc phần nổi trên mặt nước của thân tàu được mô tả ở hình bên dưới. Tính chu vi mặt cắt dọc nổi trên mặt nước của thân tàu đó (làm tròn kết quả đến hàng phần mười của mét).