Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 7)

b) Rút gọn biểu thức \(P\).

c) Tìm giá trị của biểu thức \(P\) tại \(x = \frac{1}{2}\).

Để sử dụng dịch vụ truyền hình cáp, người dùng phải trả một khoản phí ban đầu và phí thuê bao hàng tháng. Một phần đường thẳng \(d\) ở hình dưới đây biểu thị chi phí (đơn vị: triệu đồng) để sử dụng dịch vụ truyền hình cáp theo thời gian sử dụng của một gia đình (đơn vị: tháng).

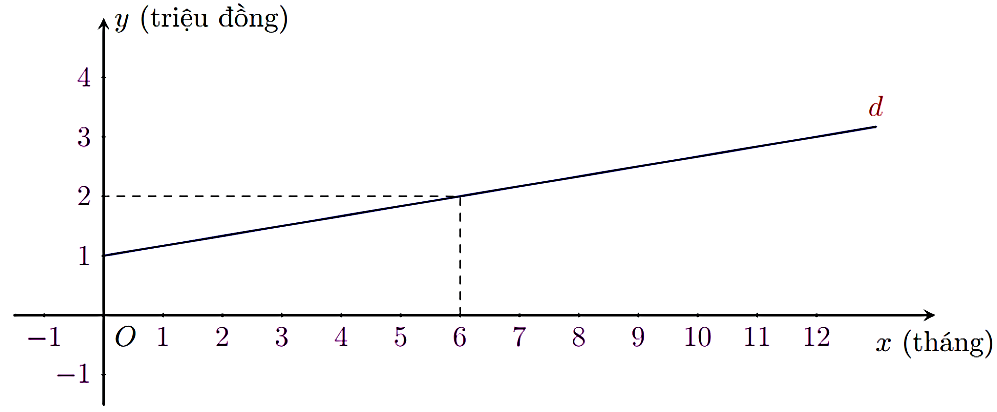
a) Tìm hàm số bậc nhất sao cho đồ thị của hàm số là đường thẳng \(d.\)

b) Giao điểm của đường thẳng \(d\) với trục tung trong tình huống này có ý nghĩa gì? Tính tổng chi phí mà gia đình đó phải trả khi sử dụng dịch vụ truyền hình cáp với thời gian 12 tháng.

Một hình chữ nhật có chu vi bằng \[132\,\,m\]. Nếu tăng chiều dài thêm \[8\,\,m\] và giảm chiều rộng đi \[4\,\,m\]thì diện tích hình chữ nhật tăng thêm \[52\,\,{m^2}\]. Tính các kích thước của hình chữ nhật.

a) Tính xác suất thực nghiệm của biến cố “Mặt xuất hiện của xúc xắc là số 4”.

b) Tính xác suất thực nghiệm của biến cố “Mặt xuất hiện của xúc xắc là số lẻ”.

c) Nêu mối liên hệ giữa xác suất thực nghiệm của biến cố “Mặt xuất hiện của xúc xắc là số lẻ” với xác suất của biến cố đó khi số lần gieo ngày càng lớn.

a) Chứng minh: $\mathrm{\Delta ABK}\backsim \mathrm{\Delta CBF}$.

b) Chứng minh: \(AE \cdot AC = AF \cdot AB\).

c) Gọi \[N\] là giao điểm của \[AK\] và \[EF,{\rm{ }}D\] là giao điểm của đường thẳng \[BC\] và đường thẳng \[EF\] và \[O,{\rm{ }}I\] lần lượt là trung điểm của \[BC\] và  \[AH.\] Chứng minh \[ON\] vuông góc \[DI.\]

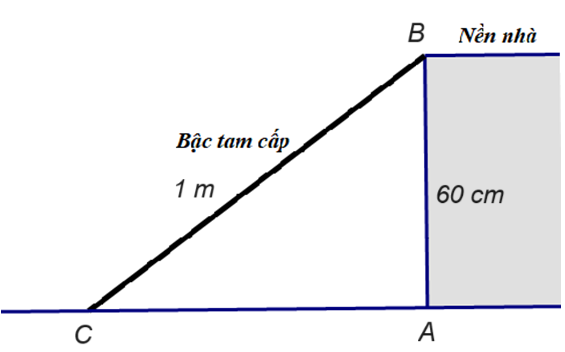
Theo quy định của khu phố, mỗi gia đình sử dụng bậc tam cấp di động để dắt xe vào nhà không được lấn chiếm vỉa hè quá \[85{\rm{ cm}}\]ra phía vỉa hè. Biết rằng nhà bạn Nam có nền cao \[60{\rm{ cm}}\]so với vỉa hè và có chiều dài bậc tam cấp là \[1{\rm{ m}}.\] Theo em, nhà bạn Nam có thực hiện đúng quy định của khu phố không? Vì sao?

Cho hình chóp tam giác đều \(S.ABC,\) có cạnh đáy \(AB = 5{\rm{\;cm}}\) và độ dài trung đoạn \(SI = 6{\rm{\;cm}}\) (hình vẽ bên). Tính diện tích xung quanh và diện tích toàn phần của hình chóp \(S.ABC.\)

(Làm tròn các kết quả đến chữ số thập phân thứ hai)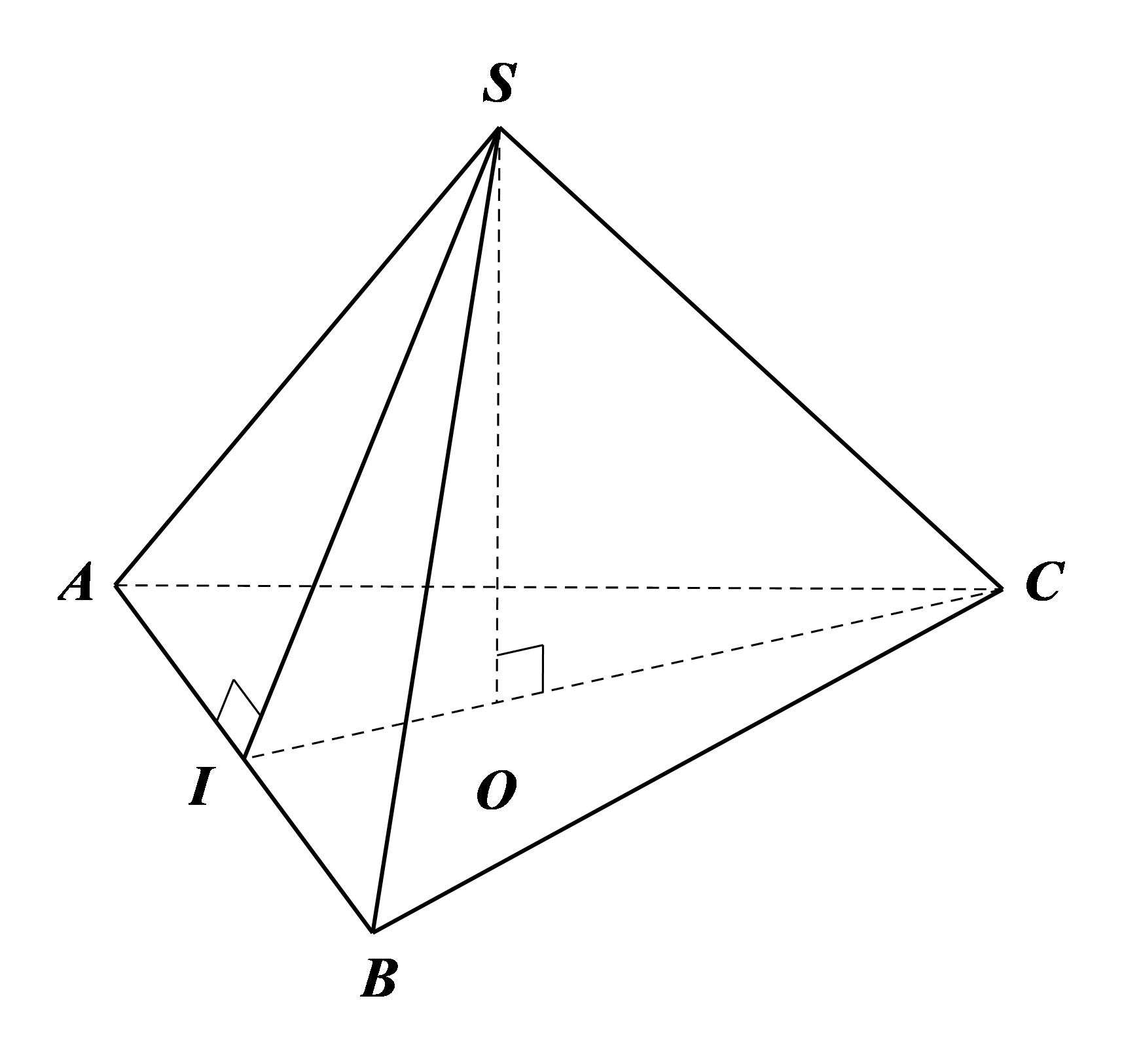

(0,5 điểm)Tronghộp kín có 6 viên bi đỏ, 3 viên bi xanh, các viên bi có cùng kích thước, khối lượng và hình dạng như nhau, chỉ khác màu sắc. Lấy ngẫu nhiên 1 viên bi từ trong hộp. Sau đó, thêm mỗi hộp một số viên bi màu đỏ, màu xanh sao cho xác suất chọn được viên bi mỗi màu không đổi. Hỏi cần thêm ít nhất bao nhiêu viên bi mỗi màu?