Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 11)
29 câu hỏi
Phần 1. (3,0 điểm) Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Biểu thức nào sau đây không phải là một phân thức đại số?
\(\frac{{3x}}{y}.\)
\(\frac{3}{{x + 4}}.\)
\(\frac{1}{2}x + 1.\)
\(\frac{{x - 2}}{0}.\)
Mẫu thức chung của hai phân thức \(\frac{1}{{2{x^2}y}}\) và \(\frac{1}{{3x{y^2}}}\) là
\(6xy.\)
\(6{x^2}y.\)
\(6x{y^2}.\)
\(6{x^2}{y^2}.\)
Phương trình nào sau đây là phương trình bậc nhất một ẩn?
\({y^2} + 8x - 2022 = 0.\)
\(3x + 6 = 0.\)
\(3x - 2y - 9 = 0.\)
\(2{x^2} - 4 = 0.\)
Gọi \(x\) (km) là chiều dài quãng đường \(AB\). Biểu thức biểu thị thời gian một xe máy đi từ \(A\) đến \(B\) với vận tốc \(40\) (lm/h) là
\(40 - x.\)
\(\frac{x}{{40}}.\)
\(40x.\)
\(40 + x.\)
Trong các hàm số sau, hàm số nào là hàm số bậc nhất?
\(y = {x^2} + 1.\)
\(y = 2\sqrt x + 1.\)
\(y = \frac{2}{3} - 2x.\)
\(y = 1 - \frac{1}{x}.\)
Biết rằng đồ thị hàm số \(y = 2x + 1\) và đồ thị hàm số \(y = ax + 3\) là hai đường thẳng song song, khi đó hệ số \(a\) bằng
\(1.\)
\(2.\)
\(3.\)
\(0.\)
Một túi đựng các viên bi có hình dạng như nhau, chỉ khác màu. Trong đó có \(5\) viên bi màu đỏ, \(6\) viên bi màu xanh và \(3\) viên bi màu vàng. Lấy ngẫu nhiên một viên bi trong túi. Số kết quả có thể xảy ra là
\(6.\)
\(14.\)
\(3.\)
\(5.\)
Chọn ngẫu nhiên một số tự nhiên có một chữ số. Số kết quả có thể xảy ra là
\(7.\)
\(9.\)
\(10.\)
\(8.\)
Cho biết . Khi đó số đo góc D bằng
\(50^\circ .\)
\(60^\circ .\)
\(70^\circ .\)
\(80^\circ .\)
Nếu theo tỉ số thì theo tỉ số
\(\frac{3}{2}.\)
\(\frac{9}{4}.\)
\(\frac{4}{3}.\)
\(\frac{2}{3}.\)
Cho hình chóp tứ giác đều \(S.ABCD\) như hình vẽ trên.
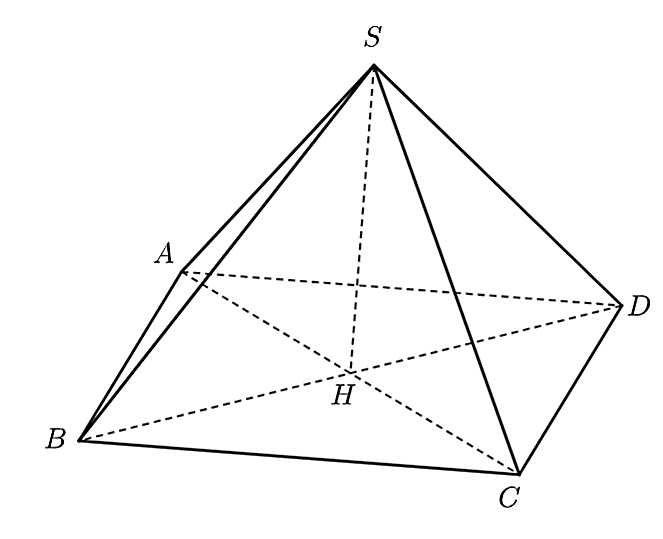
Khi đó, \(SH\) được gọi là
đường cao.
cạnh bên.
cạnh đáy.
đường chéo.
Hình chóp tam giác đều có
4 mặt, 4 cạnh.
6 mặt, 4 cạnh.
4 mặt, 6 cạnh.
6 mặt, 6 cạnh.
a) Hai đường thẳng luôn cắt nhau với mọi giá trị của \(m.\)
b) Với \(m = - 4\) thì chỉ đường thẳng \(\left( d \right)\) đi qua điểm \(A\left( {1;0} \right)\).
c) Với \(m = 4\) thì hai đường thẳng cắt nhau tại điểm \(\left( {\frac{6}{7};\frac{4}{7}} \right).\)
d) Điều kiện của \(m\) để hai đường thẳng \(\left( d \right),\left( {d'} \right)\) cắt nhau tại 1 điểm nằm bên phải trục tung là \(m < 1.\)
a) Có \(6\) kết quả có thể xảy ra.
b) Có \(3\) kết quả thuận lợi cho biến cố “Mặt xuất hiện trên xúc xắc có số chấm là số chia hết cho \(2\)”.
c) Xác suất của biến cố “Mặt xuất hiện trên con xúc xắc có số chấm là số chia hết cho \(3\)” là \(0,5.\)
d) Xác suất của biến cố “Mặt xuất hiện trên con xúc xắc có số chấm là số chia hết cho \(5\) dư 1” là \(\frac{1}{3}.\)
Phần 3. (2,0 điểm) Câu hỏi trắc nghiệm trả lời ngắn
Trong các câu từ 15 đến 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Xác định hệ số góc của đường thẳng đi qua hai điểm \(A\left( {1;2} \right)\) và \(B\left( {3;4} \right)\).
Bạn Cường vào cửa hàng Lotteria và dự định mua một suất gà rán. Khi đọc menu, bạn Cường thấy cửa hàng đang có các món như sau: combo gà rán (ưu đãi) có giá \(97{\rm{ }}000\) đồng, combo gà viên (ưu đãi) có giá \({\rm{84 }}000\) đồng, gà rán – 1 miếng có giá \({\rm{35 }}000\)đồng, gà rán – 2 miếng có giá \({\rm{68 }}000\) đồng, gà rán – 3 miếng có giá \({\rm{101 }}000\) đồng, cánh gà chiên – 3 miếng có giá \({\rm{48 }}000\) nghìn đồng. Bạn Cường cảm thấy món nào cũng ngon và dự định sẽ nhắm mắt chỉ tay chọn ngẫu nhiên một món. Tính xác suất “Món gà được bạn Cường chọn có giá dưới \({\rm{70 }}000\) đồng”. (Kết quả ghi dưới dạng số thập phân)
Gấp mảnh giấy hình chữ nhật như hình vẽ sau đây sao cho điểm \(D\) trùng với điểm \(E\), là một điểm nằm trên cạnh \(BC\). Biết rằng \(AD = 10{\rm{ cm, }}AB = 8{\rm{ cm}}{\rm{.}}\)
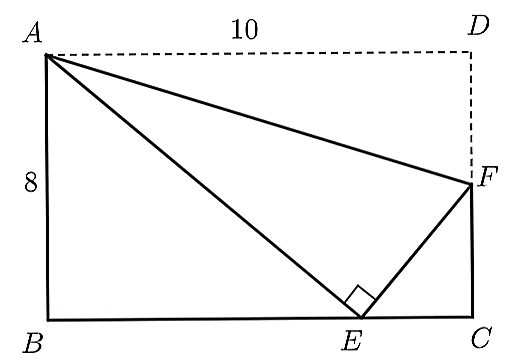
Hỏi độ dài của cạnh \(EC\) bằng bao nhiêu centimet?
Một bể kính hình hộp chữ nhật có hai cạnh đáy là \(60{\rm{ cm}}\) và \(30{\rm{ cm}}{\rm{.}}\) Trong bể có một khối đá hình chóp tam giác đều với diện tích đáy là \(270{\rm{ c}}{{\rm{m}}^2}\), chiều cao \(30{\rm{ cm}}{\rm{.}}\) Người ta đổ nước vào bể sao cho nước ngập khối đá và đo được mức nước là \(60{\rm{ cm}}{\rm{.}}\)
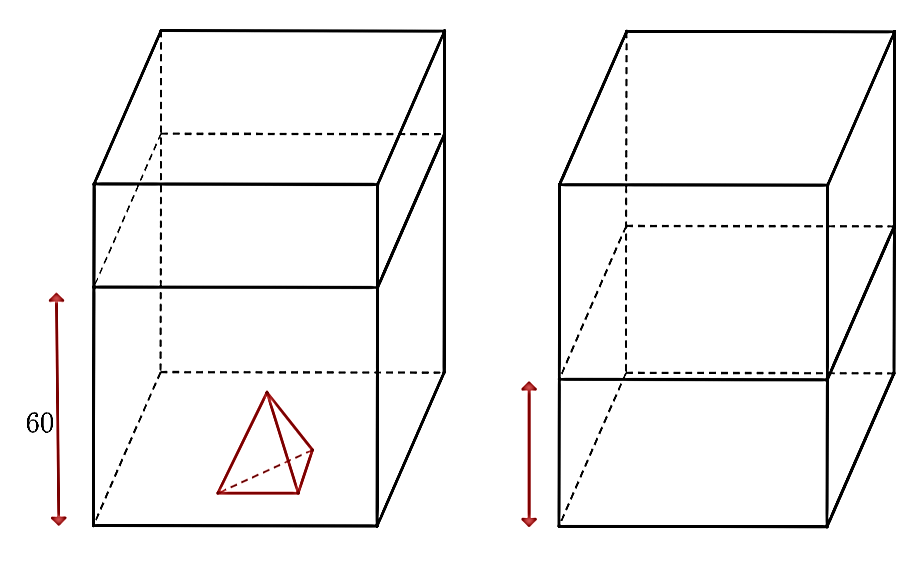
Khi lấy khối đá ra thì mực nước của bể cao bao nhiêu centimet?
B. TỰ LUẬN (3,0 điểm)
(1,0 điểm) Một số tự nhiên gồm hai chữ số có tổng bằng \[12.\] Nếu đổi chỗ hai chữ số đo cho nhau thì ta được một số mới bé hơn số ban đầu là 18 đơn vị. tìm số ban đầu.
a) Chứng minh rằng
b) Lấy điểm \(I\) thuộc đoạn \(AH\) (\(I\)không trùng với \[A,H\]). Qua \[B\] kẻ đường thẳng vuông góc với \[CI\] tại \[K\]. Chứng minh rằng \[CH.CB = CI.CK.\]
c) Tia \[BK\] cắt tia \[HA\] tại điểm \[D.\] Chứng minh \[CH.CB + DK.DB = C{D^2}.\]
(0,5 điểm) Tính giá trị lớn nhất của biểu thức








