Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 10)
29 câu hỏi
Phần 1. (3,0 điểm) Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Điều kiện xác định của phân thức \(\frac{{x - 5}}{{{x^2} - 4}}\) là
\(x \ne 4.\)
\(x \ne 2.\)
\(x \ne - 2.\)
\(x \ne 2;x \ne - 2.\)
Giá trị của phân thức \(\frac{{{x^2} - 1}}{{x - 2}}\) tại \(x = - 1\) là
\(0.\)
\(\frac{2}{3}.\)
\(\frac{{ - 2}}{3}.\)
\( - 1.\)
Phương trình nào là phương trình bậc nhất một ẩn trong các phương trình sau:
\(2x = 0.\)
\(3{x^2} + 1 = 0.\)
\(0x + 2 = 0.\)
\(\frac{1}{x} = 0.\)
Phương trình nào sau đây nhận \(x = 2\) là nghiệm?
\(3x + 6 = 0.\)
\(2x + 3 = 1 + x.\)
\(x + 2 = 4 + x.\)
\(2x - 4 = 0.\)
Trong các phát biểu sau phát biểu nào sai?
Đồ thị hàm số \(y = ax + b{\rm{ }}\left( {a \ne 0;b \ne 0} \right)\) là đường thẳng cắt đường thẳng \(y = ax{\rm{ }}\left( {a \ne 0} \right).\)
Đồ thị hàm số \(y = ax + b{\rm{ }}\left( {a \ne 0} \right)\) là đường thẳng song song với đường thẳng \(y = ax\) nếu \(b \ne 0\) và trùng với đường thẳng \(y = ax\) nếu \(b = 0.\)
Đồ thị hàm số \(y = ax + b{\rm{ }}\left( {a \ne 0;b \ne 0} \right)\) là đường thẳng cắt trục tung tại điểm có tung độ bằng \(b.\)
Đồ thị hàm số \(y = ax + b{\rm{ }}\left( {a \ne 0;b \ne 0} \right)\) là đường thẳng không đi qua gốc tọa độ.
Đường thẳng \(x = 2\) luôn cắt trục hoành tại điểm
Có hoành độ bằng \(2,\) tung độ bằng \(0.\)
Có hoành độ bằng \(0,\) tung độ bằng \(2.\)
Có hoành độ bằng \(2,\) tung độ bằng \(2.\)
Có hoành độ bằng \(2,\) tung độ tùy ý.
Gieo đồng thời hai con xúc xắc, số các kết quả có thể xảy ra là
\(10.\)
\(20.\)
\(12.\)
\(36.\)
Đội múa của trường gồm có 7 bạn nữ lớp 8A, 5 nam lớp 8A, 2 bạn nữ lớp 8B. Chọn ngẫu nhiên một bạn đội múa để múa chính. Số kết quả thuận lợi cho biến cố “Chọn được bạn nam” là
\(3.\)
\(7.\)
\(5.\)
\(4.\)
Nếu \(\Delta ABC\) và \(\Delta DEF\) có \(\widehat A = 50^\circ ,\widehat B = 60^\circ ,\widehat D = 50^\circ ,\widehat E = 70^\circ \) thì
\(\Delta ABC\) đồng dạng với \(\Delta DEF\) theo tỉ số \({k_1}\). \(\Delta DEF\) đồng dạng với \(\Delta GHK\) theo tỉ số \({k_2}\) thì \(\Delta ABC\) đồng dạng với \(\Delta GHK\) theo tỉ số
\(\frac{{{k_1}}}{{{k_2}}}.\)
\({k_1} + {k_2}.\)
\({k_1}.{k_2}.\)
\({k_1} - {k_2}.\)
Diện tích xung quanh của hình chóp tam giác đều là
Nửa chu vi đáy nhân với đường cao.
Chu vi đáy nhân với trung đoạn.
Nửa chu vi đáy nhân với trung đoạn.
Chu vi đáy nhân với chiều cao.
Thể tích của hình chóp tứ giác đều có diện tích mặt đáy bằng \(S,\) chiều cao tương ứng bằng \(h\) là
\(V = S.h.\)
\(V = \frac{S}{h}.\)
\(V = \frac{1}{2}S.h.\)
\(V = \frac{1}{3}S.h.\)
a) Với \(m = 0\) thì hai đường thẳng cắt nhau.
b) Với \(m = 2\) thì hai đường thẳng song song.
c) Khi \(m = 0\) thì hai đường thẳng cùng đi qua điểm \(M\left( {\frac{1}{2};3} \right).\)
d) Để hai đường thẳng cắt nhau tại một điểm thuộc trục hoành thì \(m = 6.\)
a) Các kết quả có thể xảy ra là \(10.\)
b) Có \(6\) kết quả thuận lợi cho biến cố “Học sinh được chọn là nữ”.
c) Xác suất của biến cố “Học sinh được chọn là nam” là \(0,6.\)
d) Xác suất của biến cố “Học sinh được chọn là nam và có tên bắt đầu bằng chữ H” là \(0,2.\)
Phần 3. (2,0 điểm) Câu hỏi trắc nghiệm trả lời ngắn
Trong các câu từ 15 đến 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Tìm giá trị của \(m\) để đường thẳng \(\left( {{d_1}} \right):y = \left( {2 - {m^2}} \right)x - m - 5\) song song với đường thẳng \(\left( {{d_2}:} \right)\)\(y = - 2x + 2m + 1\).
Gọi \(S\) là tập hợp các số tự nhiên có ba chữ số đôi một khác nhau được lập thành từ các số \(1,2,3,4,6\). Chọn ngẫu nhiên một số từ \(S\). Tính xác suất để số được chọn chia hết cho \(3.\)
(Kết quả ghi dưới dạng số thập phân)
Cho hình vẽ dưới đây. Biết \(AD \bot DC;DC \bot BC\) và độ dài các cạnh \(AB = 13{\rm{ cm, }}AC = 15{\rm{ cm,}}\) \(DC = 12{\rm{ cm}}{\rm{.}}\)
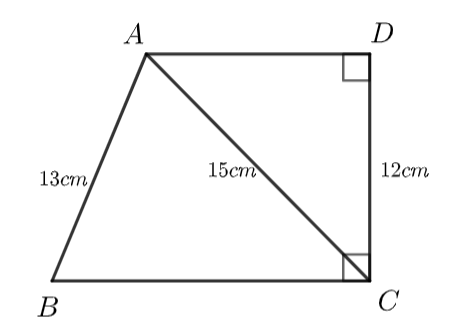
Hỏi độ dài đoạn thẳng \(BC\) bằng bao nhiêu centimet?
Một khối bê tông có dạng như hình dưới đây. Phần dưới của khối bê tông có dạng hình hộp chữ nhật, đáy là hình vuông có cạnh \(4{\rm{ dm,}}\) chiều cao \({\rm{2,5 dm}}{\rm{.}}\) Phần trên của khối bê tông có dạng hình chóp tứ giác đều, chiều cao \({\rm{10 dm}}{\rm{.}}\)
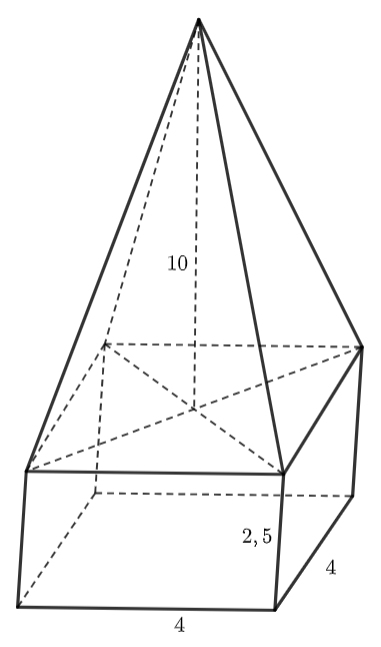
Tính thể tích của khối bê tông đó (đơn vị: dm3). (Kết quả làm tròn đến hàng phần mười)
B. TỰ LUẬN (3,0 điểm)
(1,0 điểm) Một tàu hỏa từ Hà Nội đi TP. Hồ Chí Minh. Sau 1 giờ 48 phút, một tàu hỏa khác khởi hành từ Nam Định cũng đi TP. Hồ Chí Minh với vận tốc nhỏ hơn vận tốc của tàu thứ nhất \(5{\rm{ km/h}}{\rm{.}}\) Hai tàu gặp nhau tại một nhà ga sau 4 giờ 48 phút kể từ khi tàu thứ nhất khởi hành. Tính vận tốc của mỗi tàu, biết rằng ga Nam Định nằm trên đường từ Hà Nội đi TP. Hồ Chí Minh và cách ga Hà Nội \(87{\rm{ km}}{\rm{.}}\)
a) Chứng minh và
b) Chứng minh rằng \(A{H^2} = BH.CH.\)
c) Gọi \(M\) và \(N\) lần lượt là trung điểm của \(AB\) và \(BC.\) Chứng minh: \(\frac{1}{4}CH.CB = M{N^2}.\)
(0,5 điểm) Tính giá trị nhỏ nhất của biểu thức .








