Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 8)
29 câu hỏi
Phần 1. (3,0 điểm) Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Biểu thức nào sau đây không phải là phân thức đại số?
\(\frac{{2x + 1}}{{x - 3}}.\)
\(\frac{{\sqrt x }}{{x - 3}}.\)
\(\frac{{\sqrt {2x} + 1}}{{x - 3}}.\)
\(\frac{{2x + 1}}{{\sqrt {x - 3} }}.\)
Phân thức \(\frac{{2y}}{{3x}}\) bằng phân thức nào trong các phân thức sau?
\(\frac{{4y}}{{6x}}.\)
\(\frac{{4y}}{{3x}}.\)
\(\frac{{2y}}{{6x}}.\)
\(\frac{y}{{3x}}.\)
Phương trình nào sau đây không là phương trình bậc nhất một ẩn?
\(2x - 2023 = 0.\)
\(3x = 0.\)
\(2x + \sqrt 3 = 0.\)
\(\left( {x - 2} \right)\left( {x + 2} \right) = 0.\)
\(x = - 2\) là nghiệm của phương trình:
\(2x - 4 = 0.\)
\(2x + 4 = 0.\)
\(2x - 2 = 0.\)
\(2x + 2 = 0.\)
Trong các hàm số sau, hàm số bậc nhất là
\(y = 2x - 3.\)
\(y = \frac{3}{x}.\)
\(y = 2{x^2} - 2.\)
\({y^2} = x - 3.\)
Đường thẳng \(y = 1\) luôn cắt trục tung tại điểm
Có tung độ bằng \(1,\) hoành độ bằng \(0.\)
Có hoành độ bằng \(1,\) tung độ bằng \(0.\)
Có hoành độ bằng \(1,\) tung độ bằng \(1.\)
Có tung độ bằng \(1,\) hoành độ tùy ý.
Đội văn nghệ khối 8 của một trường có 3 học sinh nam lớp 8A, 3 học sinh nữ lớp 8B, 1 học sinh nam lớp 8C và 2 học sinh nữ lớp 8C. Chọn ngẫu nhiên một học sinh trong đội văn nghệ khối 8 để tham gia chương trình văn nghệ của trường. Số kết quả có thể xảy ra là:
\(6.\)
\(7.\)
\(8.\)
\(9.\)
Một chiếc hộp đựng \(15\) chiếc bút gồm \(5\) bút đỏ, \(1\) bút xanh, \(6\) bút tím và \(3\) bút đen. Bạn An lấy ngẫu nhiên một chiếc bút trong hộp. Biến cố: “An lấy được chiếc bút màu xanh” là biến cố:
không thể xảy ra.
chắc chắn xảy ra.
có 1 kết quả thuận lợi.
có 5 kết quả thuận lợi.
Chọn khẳng định đúng.
Hai tam giác đồng dạng thì bằng nhau.
Hai tam giác bằng nhau thì đồng dạng.
Hai tam giác cân luôn đồng dạng.
Hai tam giác vuông luôn đồng dạng.
Cho , hãy chọn đáp án đúng.
\(\widehat M = \widehat R.\)
\(\frac{{MN}}{{QR}} = \frac{{NP}}{{QS}}.\)
\(\frac{{MN}}{{QR}} = \frac{{NP}}{{RS}}.\)
\(\widehat N = \widehat Q.\)
Diện tích xung quanh của hình chóp tứ giác đều là \({S_{xq}} = p.d\). Trong đó \(d\) là gì?
Chiều cao.
Trung đoạn.
Nửa chu vi đáy.
Cạnh đáy.
Các mặt bên của hình chóp tam giác đều là hình gì?
Tam giác đều.
Tam giác nhọn.
Tam giác cân.
Tam giác vuông.
a) Hai đường thẳng \(\left( {{d_1}} \right),\left( {{d_2}} \right)\) cắt nhau.
b) Hai đường thẳng \(\left( {{d_1}} \right),\left( {{d_2}} \right)\) cùng đi qua điểm \(A\left( {1;0} \right).\)
c) Đường thẳng \(\left( {{d_3}} \right)\) đi qua \(E\left( { - 1;0} \right)\) và song song với \(\left( {{d_1}} \right)\) là \(y = 2x - 1.\)
d) Đường thẳng \(\left( {{d_4}} \right)\) đi qua \(A\), cắt đường thẳng \(\left( {{d_2}} \right)\) và có hệ số góc là \(3\) là đường thẳng \(y = 3x + 1.\)
a) Có \(20\) kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là số lẻ”.
b) Có \(5\) kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là bình phương của một số”.
c) Xác suất của biến cố “Số xuất hiện trên thẻ được rút ra là bình phương của một số” là \(0,125.\)
d) Xác suất của biến cố “Số xuất hiện trên thẻ được rút ra là lập phương của một số” là \[0,075.\]
Phần 3. (2,0 điểm) Câu hỏi trắc nghiệm trả lời ngắn
Trong các câu từ 15 đến 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Xác định hệ số góc của đường thẳng đi qua hai điểm \(A\left( { - 4;0} \right)\) và \(B\left( {0;5} \right)\).
(Kết quả ghi dưới dạng số thập phân)
Có hai túi I và II mỗi túi chứa 5 tấm thẻ được đánh số \(1;2;3;4;5\). Rút ngẫu nhiên từ mỗi túi ra một tấm thẻ và nhân hai số ghi trên tấm thẻ với nhau. Tính xác suất của biến cố \(A\): “Kết quả là \(1\) hoặc một số nguyên tố”. (Kết quả ghi dưới dạng số thập phân)
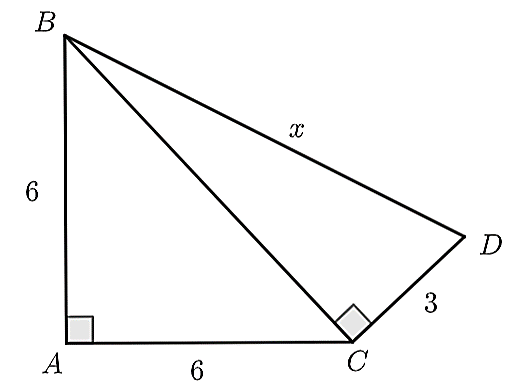
Tìm giá trị của \(x\) trong hình vẽ sau:
Nhà bạn thu có một đèn trang trí có dạng hình chóp tam giác đều như hình bẽ bên. Các cạnh của hình chóp đều bằng nhau và bằng \(20{\rm{ cm}}\). Bạn Thu dự định sẽ dán các mặt bên của đèn bằng những tấm giấy màu.
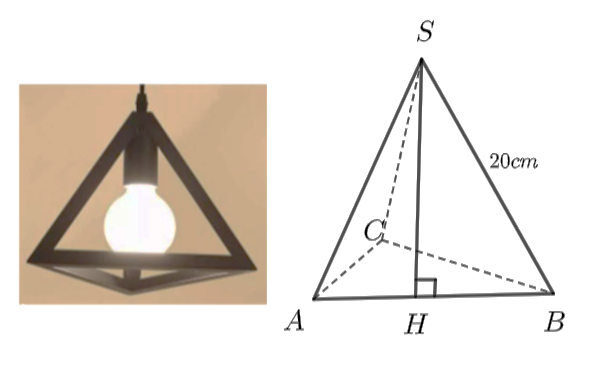
Tính diện tích giấy màu mà bạn Thu sử dụng (đơn vị: cm2, coi như mép dán không đáng kể). Cho biết \(\sqrt {300} = 17,32\). (Kết quả làm tròn đến hàng đơn vị)
B. TỰ LUẬN (3,0 điểm)
(1,0 điểm) Cô Hương đầu tư \(400\) triệu đồng vào hai khoản: mua trái phiếu doanh nghiệp với lãi suất \(8\% \) một năm và mua trái phiếu chính phủ với lãi suất \(6\% \) một năm. Cuối năm cô Hương nhận được \(29\) triệu đồng tiền lãi. Hỏi cô Hương đã đầu tư vào mỗi khoản bao nhiêu tiền?
a) Chứng minh rằng .
b) Chứng minh rằng \(B{C^2} = BD.DH.\)
c) Kẻ \(DE\) là đường phân giác của tam giác \(ABD\). Gọi \(I\) là giao điểm của \(DE\) và \(AH\). Chứng minh \(\Delta AIE\) cân và \(A{E^2} = IH.EB.\)
(0,5 điểm) Rút gọn biểu thức:








