Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 5)

b) Rút gọn biểu thức \(K.\)

c) Tìm giá trị nguyên của \(x\) để biểu thức \(K\) nhận giá trị nguyên.

Hàm chi phí đơn giản nhất là hàm chi phí bậc nhất \(y = ax + b,\) trong đó \(b\) biểu thị chi phí cố định của hoạt động kinh doanh và hệ số \(a\) biểu thị chi phí của mỗi mặt hàng được sản xuất. Giả sử rằng một xưởng sản xuất xe đạp có chi phí cố định hằng ngày là 36 triệu đồng và mỗi chiếc xe đạp có chi phí sản xuất là \(1,8\) triệu đồng.

a) Viết công thức của hàm số bậc nhất biểu thị chi phí \(y\) (triệu đồng) để sản xuất \(x\) (xe đạp) trong một ngày.

b) Có thể sản xuất bao nhiêu chiếc xe đạp trong ngày, nếu chi phí trong ngày đó là 72 triệu đồng?

Tại điểm tiêm phòng Covid-19 trường A, một bàn tiêm dự định tiêm một số mũi tiêm vaccine phòng Covid-19 cho người dân trong 20 ngày. Do yêu cầu cấp bách của việc phòng bệnh, bàn tiêm đã tăng năng suất thêm 20% nên sau 18 ngày không những đã tiêm xong số mũi tiêm dự định mà còn tiêm thêm được 24 mũi tiêm nữa. Tính số mũi tiêm phòng Covid-19 mà một bàn tiêm dự định tiêm.

a) Gọi \(K\) là tập hợp gồm các kết quả có thể xảy ra đối với thành viên được chọn. Tính số phần tử của tập hợp \(K\).

b) Tính xác suất của mỗi biến cố: “Thành viên được chọn ra đến từ vùng Tây Nguyên”.

c) Tính xác suất của mỗi biến cố:“Thành viên được chọn ra đến từ vùng Đông Nam Bộ”.

a) Chứng minh: $\mathrm{\Delta ABD}\backsim \mathrm{\Delta ACE}$

b) Chứng minh: \(\widehat {ABC} + \widehat {EDC} = 180^\circ \).

c) Gọi \[M,{\rm{ }}N\] lần lượt là trung điểm của đoạn thẳng \[BD\] và \[CE.\] Vẽ \[AK\] là phân giác của \[\widehat {MAN}\,\,(K \in BC).\] Chứng minh \[KB \cdot AC = KC \cdot AB.\]

Để xác định chiếc điện thoại là bao nhiêu inch, các nhà sản xuất đã dựa vào độ dài đường chéo của màn hình điện thoại, biết \(1\,\,{\rm{inch}} \approx 2,54\,\,{\rm{cm}}\), điện thoại có chiều rộng là \[7\,\,{\rm{cm;}}\] chiều dài là \[15,5{\rm{ cm}}.\] Hỏi chiếc điện thoại theo hình vẽ là bao nhiêu inch? (Làm tròn kết quả đến hàng đơn vị).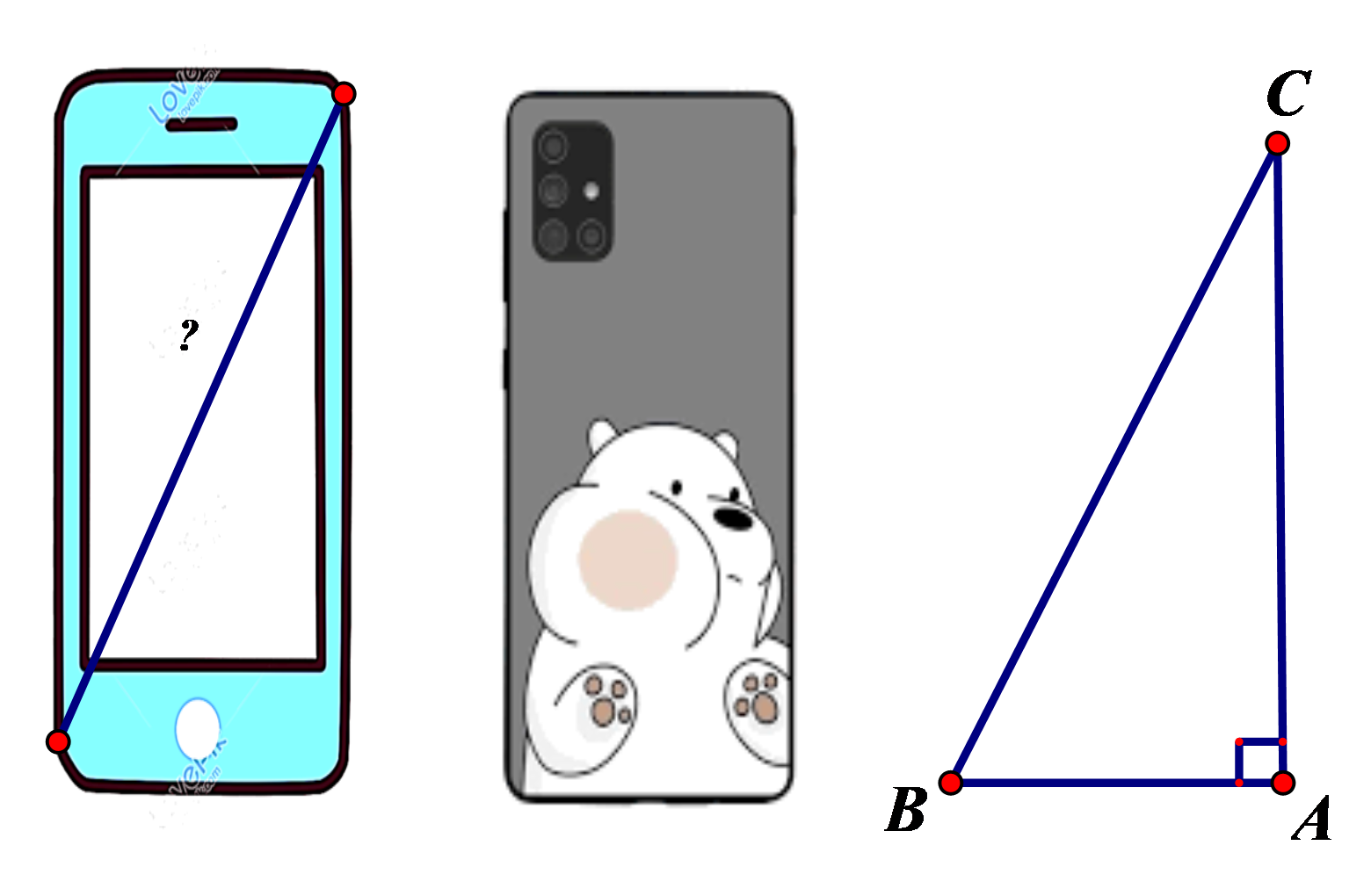

Tính diện tích xung quanh của hình chóp tứ giác đều được gấp từ miếng bìa có kích thước như hình bên.

(0,5 điểm)Trên 6 chiếc thẻ, mỗi thẻ đánh một trong các số trong tập hợp \[\left\{ { - 2\,;\,\, - 1\,;\,\,0\,;\,\,3\,;\,\,4\,;\,\,5} \right\}\] (không có có thẻ nào có số trùng nhau). Hai thẻ được chọn ngẫu nhiên từ tập hợp trênvà đem nhân với nhau. Hỏi xác suất để tích hai số trên hai tấm bằng 0 là bao nhiêu?