Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 12)
29 câu hỏi
Phần 1. (3,0 điểm) Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Trong các biểu thức sau, biểu thức nào không là phân thức đại số?
\(\frac{{\sqrt x }}{{x - 3}}.\)
\(\frac{{2x + 1}}{{x - 3}}.\)
\(\frac{{2x - 1}}{{x - 3}}.\)
\(\frac{x}{{x - 3}}.\)
Phân thức \(\frac{{2xy}}{{3{x^2}y}}\) bằng phân thức nào trong các phân thức sau?
\(\frac{{2y}}{{3x}}.\)
\(\frac{{2y}}{{5x}}.\)
\(\frac{{3y}}{{2x}}.\)
\(\frac{2}{{3x}}.\)
Gọi \(x\) (km) là chiều dài quãng đường \(AB\). Biểu thức biểu thị vận tốc một xe đạp đi từ \(A\) đến \(B\) trong \(5\) giờ là
\(\frac{x}{5}.\)
\(5x.\)
\(5 + x.\)
\(5 - x.\)
Phương trình nào sau đây có nghiệm là \(x = 2\)?
\(2x + 1 = 5x.\)
\(2x - 4 = 3x - 9.\)
\(x - 3 = 2x - 5.\)
\(2x - 8 = 3.\)
Hàm số nào sau đây là hàm số bậc nhất?
\(y = 0x + 3.\)
\(y = - 2x - 5.\)
\(y = - {x^2} + 1.\)
\(y = \frac{1}{x} + 3.\)
Đường thẳng \(y = - 3 - 2x\) có hệ số góc là
\(3.\)
\(2.\)
\( - 2.\)
\( - 3.\)
Gieo một con xúc xắc cân đối đồng chất. Gọi \(A\) là biến cố “Gieo được mặt có số chấm là số lẻ”. Số kết quả thuận lợi là
\(1.\)
\(2.\)
\(3.\)
\(5.\)
Gieo một con xúc xắc cân đối đồng chất. Gọi \(B\) là biến cố: “Gieo được mặt có số chấm là số chẵn”. Xác suất của biến cố \(B\) là
\(\frac{1}{2}.\)
\(\frac{1}{6}.\)
\(\frac{1}{3}.\)
\(\frac{2}{3}.\)
Cho \(\Delta RSK\) và \(\Delta PQM\) có \(\frac{{RS}}{{PQ}} = \frac{{RK}}{{PM}} = \frac{{SK}}{{QM}}\), khi đó, ta có:
Nếu theo tỉ số thì theo tỉ số là
\(\frac{1}{4}.\)
\(\frac{1}{2}.\)
\(2.\)
\(4.\)
Cho các miếng bìa sau.
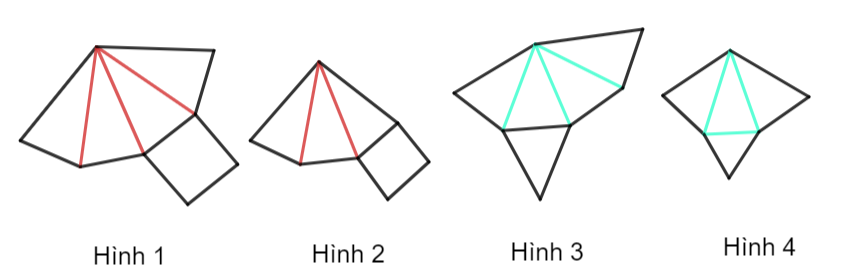
Miếng bìa nào sau khi gấp và dán lại thì được một hình chóp tứ giác đều?
Hình 1.
Hình 2.
Hình 3.
Hình 4.
Đường cao của hình chóp tam giác đều là
Đoạn thẳng nối đỉnh của hình chóp và trọng tâm của tam giác đáy.
Đoạn thẳng nối đỉnh của hình chóp và trung điểm của một cạnh đáy.
Đoạn thẳng nối đỉnh của hình chóp và một điểm tùy ý nằm trong mặt đáy.
Đoạn thẳng nối đỉnh của hình chóp và một điểm bất kì trên cạnh bên của hình chóp.
a) Với \(m \ne 1\) thì đường thẳng \(\left( d \right)\) cắt \(\left( {d'} \right):y = 2mx + 8.\)
b) Đường thẳng \(\left( d \right)\) đi qua điểm \(A\left( {0;5} \right)\) khi \(m = 3.\)
c) Với \(m = 5\) thì đường thẳng \(\left( d \right)\) song song với đường thẳng \(y = 2x - 1.\)
d) Để \(\left( d \right)\) cắt đường thẳng \(y = - x + 9\) tại điểm có tung độ là \(5\) thì \(m = \frac{{12}}{5}.\)
a) Có \(21\) kết quả thuận lợi cho biến cố “Chiếc bút lấy ra là bút mực xanh”.
b) Có \(3\) kết quả thuận lợi cho biến cố “Chiếc bút lấy ra là bút được ghi số tròn chục”.
c) Xác suất của biến cố “Chiếc bút được lấy ra là bút mực đỏ” là \(0,3.\)
d) Xác suất của biến cố “Chiếc bút được lấy ra là bút mực xanh và ghi số chia hết cho 3” là \(\frac{2}{{15}}.\)
Phần 3. (2,0 điểm) Câu hỏi trắc nghiệm trả lời ngắn
Trong các câu từ 15 đến 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Cho đường thẳng \(\left( d \right):y = \left( {m - 1} \right)x - 3\) và \(\left( {d'} \right):y = 2x - \left( {m - 1} \right)\). Có bao nhiêu giá trị của \(m\) để hai đường thẳng \(\left( d \right)\) và \(\left( {d'} \right)\) trùng nhau?
Một hộp có \(50\) chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số sau \(1;2;3;4,....;49;50,\) hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của biến cố “Số trên thẻ được rút ra là vừa là bình phương của một số và vừa chia hết cho \(3\)”.
(Kết quả ghi dưới dạng số thập phân)
Trong tam giác vuông dưới đây, có \(BC = 3{\rm{ cm; }}CD = 2{\rm{ cm; }}AC = n;AD = m.\)
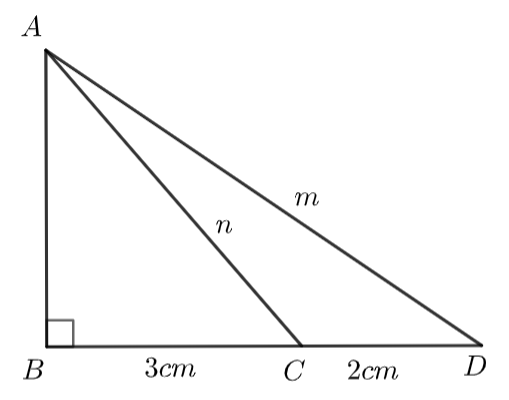
Tính giá trị của \({m^2} - {n^2}.\)
Đỉnh Fansipan (Lào Cai) cao \(3143{\rm{ m,}}\) là đỉnh núi cao nhất Đông Dương. Trên đỉnh núi, người ta đặt một chóp làm bằng inox có dạng hình chóp tam giác đều dài \(60{\rm{ cm,}}\)chiều cao \(90{\rm{ cm}}\) (như hình).
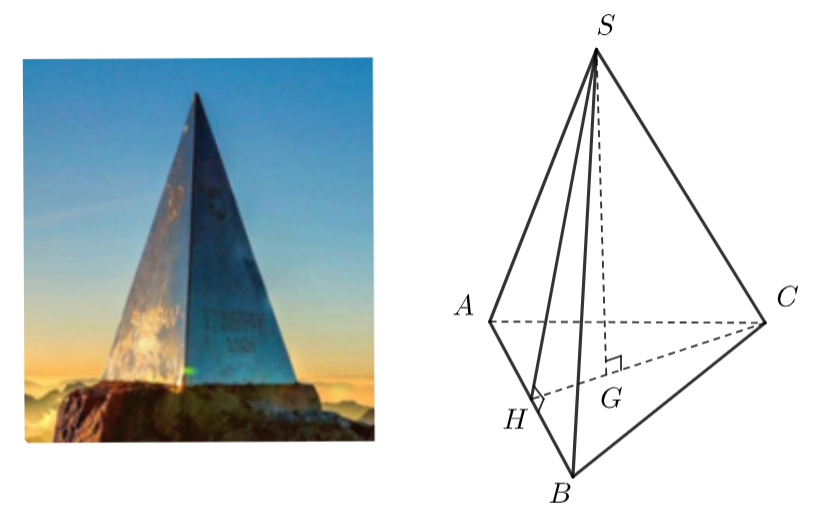
Hỏi tổng diện tích các mặt bên của hình chóp bằng bao nhiêu? (đơn vị: cm2)
(Kết quả làm tròn đến hàng đơn vị)
B. TỰ LUẬN (3,0 điểm)
(1,0 điểm) Một hợp tác xã thu hoạch thóc, dự định thu hoạch \(20\) tấn thóc mỗi ngày, nhưng khi thu hoạch đã vượt mức \(6\) tấn mỗi ngày nên không những đã hoàn thành kế hoạch sớm một ngày mà còn thu hoạch vượt mức \(10\) tấn. Tính số tấn thóc đã dự định thu hoạch.
a) Chứng minh \(AE.AB = A{D^2} = AF.AC\) và \(\widehat {AFE} = \widehat {ABC}\).
b) Gọi \(I\) là giao điểm của \(FE\) và tia \(CB\). Chứng minh \(I{D^2} = IE.IF\).
c) Gọi \(H\) là trực tâm của \(\Delta ABC,\) tia \(HB\) cắt \(EF\) tại \(K.\) Chứng minh \(DK \bot BH.\)
(0,5 điểm) Cho \(a,b\) là các số thực không âm thỏa mãn \({a^2} + {b^2} = 1\). Đặt \(P = \frac{{2ab}}{{a + b + 1}}\). Chứng minh rằng: \({\left( {P + 1} \right)^2} \le 2\).








