Bộ 5 đề thi giữa kì 1 Toán 9 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 5
21 câu hỏi
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn (3,0 điểm)
Mẫu thức chung của phương trình \[\frac{1}{{x - 1}} + \frac{3}{{x + 1}} = 0\] là
\(x\left( {x - 1} \right)\left( {x + 1} \right)\).
\({\left( {x - 1} \right)^2}.\)
\({\left( {x + 1} \right)^2}\).
\(\left( {x - 1} \right)\left( {x + 1} \right).\)
Phương trình \[2x\left( {3x - 1} \right) + 6x - 2 = 0\] có nghiệm là
\[x = \frac{1}{3}.\]
\[x = \frac{1}{3}\] và \[x = - 1\].
\[x = - 1\].
\(x = 1\) và \(x = - \frac{1}{3}.\)
Phương trình nào sau đây là phương trình bậc nhất hai ẩn?
\[2{x^2} + 2 = 0.\]
\[3y - 1 = 5y\left( {y - 2} \right).\]
\(2x + \frac{y}{2} - 1 = 0.\)
\[\frac{3}{x} + y = 0.\]
Phương trình nào dưới đây nhận cặp số \(\left( { - 2;\,\,4} \right)\) làm nghiệm?
\[x - 2y = 0.\]
\[2x + y = 0.\]
\[x - y = 2.\]
\[x + 2y + 1 = 0.\]
Cặp số nào sau đây là nghiệm của hệ phương trình \[\left\{ \begin{array}{l}3x + 4y = 42\\10x - 9y = 6\end{array} \right.?\]
\[\left( {6;\,\, - 6} \right)\].
\[\left( {6;\,\,6} \right)\].
\[\left( { - \frac{{354}}{{13}};\,\,\frac{{402}}{{13}}} \right)\].
\[\left( {\frac{{354}}{{13}};\,\,\frac{{402}}{{13}}} \right)\].
Hình nào dưới đây biểu diễn tất cả các nghiệm của phương trình \[2x-3y = 5?\]
A. 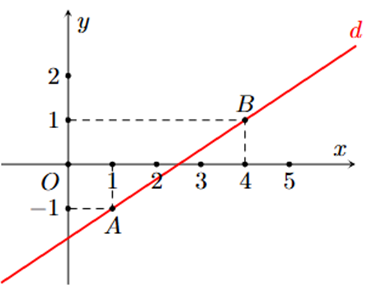
B. 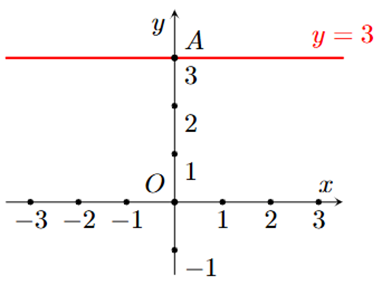
C. 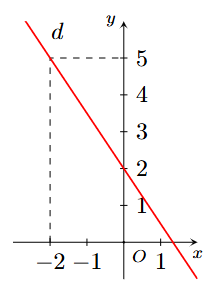
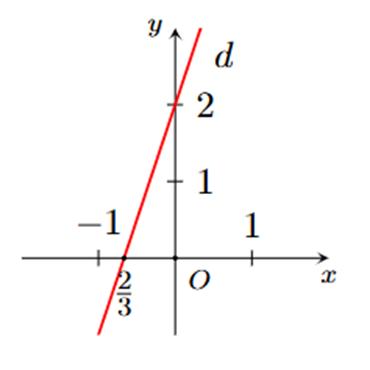
Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn?
\[x + y > 8\].
\[0x + 5 \ge 0\].
\[2x-3 > 4\;\].
\[{x^2} - 6x + 1 \le 0.\]
Biển báo giao thông trong hình bên báo đường cấm các xe cơ giới và thô sơ (kể cả các xe được ưu tiên theo quy định) có độ dài toàn bộ kể cả xe và hàng lớn hơn trị số ghi trên biển đi qua. Nếu xe có chiều rộng lớn hơn \[3,2\,\,{\rm{m}}\] thì không được phép lưu thông để đảm bảo an toàn cho cả xe và các phương tiện khác, cũng như tránh gây cản trở giao thông. Nếu một xe tải đi trên đường đó có chiều rộng \(a\,\,(m)\) thỏa mãn điều kiện nào sau đây là đúng nhất?

\[a \le 3,2.\]
\[a > 3,2.\]
\[a \ge 3,2.\]
\[a = 3,2.\]
Cho tam giác \(MNP\) vuông tại \(M\) có đường cao \(MH\) và \(\widehat P = \alpha \). Tỉ số \(\frac{{PH}}{{MP}}\) bằng
\(\cot \alpha \).
\[\cos \alpha \].
\(\sin \alpha \).
\(\tan \alpha .\)
Tam giác \[ABC\] vuông tại \[A\]. Khẳng định nào sau đây đúng?
\[AC = AB.\tan B.\]
\[AB = BC.\tan B.\]
\[AC = BC.\tan B.\]
\[AB = AC.\tan B.\]
Cho góc \(\alpha \) thỏa mãn \(0^\circ < \alpha < 90^\circ \). Biết \(\sin \alpha = \frac{3}{5}\). Giá trị của \(\cos \left( {90^\circ - \alpha } \right)\) bằng
\(\frac{5}{4}\).
\(\frac{4}{5}\).
\(\frac{5}{3}\).
\(\frac{3}{5}\).
Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = 10\), \(AC = 6\). Tỉ số lượng giác \(\tan C\) có kết quả gần nhất với giá trị nào dưới đây?
\(1,33.\)
\(0,88.\)
\(0,68.\)
\(0,75.\)
Phần 2. Câu trắc nghiệm đúng sai (2,0 điểm)
Cho phương trình \[2x - 5y = 1{\rm{ }}\left( * \right)\].
a) Cặp số \[\left( { - 2\,;\,\,1} \right)\] là nghiệm của phương trình \[\left( * \right)\].
b) Phương trình \[\left( * \right)\] là phương trình bậc nhất hai ẩn có vô số nghiệm.
c) Hệ số \[a;\,\,b;\,\,c\] của phương trình \[\left( * \right)\] lần lượt là \[2\,;\,\, - 5\,;\,\,1.\]
d) Tập hợp các điểm có tọa độ \(\left( {x\,;\,\,y} \right)\) thỏa mãn phương trình \[\left( * \right)\] là đường thẳng \[y = 2x - 1.\]
Cho ba số \(a,\,\,b,\,\,c\) và \(a \le b.\)
a) \(a + c \le b + c.\) b) \(ac \ge bc\) với \(c > 0.\)
c) \( - \frac{a}{c} \ge - \frac{b}{c}\) với \(c < 0.\) d) \({a^2} \le {b^2}.\)
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn (2,0 điểm)
Phương trình \(\frac{{x + 2}}{{x - 2}} - \frac{{x - 2}}{{2 + x}} = \frac{{{x^2} + 16}}{{{x^2} - 4}}\) có nghiệm là bao nhiêu?
Gọi \(\left( {x;\,\,y} \right)\) là nghiệm của hệ phương trình \[\left\{ \begin{array}{l}2\left( {x + y} \right) + 3\left( {x - y} \right) = 4\\\left( {x + y} \right) + 2\left( {x - y} \right) = 5\end{array} \right..\] Bạn An sau khi giải hệ phương trình thì viết được hệ thức \(y = ax.\) Tìm \(a.\)
Tìm giá trị nhỏ nhất của \(x\) thỏa mãn bất phương trình \(1 + \frac{{x + 4}}{5} \le x - \frac{{x + 3}}{3}\).
Cho tam giác \[ABC\] vuông tại \[C\] có \[BC = 1,2\,\,{\rm{cm}}\,{\rm{, }}AC = 0,9\,\,{\rm{cm}}.\] Tính \[\sin B + \cos B.\]
B. TỰ LUẬN (3,0 điểm)
(1,0 điểm)Giải bài toán sau bằng cách lập hệ phương trình:
Gen B có \(3\,\,600\) liên kết hydrogen và có hiệu giữa nucleotide loại \[T\] với loại nucleotide không bổ sung với nó là \(300\) nucleotide. Tính số nucleotide từng loại của gen B. Biết rằng, để tính số lượng nucleotide \[\left( {A,{\rm{ }}T,{\rm{ }}G,{\rm{ }}C} \right)\] trong phân tử DNA, ta áp dụng nguyên tắc bổ sung: “\[A\] liên kết với \[T\] bằng 2 liên kết hydrogen và \[G\] liên kết với \[C\] bằng 3 liên kết hydrogen” và \(\% A = \% T,\,\,\% G = \% C.\) Tổng số nucleotide trong gen:
\(N = A + T + G + C = 2A + 2G = 2T + 2C.\)
(1,5 điểm)
1) Cho tam giác \(ABC\) có \(BC = 16\,{\rm{cm}},\,\,\widehat {ABC} = 45^\circ ,\,\,\widehat {ACB} = 30^\circ .\) Gọi \(N\) là chân đường vuông góc kẻ từ \(A\) đến cạnh \(BC.\) Tính độ dài cạnh \(AN\) (làm tròn kết quả đến chữ số thập phân thứ hai).
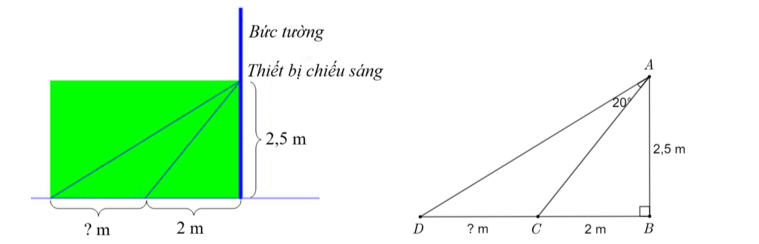
2) Người ta cần lắp đặt một thiết bị chiếu sáng gắn trên tường cho một phòng triển lãm như hình vẽ. Thiết bị này có góc chiếu sáng là \(20^\circ \) và cần đặt cao hơn mặt đất là \(2,5\,\,{\rm{m}}.\) Người ta đặt thiết bị chiếu sáng này sát tường và được canh chỉnh sao cho trên mặt đất dải ánh sáng bắt đầu từ vị trí cách tường \(2\,\,{\rm{m}}\) (như hình vẽ). Tính độ dài vùng được chiếu sáng trên mặt đất (làm tròn kết quả đến chữ số thập phân thứ nhất).
(0,5 điểm) Một công ty du lịch tổ chức một chuyến đi tham quan. Giá vé cho 80 khách đầu tiên là \[5\,\,000\,\,000\] đồng/người. Nếu có nhiều hơn 40 người đăng ký, mỗi khi có thêm 1 người, giá vé sẽ giảm \[50\,\,000\] đồng/người cho toàn bộ hành khách. Tính số lượng khách tối ưu để công ty đạt doanh thu cao nhất.








