Bộ 5 đề thi cuối kì 1 Toán 9 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 4
21 câu hỏi
Phần 1. (3,0 điểm) Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Điều kiện xác định của phương trình \(\frac{{4x - 1}}{{x - 4}} + 1 = \frac{3}{{x + 2}}\) là
\(x \ne 2.\)
\(x \ne 3.\)
\(x \ne - 2;{\rm{ }}x \ne 3.\)
\(x \ne - 3;{\rm{ }}x \ne 2.\)
Phương trình nào dưới đây có tập xác định là \(x \ne - 1\) và \(x \ne 3\)?
\(\frac{2}{{x + 1}} = \frac{3}{{x + 3}}.\)
\(\frac{5}{{x - 1}} = \frac{2}{{x - 3}}.\)
\(\frac{{x + 3}}{{x - 1}} = 2.\)
\(\frac{2}{{x + 1}} = \frac{3}{{x - 3}}.\)
Phương trình nào dưới đây là phương trình bậc nhất hai ẩn \(x\) và \(y\)?
\(5x + y = 7.\)
\(2{x^2} + y = 4.\)
\(0x + 0y = - 2.\)
\(2{x^2} + 2{y^2} = 3.\)
Trong các hệ phương trình dưới đây, hệ phương trình nào là hệ phương trình bậc nhất hai ẩn?
\(\left\{ \begin{array}{l}x + y = 1\\2x - y = - 1\end{array} \right..\)
\(\left\{ \begin{array}{l}x + 2{y^2} = 4\\x + y = 0\end{array} \right..\)
\(\left\{ \begin{array}{l}x + 2y = 4\\3{x^2} - 2y = 0\end{array} \right..\)
\(\left\{ \begin{array}{l}{x^2} + 2{y^2} = 4\\3x - y = 0\end{array} \right..\)
Bất phương trình nào dưới đây là bất phương trình bậc nhất một ẩn?
\(x + 2y > 0.\)
\(\frac{1}{x} - 3 > 0.\)
\({x^2} + 1 > 0.\)
\(\frac{x}{2} + 1 > 0.\)
Cho \(a > b\). Khẳng định nào dưới đây là đúng?
\(a - 3 > b - 3.\)
\( - 3a + 4 > - 3b + 4.\)
\(2a + 3 < 2b + 3.\)
\( - 5b - 1 < - 5a - 1.\)
Điều kiện xác định của căn thức \(\sqrt {2x + 3} \) là
\(x \ge \frac{{ - 3}}{2}.\)
\(x \le \frac{{ - 3}}{2}.\)
\(x \ge \frac{{ - 2}}{3}.\)
\(x \le \frac{{ - 2}}{3}.\)
Với mọi số \(a\), ta luôn có:
\(\sqrt {{a^2}} = a.\)
\(\sqrt {{a^2}} = \left| a \right|.\)
\(\sqrt a = \left| a \right|.\)
\(\sqrt {{a^2}} = - a.\)
Cho tam giác vuông có \(\alpha \) là góc nhọn. Khẳng định nào sau đây là sai?
Tỉ số giữa cạnh huyền và cạnh kề được gọi là cosin của góc \(\alpha \), kí hiệu \(\sin \alpha .\)
Tỉ số giữa cạnh kề và cạnh huyền được gọi là cosin của góc \(\alpha \), kí hiệu \(\cos \alpha .\)
Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc \(\alpha \), kí hiệu \(\tan \alpha .\)
Tỉ số giữa cạnh kề và cạnh đối được gọi là tang của góc \(\alpha \), kí hiệu \(\cot \alpha .\)
Nếu \(\alpha \) là góc nhọn thì \[\sin \left( {90^\circ - \alpha } \right)\] bằng
\(\sin \alpha .\)
\(\tan \alpha .\)
\(\cos \alpha .\)
\(\cot \alpha .\)
Cho hai đường tròn đồng tâm \(O\) có bán kính lần lượt là \(R\) và \(r{\rm{ }}\left( {R > r} \right).\) Diện tích phần nằm giữa hai đường tròn này – hình vành khăn được tính
\(S = \pi \left( {{r^2} - {R^2}} \right).\)
\(S = \pi \left( {{r^2} + {R^2}} \right).\)
\(S = \pi \left( {{R^2} - {r^2}} \right).\)
Kết quả khác.
Đường thẳng \(d\) cách tâm \(O\) của đường tròn \(\left( {O;\,\,4{\rm{ cm}}} \right)\) một khoảng \({\rm{3 cm}}.\) Khi đó vị trí tương đối của \(d\) và đường tròn \(\left( {O;\,\,4{\rm{ cm}}} \right)\) là
Cắt nhau.
Không giao nhau.
Tiếp xúc nhau.
Không kết luận được.
Phần 2. (2,0 điểm) Câu trắc nghiệm đúng sai
Trong câu 13, 14, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
rong cuộc thi “Đố vui để học”, mỗi thí sinh phải trả lời 12 câu hỏi của ban tổ chức. Mỗi câu hỏi gồm bốn phương án, trong đó chỉ có một phương án đúng. Với mỗi câu hỏi, nếu trả lời đúng thì được cộng 5 điểm, trả lời sai bị trừ 2 điểm. Khi bắt đầu cuộc thi mỗi thí sinh có sẵn 20 điểm. Thí sinh nào đạt từ 50 điểm trở lên sẽ được vào vòng tiếp theo. Gọi \(x\) là số câu trả lời đúng \(\left( {0 \le x \le 12,x \in \mathbb{N}} \right)\).
a) Số câu trả lời sai là \(12 - x\) câu.
b) Tổng số điểm đạt được khi trả lời hết 12 câu hỏi là: \(2 + 5x - 2\left( {12 - x} \right)\) điểm.
c) Để vào vòng tiếp theo thì thí sinh cần đạt điểm thỏa mãn \(20 + 5x - 2\left( {12 - x} \right) > 50\) điểm.
d) Thí sinh muốn vào vòng tiếp theo cần trả lời đúng ít nhất 9 câu.
Hai người A và B đứng cùng bờ sông nhìn ra một cồn C nổi giữa sông. Người A nhìn ra cồn với một góc \(43^\circ \) so với bờ sông, người B nhìn ra cồn với một góc \(28^\circ \) so với bờ sông. Hai người đứng cách nhau \(250{\rm{ m}}\) như hình minh họa dưới đây. (Kết quả làm tròn đến hàng phần trăm)
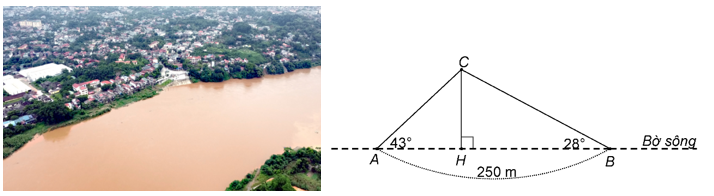
a)\(CH = AH \cdot \tan 43^\circ .\)
b)\(BH = \frac{{CH}}{{\tan 28^\circ }}.\)
c)\(AB = \left( {\tan 43^\circ + \tan 28^\circ } \right)CH\).
d) Cồn cách bờ sông hai người đứng một khoảng lớn hơn \(85{\rm{ m}}{\rm{.}}\)
Có bao nhiêu giá trị của \(x\) thỏa mãn phương trình: \(\frac{2}{{x + 1}} + \frac{1}{{x - 2}} = \frac{3}{{\left( {x + 1} \right)\left( {x - 2} \right)}}\)?
Bạn An dự định mua \(2{\rm{ kg}}\) xoài và \(2{\rm{ kg}}\) vải hết \(100\) nghìn đồng. Thực tế, An đã mua \(3{\rm{ kg}}\) xoài và \(1{\rm{ kg}}\) vải hết 90 nghìn đồng. Hỏi giá tiền một kilogram xoài bao nhiêu tiền? (Đơn vị: Nghìn đồng).
Tìm nghiệm nguyên nhỏ nhất thỏa mãn bất phương trình: \(3x - \left( {6 + 2x} \right) \le 3 \cdot \left( {x + 4} \right)\).
Một chiếc đèn thả hình vành khuyên, rỗng ở giữa. Biết đường kính của đường tròn lớn là \(90\,{\rm{cm}}\), đường kính của đường tròn nhỏ là \(60\,{\rm{cm}}\). Hỏi diện tích của chiếc đèn bằng bao nhiêu mét vuông? (Kết quả làm tròn đến hàng phần trăm)
B. TỰ LUẬN (3,0 điểm)
(1,0 điểm)Cho biểu thức \(A = \frac{3}{{\sqrt a + 3}}:\left( {\frac{{\sqrt a - 2}}{{\sqrt a + 3}} + \frac{{\sqrt a - 3}}{{2 - \sqrt a }} - \frac{{9 - a}}{{a + \sqrt a - 6}}} \right)\) với \(a \ge 0,{\rm{ }}a \ne 4\) và \(a \ne 9.\)
a) Chứng minh rằng \(A = \frac{3}{{\sqrt x - 2}}\).
b) Tìm \(a\) để \(A + \left| A \right| = 0.\)
(1,5 điểm) Trên đường thẳng \(xy\), lấy lần lượt ba điểm \(A,B,C\) sao cho \(AB > BC\). Vẽ đường tròn \(\left( O \right)\) đường kính \(AB\) và đường tròn \(\left( {O'} \right)\) đường kính .
a) Gọi \(H\) là trung điểm của \(AC\). Vẽ dây \(DE\) của đường tròn \(\left( O \right)\) vuông góc với \(AC\) tại \(H\). Chứng minh tứ giác \(ADCE\) là hình thoi.
b)\(DC\) cắt đường tròn \(\left( {O'} \right)\) tại \(F\). Chứng minh rằng ba điểm \(F,B,E\) thẳng hàng.
c) Chứng minh rằng \(HF\) là tiếp tuyến của đường tròn \(\left( {O'} \right)\).
(0,5 điểm) Một công ty sản xuất dụng cụ thể thao nhận được một đơn đặt hàng sản xuất \(8\,000\) quả bóng tennis. Công ty này sở hữu một số máy móc, mỗi máy móc có thể sản xuất 30 quả bóng một giờ. Chi phí thiết lập các máy này là 200 nghìn đồng cho mỗi máy. Khi được thiết lập, hoạt động sản xuất sẽ hoàn toàn diễn ra tự động dưới sự giám sát. Số tiền phải trả cho người giám sát là \(192\,000\) nghìn đồng một giờ (người này sẽ giám sát tất cả các máy hoạt động). Số máy móc công ty nên sử dụng là bao nhiêu để chi phí sản xuất là thấp nhất?








