Bộ 5 đề thi cuối kì 1 Toán 9 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 1
21 câu hỏi
Phần 1. (3,0 điểm) Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Điều kiện xác định của phương trình \(\frac{{x + 3}}{{x + 1}} + \frac{{x - 2}}{x} = 2\) là
\(x \ne 0;\,\,x \ne 1.\)
\(x \ne 0;\,\,x \ne - 1.\)
\(x \ne 3;\,\,x \ne 2.\)
\(x \ne 0.\)
Phương trình \(5\left( {x + 2} \right)\left( {2x - 1} \right) = 0\) có mấy nghiệm?
1.
2.
3.
0.
Phương trình nào sau đây không là phương trình bậc nhất hai ẩn?
\(5x - y = 3.\)
\(\sqrt 3 x + 0y = 3.\)
\(0x + 2y = \sqrt 7 .\)
\(0x + 0y = 4.\)
Trong các hệ phương trình sau, đâu không phải là hệ phương trình bậc nhất hai ẩn?
\(\left\{ \begin{array}{l}3x - y = 5\\x + 2y = - 1\end{array} \right..\)
\(\left\{ \begin{array}{l} - 3y = 6\\3x + 5y = 15\end{array} \right..\)
\(\left\{ \begin{array}{l}{x^2} - 4{y^2} = 0\\2x + 5y = 7\end{array} \right..\)
\(\left\{ \begin{array}{l}2x - 3y = - 3\\2x + 5y = 7\end{array} \right..\)
Phát biểu “\(x\) không lớn hơn \( - 100\)” được viết là
\(x > - 100.\)
\(x \ge - 100.\)
\(x < - 100.\)
\(x \le - 100.\)
Biết rằng \(m > n\) với \(m,\,n\) bất kì. Khẳng định nào dưới đây là đúng?
\(m - 3 > n - 3.\)
\(m + 3 < n + 3.\)
\(m - 2 < n - 2.\)
\(n + 2 > m + 2.\)
Biểu thức nào sau đây có giá trị khác với các biểu thức còn lại?
\({\left( { - \sqrt 5 } \right)^2}.\)
\(\sqrt {{5^2}} .\)
\(\sqrt {{{\left( { - 5} \right)}^2}} .\)
\( - {\left( {\sqrt 5 } \right)^2}.\)
Điều kiện xác định của biểu thức \(A = \sqrt {1 - 2x} \) là
\(x \le \frac{1}{2}.\)
\(x < \frac{1}{2}.\)
\(x > \frac{1}{2}.\)
\(x \ge \frac{1}{2}.\)
Với mọi góc nhọn \(\alpha \), ta có
\(\sin \left( {90^\circ - \alpha } \right) = \cos \alpha .\)
\(\tan \left( {90^\circ - \alpha } \right) = \cos \alpha .\)
\(\cot \left( {90^\circ - \alpha } \right) = 1 - \tan \alpha .\)
\(\cot \left( {90^\circ - \alpha } \right) = \sin \alpha .\)
Cho \(\Delta MNP\) vuông tại \(N\). Hệ thức nào sau đây là đúng?
\(NP = MN \cdot \tan P.\)
\(NP = MN \cdot \cos P.\)
\(NP = MP \cdot \cos P.\)
\(NP = MP \cdot \cot P.\)
Hai đường tròn chỉ có một điểm chung được gọi là hai đường tròn
Cắt nhau.
Tiếp xúc nhau.
Ngoài nhau.
Không xác định.
Đường thẳng \(d\) cách tâm \(O\) của đường tròn \(\left( {O;\,\,4\,{\rm{cm}}} \right)\) một khoảng \({\rm{3 cm}}.\) Khi đó vị trí tương đối của \(d\) và đường tròn \(\left( {O;\,\,4\,{\rm{cm}}} \right)\) là
cắt nhau.
không giao nhau.
tiếp xúc nhau.
không kết luận được.
Phần 2. (2,0 điểm) Câu trắc nghiệm đúng sai
Trong câu 13, 14, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Vòng đầu tiên của cuộc thi “Ai là Trạng Quỳnh” gồm bộ \(20\) câu hỏi, mỗi câu trả lời đúng được cộng \(8\) điểm, mỗi câu trả lời sai bị trừ \(4\) điểm. Mỗi thí sinh bắt đầu với \(10\) điểm và cần đạt ít nhất \(90\) điểm để vào vòng tiếp theo. Gọi \(x\) là số câu mà thí sinh cần trả lời đúng trong vòng đầu tiên \(\left( {x \in {\mathbb{N}^ * }} \right)\).
a) Số câu hỏi thí sinh trả lời sai trong vòng đầu tiên là \(20 - x\) câu.
b) Số điểm thí sinh có được khi xong vòng đầu tiên là \(10 + 8x + 4\left( {20 - x} \right)\) điểm.
c) Để qua vòng tiếp theo thì điểm của thí sinh phải thỏa mãn \(10 + 8x + 4\left( {20 - x} \right) > 90\).
d) Để qua vòng tiếp theo, mỗi thí sinh cần trả lời đúng ít nhất 14 câu.
Một người quan sát một tòa nhà và đứng cách tòa nhà khoảng \[25{\rm{\;m}}\]. Góc nâng từ mắt người quan sát đến nóc tòa nhà là \[36^\circ \]. Nếu anh ta đi thêm \[5{\rm{\;m}}\] nữa, đến vị trí \[E\] nằm giữa \[C\] và \[H\], thì có góc nâng mới từ \[F\] đến nóc tòa nhà. Chiều cao \[CD\] tính từ chân đến mắt người quan sát là \[1,6{\rm{\;m}}{\rm{.}}\] (Các kết quả làm tròn đến hàng đơn vị)
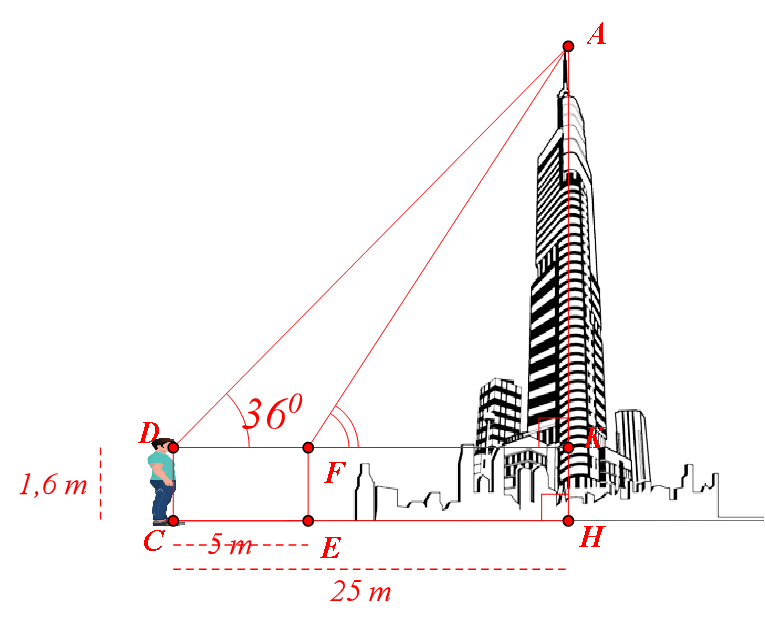
a) \[AK = KD \cdot \tan 36^\circ .\]
b) \[FK = 25{\rm{\;m}}{\rm{.}}\]
c) Độ dài tòa nhà lớn hơn 20 m.
d) Góc nâng từ \[F\] đến nóc tòa nhà khoảng \[42^\circ \].
Phần 3. (2,0 điểm)Câu hỏi trắc nghiệm trả lời ngắn
Trong các câu từ 15 đến 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Có bao nhiêu giá trị của \(x\) thỏa mãn phương trình: \(\frac{1}{{x - 2}} + 3 = \frac{{3 - x}}{{x - 2}}\)?
Bác Nam mua một thùng trái cây nặng \[\;18\,\,{\rm{kg}}\] gồm hai loại là táo và xoài. Biết táo có giá \(65\,\,000\) đồng/kg, xoài có giá \(70\,\,000\) đồng/kg và giá tiền của thùng trái cây là \(1\,\,205\,\,000\) đồng. Hỏi bác mua bao nhiêu kg táo?
Tìm giá trị nguyên nhỏ nhất của \(x\) thỏa mãn của bất phương trình \(\frac{{3x + 5}}{2} - 1 < \frac{{2x + 1}}{3} + x\).
Cho đường tròn \[\left( O \right)\] bán kính \[OA.\] Từ trung điểm \[M\] của \[OA\] vẽ dây \[BC \bot OA.\] Biết độ dài đường tròn \[\left( O \right)\] là \[4\pi {\rm{\;cm}}.\] Độ dài cung lớn \[BC\] bằng bao nhiêu? (Kết quả làm tròn đến hàng phần trăm)
B. TỰ LUẬN (3,0 điểm)
(1,0 điểm)Cho biểu thức \[T = \left( {\frac{{a\sqrt a - 1}}{{a - \sqrt a }} - \frac{{a\sqrt a + 1}}{{a + \sqrt a }}} \right):\frac{{a + 1}}{{a - 1}}\] với \[a > 0,{\rm{ }}a \ne 1\].
a) Chứng minh rằng \[T = \frac{{2\left( {a - 1} \right)}}{{a + 1}}\].
b) Tìm các giá trị nguyên của \[a\] để \[T\] nhận giá trị nguyên.
(1,5 điểm) Cho nửa đường tròn \[\left( O \right)\] đường kính \[AB\]. Lấy \[C\] nằm trên đường tròn \[\left( O \right)\]. Gọi \[K\] là trung điểm của dây cung \[BC\]. Qua \[B\] dựng tiếp tuyến với \[\left( O \right)\], cắt \[OK\] tại \[D\].
a) Chứng minh rằng \[OD \bot BC\] và \[\Delta ABC\] vuông.
b) Chứng minh \[DC\] là tiếp tuyến của đường tròn \[\left( O \right)\].
c) Vẽ \[CH \bot AB\] tại \[H\]. Gọi \[I\] là trung điểm của \[CH\]. Tiếp tuyến tại \[A\] của đường tròn \[\left( O \right)\] cắt \[BI\] tại \[E\]. Chứng minh \[E,C,D\] thẳng hàng.
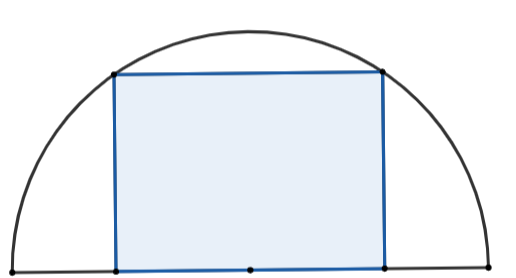
(0,5 điểm) Một khu đất có dạng nửa hình tròn với bán kính là \[14{\rm{ m}}{\rm{.}}\] Người ta muốn xây dựng một khu vui chơi hình chữ nhật ở bên trong nửa đường tròn đó như hình vẽ, biết rằng một cạnh của hình chữ nhật nằm dọc trên đường kính của nửa đường tròn. Tính diện tích lớn nhất của khu vui chơi có thể xây dựng.