Bộ 5 đề thi giữa kì 1 Toán 9 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 2
21 câu hỏi
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn (3,0 điểm)
Điều kiện xác định của phương trình \(\frac{1}{{x - 3}} - 3 = \frac{2}{{\left( {x - 3} \right)\left( {x + 4} \right)}}\) là
\[x \ne 4;{\rm{ }}x \ne - 3\].
\[x \ne 3;{\rm{ }}x \ne - 4\].
\[x \ne 3;{\rm{ }}x \ne 6\].
\[x \ne 0;{\rm{ }}x \ne - 3\].
Tổng các nghiệm của phương trình \(\left( {\frac{1}{3}x - 3} \right)\left( {x + 8} \right) = 0\) là
\(5\).
\(1\).
\( - 5\).
\( - 1\).
Trong các phương trình sau phương trình nào không phải là phương trình bậc nhất hai ẩn?
\[2x - 3y = 5.\]
\[0x + 2y = 4.\]
\[2x - 0y = 3.\]
\[0x - 0y = 6.\]
Nghiệm tổng quát của phương trình \(3x + y = 6\) là
\(\left( {x;\,\, - 3x - 6} \right)\) với \(x \in \mathbb{R}\) tùy ý.
\(\left( { - 3y + 6;\,\,y} \right)\) với \(y \in \mathbb{R}\) tùy ý.
\[\left( {x;\,\, - 3x + 6} \right)\] với \[x \in \mathbb{R}\] tùy ý.
\(\left( { - 3y - 6;\,\,y} \right)\) với \(y \in \mathbb{R}\) tùy ý.
Cặp số nào sau đây là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}2x + 3y = 3\\ - 4x - 5y = 9\end{array} \right.?\)
\(\left( {1;\,\,1} \right).\)
\(\left( {1;\,\, - 1} \right).\)
\(\left( { - 21;\,\,15} \right).\)
\(\left( {21;\,\, - 15} \right).\)
Cho hình vẽ dưới đây:
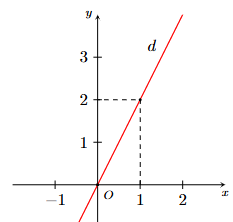
Đường thẳng \[d\] biểu diễn nghiệm của phương trình nào?
\[y = 2x.\]
\[y = - 2x.\]
\[y = 2x + 1.\]
\[y = - 2x + 1.\]
Bất đẳng thức \(m \le - 8\) có thể được phát biểu là
\(m\) lớn hơn âm 8.
\(m\) không nhỏ hơn âm 8.
\(m\) nhỏ hơn âm 8.
\(m\) không lớn hơn âm 8.
Với ba số \(a,b\) và \(c < 0\), các khẳng định sau khẳng định nào đúng?
Nếu \[a > b\] thì \(ac > bc.\)
Nếu \(a > b\) thì \(\frac{a}{c} > \frac{b}{c}.\)
Nếu \(a > b\) thì \(ac < bc.\)
Nếu \(a > b\) thì \(a + c < b + c.\)
Tam giác \[ABC\] vuông tại \[A\]. Khẳng định nào sau đây đúng?
\[AC = AB.\tan B.\]
\[AB = BC.\tan B.\]
\[AC = BC.\tan B.\]
\[AB = AC.\tan B.\]
Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = a,\,\,AC = b,\,\,AB = c\). Hệ thức nào sau đây là sai?
\(b = a \cdot \sin B = a \cdot \cos C\).
\(a = c \cdot \tan B = c \cdot \cot C\).
\({a^2} = {b^2} + {c^2}.\)
\(c = a \cdot \sin C = a \cdot \cos B\).
Cho góc \(\alpha \) thỏa mãn \(0^\circ < \alpha < 90^\circ \). Biết \(\tan \alpha = \frac{4}{3}\). Giá trị của \(\cot \left( {90^\circ - \alpha } \right)\) bằng
\(\frac{3}{4}\).
\(\frac{4}{3}\).
\(\frac{5}{3}\).
\(\frac{5}{4}\).
Cho hình bình hành \[ABCD\]có \[AC \bot AD\] và \(AD = 3,5\,;\,\,\widehat D = 50^\circ \). Hỏi diện tích của hình bình hành là bao nhiêu? (Kết quả làm tròn đến hàng phần mười)
14.
\[14,6.\]
\[14,5.\]
\[14,9.\]
Phần 2. Câu trắc nghiệm đúng sai (2,0 điểm)
Giải hệ phương trình \[\left\{ \begin{array}{l}6x - 3y = - 12\,\,\,\left( 1 \right)\\ - 2x + y = 4\,\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\] bằng phương pháp thế theo các bước:
a) Từ phương trình (2), ta có \(y = 2x + 4\).
b) Thay \(y = 2x + 4\) vào phương trình (1), ta được \(0x = 0\).
c) Phương trình \(0x = 0\) vô nghiệm.
d) Nghiệm tổng quát của hệ phương trình đã cho là \(\left( {2y + 4;\,\,y} \right)\) với \(x \in \mathbb{R}\) tùy ý.
Cho bất phương trình \(m\left( {2x + 1} \right) < 8\).
a) Bất phương trình đã cho là bất phương trình bậc nhất ẩn \(x\) với \(m \in \mathbb{R}\) tùy ý.
b) Khi \(m = 1,\) bất phương trình đã cho có nghiệm là \(x < \frac{7}{2}\).
c) Khi \(m = - 1,\) bất phương trình đã cho có nghiệm là \(x < - \frac{9}{2}\).
d) Khi \(m = - 2,\) bất phương trình đã cho có nghiệm nguyên lớn nhất là \( - 2\).
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn (2,0 điểm)
Cho phương trình \[\left( {x - 2} \right)\left( {3x + 5} \right) = \left( {2x - 4} \right)\left( {x + 1} \right)\]. Hỏi có bao nhiêu giá trị của \(x\) thỏa mãn phương trình đã cho?
Biết đường thẳng \(y = ax + b\) đi qua hai điểm \(M\left( {3;\,\, - 5} \right)\) và \(N\left( {1;\,\,2} \right).\) Tính tổng bình phương của \(a\) và \(b.\)
Số nguyên nhỏ nhất thỏa mãn bất phương trình \(x\left( {5x + 1} \right) + 4\left( {x + 3} \right) \ge 5{x^2}\) là bao nhiêu?
Cho góc nhọn \(\alpha \) thỏa mãn \(0^\circ < \alpha < 70^\circ \) và biểu thức:
\[A = \tan \alpha \cdot \tan \left( {\alpha + 10^\circ } \right) \cdot \tan \left( {\alpha + 20^\circ } \right) \cdot \tan \left( {70^\circ - \alpha } \right) \cdot \tan \left( {80^\circ - \alpha } \right) \cdot \tan \left( {90^\circ - \alpha } \right)\].
Tính giá trị của biểu thức \(A\).
B. TỰ LUẬN (3,0 điểm)
(1,0 điểm)Giải bài toán sau bằng cách lập hệ phương trình:
Đại hội Thể thao Đông Nam Á – SEA Games (South East Asian Games) là sự kiện thể thao được tổ chức 2 năm 1 lần với sự tham gia của các vận động viên trong khu vực Đông Nam Á. Việt Nam là đội chủ nhà của SEA Games 31 diễn ra từ ngày 12/5/2022 đến ngày 23/5/2022. Ở môn bóng đá nam, một bảng đấu có 5 đội A, B, C, D, E thi đấu theo thể thức vòng tròn một lượt (mỗi đội thi đấu đúng một trận với các đội còn lại). |
|
Trong mỗi trận đấu, đội thắng được 3 điểm, đội hòa được 1 điểm và đội thua được 0 điểm. Khi kết thúc bảng đấu, các đội A, B, C, D, E lần lượt có điểm số là \(10\,;\,\,9\,;\,\,6\,;\,\,4\,;\,\,0.\) Hỏi có bao nhiêu trận hòa và cho biết đó là trận hòa giữa các đội nào (nếu có)?
(1,5 điểm)
1) Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 9\) và \(\widehat {C\,} = 32^\circ .\) Tính độ dài các cạnh còn lại của tam giác \(ABC\) (kết quả làm tròn đến hàng phần trăm).
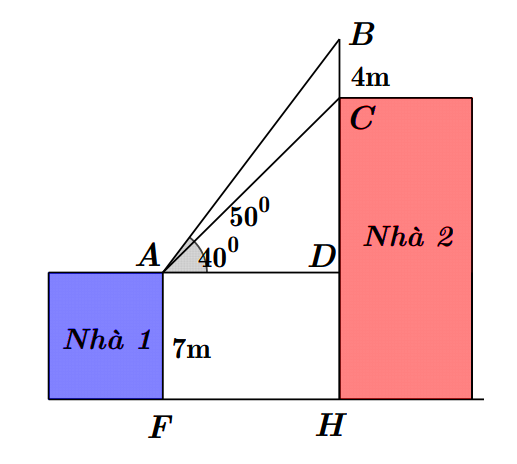
2) Cho hai tòa nhà 1 và tòa nhà 2 như hình vẽ bên. Trên nóc tòa nhà 2 có một cột ăng-ten thẳng cao \(4\) m. Từ vị trí quan sát \(A\) (trên nóc tòa nhà 1) cao \(7\) m so với mặt đất có thể nhìn thấy đỉnh \(B\) và chân \(C\) của cột ăng-ten lần lượt dưới góc \(50^\circ \) và \(40^\circ \) so với phương nằm ngang. Tính chiều cao \(CH\) của tòa nhà 2 (làm tròn kết quả đến hàng phần mười).
(0,5 điểm) Cho tam giác đều \(ABC\) có cạnh bằng \(20{\rm{\;cm}}\). Người ta cắt ở ba góc của tấm nhôm đó ba tam giác (hình vẽ) để được hình chữ nhật \(MNPQ.\) Tìm độ dài đoạn \(MB\) để hình chữ nhật \(MNPQ\) có diện tích lớn nhất.










