Bộ 5 đề thi giữa kì 1 Toán 9 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 3
21 câu hỏi
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn (3,0 điểm)
Điều kiện xác định của phương trình \[2 + \frac{1}{{x - 3}} = \frac{5}{{x + 3}}\] là
\(x \ne 3.\)
\(x \ne - 3.\)
\(x \ne 0\)và \(x \ne 3.\)
\(x \ne - 3\)và \(x \ne 3.\)
Phương trình \(\frac{3}{{4\left( {x - 5} \right)}} + \frac{{15}}{{50 - 2{x^2}}} = \frac{7}{{6x + 30}}\) có nghiệm là
\[x = 5.\]
\[x = - 5.\]
Phương trình vô nghiệm.
Phương trình vô số nghiệm.
Phương trình nào sau đây là phương trình bậc nhất hai ẩn?
\(2{x^2} + 2 = 0.\)
\(3y - 1 = 5\left( {y - 2} \right).\)
\(2x + \frac{y}{2} = 1.\)
\(3\sqrt x + {y^2} = 0.\)
Cặp số nào dưới đây là thuộc đường thẳng biểu diễn nghiệm của phương trình \[2x-5y = 19?\]
\[\left( {2\,;\,\, - 3} \right).\]
\[\left( {1\,;\,\,1} \right).\]
\[\left( {1\,;\,\, - 2} \right).\]
\[\left( {12\,;\,\, - 1} \right).\]
Cho hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{\frac{1}{2}x - \frac{1}{2}y = - 1}\\{ - 3x + 3y = 5}\end{array}} \right..\) Cho các khẳng định sau:
(i)Nhân phương trình thứ nhất của hệ với 6, rồi cộng với phương trình thứ hai ta được phương trình: \[6y = -1.\]
(ii) Nhân phương trình thứ nhất của hệ với 6, rồi cộng với phương trình thứ hai ta được phương trình: \[0x = -1.\]
(iii) Hệ phương trình đã cho vô nghiệm.
Số khẳng định đúng trong các khẳng định trên là
0.
1.
2.
3.
Phương trình \(0x + 7y = 14\) có nghiệm tổng quát là
\(\left( {x;\,\,2} \right)\) với \(x \in \mathbb{R}\).
\(\left( {2;\,\,y} \right)\) với \(y \in \mathbb{R}\).
\(\left( {x;\,\,0} \right)\) với \(x \in \mathbb{R}\).
\(\left( {0;\,\,y} \right)\) với \(y \in \mathbb{R}\).
Nếu \(a,\,\,b,\,\,c\) là ba số mà \(a < b\) và \(ac > bc\) thì \(c\) là
số âm.
số dương.
số 0.
số tùy ý.
Biển báo giao thông R.306 (hình bên báo tốc độ tối thiểu cho các xe cơ giới. Biển có hiệu lực bắt buộc các loại xe cơ giới vận hành với tốc độ không nhỏ hơn trị số ghi trên biển trong điều kiện giao thông thuận lợi và an toàn. Nếu một ô tô đi trên đường đó với tốc độ \(a\,\,\left( {{\rm{km/h}}} \right)\) thì \(a\) phải thỏa mãn điều kiện nào sau đây là đúng nhất?
\[a \le 60.\]
\[a > 60.\]
\[a \ge 60.\]
\[a = 60.\]
Cho tam giác \(MNP\) vuông tại \(M\). Khi đó \(\tan \widehat {MNP}\) bằng
\(\frac{{MN}}{{NP}}\).
\(\frac{{MP}}{{NP}}\).
\(\frac{{MN}}{{MP}}\).
\(\frac{{MP}}{{MN}}\).
Cho tam giác \[ABC\] vuông tại \[A.\] Hệ thức nào sau đây không đúng?
\(AB = BC \cdot \sin C.\)
\(AC = AB \cdot \cot C.\)
\(AB = AC \cdot \tan B.\)
\(AB = BC \cdot \cos B.\)
Cho \[\alpha ,\,\,\beta \] là số đo các góc nhọn của một tam giác vuông. Khẳng định nào sau đây là đúng?
\(\sin \alpha - \cos \alpha = 0\).
\(\tan \alpha \cdot \cot \beta = 1\).
\(\cos \alpha - \cos \beta = 0\).
\(\tan \alpha - \cot \beta = 0\).
Trong tam giác \[ABC\], nếu \(\widehat B = 30^\circ \) thì tỉ số giữa cạnh đối \(AC\) và cạnh huyền \(BC\) bằng
\(\frac{{\sqrt 3 }}{2}.\)
\(\frac{1}{2}\).
\(\frac{{\sqrt 2 }}{2}.\)
1.
Phần 2. Câu trắc nghiệm đúng sai (2,0 điểm)
Cho phương trình \[4x - 7y = - 1{\rm{ }}\left( * \right)\].
a)Hệ số \[a;\,\,b;\,\,c\] của phương trình \[\left( * \right)\] lần lượt là \[4\,;\,\, - 7\,;\,\, - 1.\]
b)Phương trình \[\left( * \right)\] là không phải phương trình bậc nhất hai ẩn vì hệ số \(b < 0\).
c)Cặp số \[\left( {0\,;\,\,5} \right)\] là nghiệm của phương trình \[\left( * \right)\].
d) Biểu diễn hình học tất cả các nghiệm của phương trình \[\left( * \right)\]là đường thẳng \[y = \frac{4}{7}x + \frac{1}{7}.\]
Cho hai số \(a,\,\,b\) và \[a > 1 > b.\]
a) \(a - 1 > 0.\) b) \(a - b < 0.\)
c) \(\left( {a - 1} \right)\left( {b - 1} \right) < 0.\) d) \(a - 2b < - 1.\)
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn (2,0 điểm)
Phương trình \(\frac{1}{{x - 1}} - \frac{7}{{x - 2}} = \frac{1}{{\left( {x - 1} \right)\left( {2 - x} \right)}}\) có bao nhiêu nghiệm?
Cho hệ phương trình \(\left\{ \begin{array}{l}x - y = 1\\3x + y = 7\end{array} \right.\) có nghiệm \[\left( {x\,;\,\,y} \right).\] Tính tổng \[x + y\].
Tìm giá trị nguyên lớn nhất của \(x\) thỏa mãn bất phương trình \[{\left( {x + 2} \right)^2}\; < x + {x^2}\;-3\].
Biết \(0^\circ < \alpha < 90^\circ ,\) tính giá trị biểu thức \[A = \frac{{\sin \alpha + 3\cos \left( {90^\circ - \alpha } \right)}}{{\sin \alpha - 2\cos \left( {90^\circ - \alpha } \right)}}.\]
B. TỰ LUẬN (3,0 điểm)
(1,0 điểm) Giải bài toán sau bằng cách lập hệ phương trình:
Anh Hoài đã đến phòng tập thể dục và tập 40 phút Yoga, sau đó nhảy Jumping jacks 10 phút và tiêu hao được 510 calo. Lần tiếp theo anh Hoài tập 30 phút Yoga và thực hiện nhảy Jumping jacks 20 phút, lượng calo tiêu hao được là 470 calo. Hỏi có bao nhiêu calo đã tiêu hao trong mỗi phút tập Yoga? Có bao nhiêu calo đã tiêu hao trong mỗi phút tập Jumping jacks?
(1,5 điểm)
1)Cho tam giác \(ABC\) có đường cao \(AH = 5\,\,{\rm{cm}},\,\,\widehat B = 70^\circ ,\,\,\widehat C = 35^\circ .\) Tính độ dài các cạnh của tam giác \(ABC\)(làm tròn kết quả đến chữ số thập phân thứ hai).
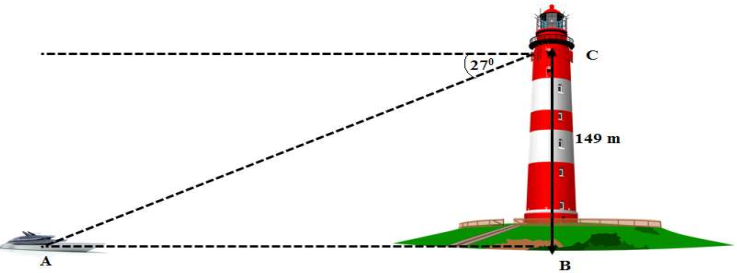
2) Một người quan sát ở đài hải đăng cao \(149\,\,{\rm{m}}\) so với mực nước biển nhìn thấy một con tàu ở xa với một góc nghiêng xuống đất là \(27^\circ .\) Hỏi tàu đang đứng cách chân hải đăng là bao nhiêu mét? (làm tròn kết quả đến hàng đơn vị)
(0,5 điểm) Một nhóm học sinh tham gia một kỳ thi và có tổng cộng 40 điểm. Nếu biết rằng không có học sinh nào có điểm dưới 10 và tổng số điểm của các học sinh là 300. Chứng minh rằng không có học sinh nào có điểm lớn hơn 30.








