Bộ 5 đề thi giữa kì 1 Toán 9 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 1
21 câu hỏi
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn (3,0 điểm)
Điều kiện xác định của phương trình \(\frac{1}{{x + 2}} + 1 = \frac{2}{{x - 1}}\) là
\[x \ne 1;{\rm{ }}x \ne - 3\].
\[x \ne 2;{\rm{ }}x \ne 1\].
\[x \ne - 3;{\rm{ }}x \ne --2\].
\(x \ne - 2;{\rm{ }}x \ne 1.\)
Phương trình \(\left( {\frac{2}{3}x + 6} \right)\left( {8 - 2x} \right) = 0\) có nghiệm là
\[x = - 9\,;\,\,x = 4\]
\[x = 4.\]
\[x = - 9.\]
\[x = 9\,;\,\,x = 4.\]
Phương trình nào sau đây không là phương trình bậc nhất hai ẩn?
\[\left( {x - 5} \right) + \left( {2y - 6} \right) = 0\].
\[5x - 3z = 6\].
\(5x - 8y = 0.\)
\[\left( {x - 2} \right)\left( {2y - 3} \right) = 3.\]
Phương trình \(0x + 7y = 14\) có nghiệm tổng quát là
\(\left( {x;\,\,2} \right)\) với \(x \in \mathbb{R}\).
\(\left( {2;\,\,y} \right)\) với \(y \in \mathbb{R}\).
\(\left( {x;\,\,0} \right)\) với \(x \in \mathbb{R}\).
\(\left( {0;\,\,y} \right)\) với \(y \in \mathbb{R}\).
Giá trị của \(a\) và \(b\) để cặp số \[\left( { - 2;\,\,3} \right)\] là nghiệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{ax + y = 5}\\{3x + by = 0}\end{array}} \right.\) là
\(\left( {a;\,\,b} \right) = \left( { - 3;\,\,3} \right)\).
\(\left( {a;\,\,b} \right) = \left( { - 2;\,\,1} \right)\).
\(\left( {a;\,\,b} \right) = \left( {2;\,\, - 4} \right)\).
\(\left( {a;\,\,b} \right) = \left( { - 1;\,\,2} \right)\).
Hình nào dưới đây biểu diễn tất cả các nghiệm của phương trình \[2x + y = 3?\]
A. 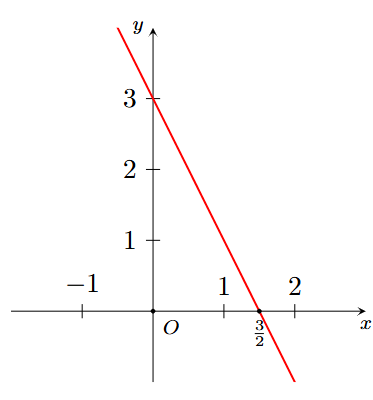
B. 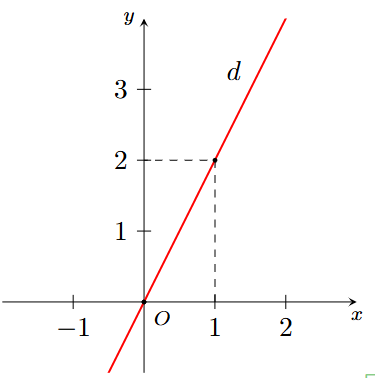
C. 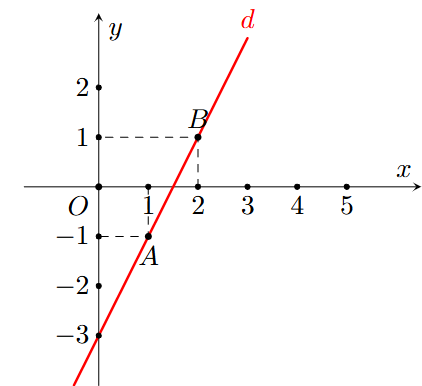
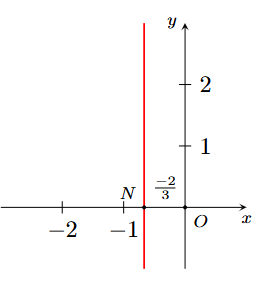
Phát biểu “\(a\) không nhỏ hơn \(b\)” được biểu diễn bằng bất đẳng thức nào dưới đây?
\(a < b.\)
\(a \ge b.\)
\(a \le b.\)
\(a > b.\)
Nghiệm \[x = 5\] thỏa mãn bất phương trình nào dưới đây?
\[5 + 7x \le 11.\]
\[2,5x - 6 > 9 + 4x.\]
\[5 + 7x \ge 15.\]
\[3 - 0,2x > 13.\]
Cho tam giác \(ABC\) vuông tại \(A\). Khi đó, \(\sin \widehat {ABC}\) bằng:
\(\frac{{AC}}{{BC}}.\)
\(\frac{{BC}}{{AC}}.\)
\(\frac{{AB}}{{BC}}.\)
\(\frac{{AB}}{{AC}}.\)
Cho tam giác \(ABC\) vuông tại \(A\). Hệ thức nào sau đây là sai?
\(BC = \frac{{AC}}{{\sin B}}.\)
\(BC = \frac{{AB}}{{\sin C}}.\)
\(BC = \frac{{AC}}{{\cos C}}.\)
\(AB = \frac{{AC}}{{\tan C}}.\)
Cho \(\alpha \) và \(\beta \) là hai góc nhọn bất kì thỏa mãn \[\alpha + \beta = 90^\circ \] và \[\sin \alpha = 0,5.\] Khẳng định nào sau đây là đúng?
\[\sin \beta = 0,5.\]
\[\cos \beta = 0,5.\]
\[\tan \beta = 0,5.\]
\[\cot \beta = 0,5.\]
Một cột đèn \(AB\) cao 6 m có bóng in trên mặt đất là \(AC\) dài \(3,5\;{\rm{m}}\). Góc (làm tròn đến phút) mà tia sáng từ đèn \(B\) tạo với mặt đất là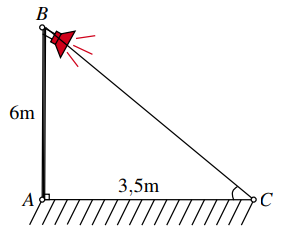
\(58^\circ 45\prime \).
\(59^\circ 50\prime \).
\(59^\circ 45\prime \).
\(59^\circ 4\prime \).
Phần 2. Câu trắc nghiệm đúng sai (2,0 điểm)
Cho phương trình \[x + 2y = 3.\]
a) Cặp số \[\left( {5;\,\, - 1} \right)\] là một nghiệm của phương trình đã cho.
b) Phương trình đã cho là phương trình bậc nhất một ẩn.
c) Tất cả nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng \(y = 3 - \frac{1}{2}x.\)
d) Phương trình đã cho có vô số nghiệm, nghiệm tổng quát là \(\left( {3 - 2y;\,\,y} \right)\) với \(y \in \mathbb{R}\) tùy ý.
Cho bất phương trình \(m\left( {5x - 2} \right) < 1\).
a) Bất phương trình đã cho là bất phương trình bậc nhất ẩn \(x\) với \(m \in \mathbb{R}\) tùy ý.
b) Khi \(m = 1,\) bất phương trình đã cho có nghiệm là \(x < \frac{3}{5}\).
c) Khi \(m = - 1,\) bất phương trình đã cho có nghiệm là \(x < \frac{1}{5}\).
d) Khi \(m = - 2,\) bất phương trình đã cho có nghiệm nguyên lớn nhất là \( - 1\).
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn (2,0 điểm)
Phương trình \(\frac{{2x - 5}}{{x + 4}} + \frac{x}{{4 - x}} = \frac{{17x - 56}}{{16 - {x^2}}}\) có bao nhiêu nghiệm?
Tìm tổng các hệ số \(x\) và \(y\) trong phản ứng hóa học đã được cân bằng sau:
\(x{\rm{KN}}{{\rm{O}}_3} \to 2{\rm{KN}}{{\rm{O}}_2} + y{{\rm{O}}_2}.\)
Tìm số tự nhiên \(x\) nhỏ nhất thỏa mãn bất phương trình \[3 < \frac{{2x - 2}}{8}\].
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 5{\rm{\;cm}}\) và đường cao \(AH = 3{\rm{\;cm}}.\) Tính số đo góc \(C\) (làm tròn kết quả đến độ).
B. TỰ LUẬN (3,0 điểm)
(1,0 điểm) Giải bài toán sau bằng cách lập hệ phương trình:
Theo các chuyên gia về sức khỏe, người trưởng thành cần đi bộ từ \(5\,\,000\) bước mỗi ngày sẽ rất tốt cho sức khỏe. Để rèn luyện sức khỏe, anh Sơn và chị Hà đề ra mục tiêu mỗi ngày một người phải đi bộ ít nhất \(6\,\,000\) bước. Hai người cùng đi bộ ở công viên và thấy rằng, nếu cùng đi trong 2 phút thì anh Sơn bước nhiều hơn chị Hà 20 bước. Hai người cùng giữ nguyên tốc độ đi như vậy nhưng chị Hà đi trong 5 phút thì lại đi nhiều hơn anh Sơn đi trong 3 phút là 160 bước. Hỏi mỗi ngày anh Sơn và chị Hà cùng đi bộ trong 1 giờ thì họ đã đạt được số bước tối thiểu mà mục tiêu đề ra hay chưa? (Giả sử tốc độ đi bộ hàng ngày của hai người không đổi)
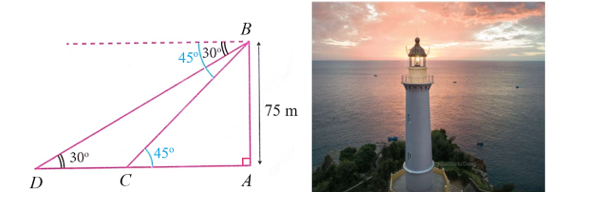
Từ trên một ngọn hải đăng cao \(75\,\,{\rm{m}}\), người ta quan sát hai lần thấy một chiếc thuyền đang hướng về phía hải đăng với góc hạ lần lượt là \(30^\circ \) và \(45^\circ \) (xem hình vẽ). Hỏi chiếc thuyền đi được bao nhiêu mét giữa hai lần quan sát? (làm tròn kết quả đến hàng đơn vị)
(0,5 điểm) Người ta dùng 100 m rào để rào một mảnh vườn hình chữ nhật để thả gia súc. Biết một cạnh của mảnh vườn là bức tường (không phải rào). Tính diện tích lớn nhất của mảnh vườn để có thể rào được.








