Bộ 5 đề thi giữa kì 1 Toán 12 Kết nối tri thức cấu trúc mới (có tự luận) có đáp án - Đề 5
21 câu hỏi
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\) có bảng biến thiên như hình sau:
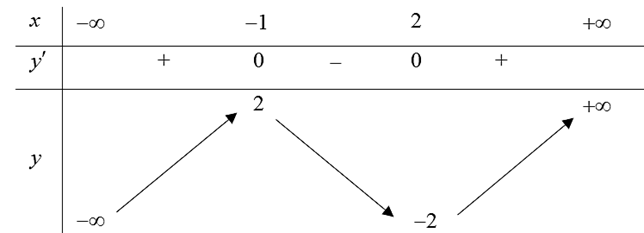
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
\(\left( { - 2;2} \right)\).
\(\left( { - 1;2} \right)\).
\(\left( { - \infty ; - 1} \right)\).
\(\left( { - \infty ;2} \right)\).
Cho hàm số \(f\left( x \right)\) có đạo hàm\(f'\left( x \right) = x\left( {x - 1} \right){\left( {x - 2} \right)^2}\left( {{x^2} - 1} \right)\), \(\forall x \in \mathbb{R}\). Số điểm cực trị của hàm số đã cho là
\(0\).
\[3\].
\(1\).
\(2\).
Cho hàm số \(y = f\left( x \right)\) có đồ thị trên đoạn \(\left[ { - 2;3} \right]\) là đường cong trong hình vẽ.
![Cho hàm số y = f(x) có đồ thị trên đoạn [ - 2;3] là đường cong trong hình vẽ.Gọi a,b lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/blobid1-1757581014.png) Gọi \(a,b\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ { - 2;3} \right]\). Tính \(S = 2{\rm{a}} + 3b\).
Gọi \(a,b\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ { - 2;3} \right]\). Tính \(S = 2{\rm{a}} + 3b\).
\(S = 2\).
\(S = - 3\).
\(S = 1\).
\(S = - 1\).
Cho hàm số \[y = \frac{{2x - 1}}{{x - 2}}\]. Phương trình đường tiệm cận đứng của đồ thị hàm số là
\(x = \frac{1}{2}\).
\(y = 2\).
\(y = \frac{1}{2}\).
\(x = 2\).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ sau.
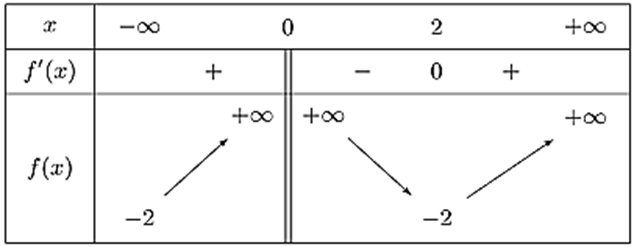
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số bằng
\(3\).
\(2\).
\(0\).
\(1\).
Đường cong trong hình vẽ là đồ thị của hàm số nào?
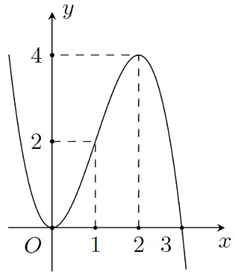
\(y = 2 + 3{x^2} - {x^3}\).
\(y = {x^3} - 3{x^2}\).
\(y = 3{x^2} - {x^3}\).
\(y = 4 + 3{x^2} - {x^3}\).
Cho hàm số \[y = f\left( x \right)\] xác định trên \(\mathbb{R}\) và có đồ thị là đường cong trong hình vẽ dưới.
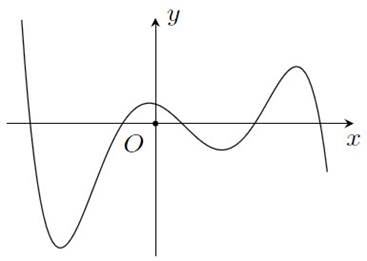
Số nghiệm của phương trình \(f\left( x \right) = 0\) là
\(4\).
\(3\).
\(2\).
\(5\).
Trong không gian, cho hình hộp \(ABCD.\,A'B'C'D'\). Vectơ đối của vectơ \[\overrightarrow {AA'} \]là
\[\overrightarrow {A'C'} \].
\[\overrightarrow {BA'} \].
\[\overrightarrow {BB'} \].
\[\overrightarrow {C'C} \].
Cho hình hộp \(ABCD.A'B'C'D'\). Hai vectơ nào sau đây cùng phương?
\(\overrightarrow {A'B} \)và \(\overrightarrow {A'B'} \).
\(\overrightarrow {B'C'} \) và \(\overrightarrow {CD} \).
\(\overrightarrow {AB} \) và \(\overrightarrow {B'C'} \).
\(\overrightarrow {AB} \) và \(\overrightarrow {D'C'} \).
Cho hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ bên dưới.
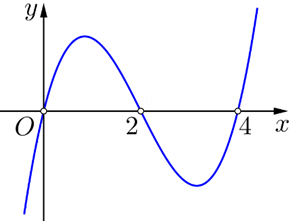
Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây?
\(\left( {4\,;\, + \infty } \right)\).
\(\left( {2\,;\,4} \right)\).
\(\left( {0\,;\,4} \right)\).
\(\left( {2\,;\, + \infty } \right)\).
Đường cong cho trong hình bên là đồ thị của hàm số nào trong các hàm số dưới đây?
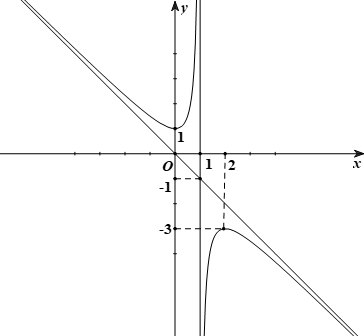
\[y = \frac{{{x^2} - 2x + 2}}{{x + 1}}\].
\[y = \frac{{{x^2} + x + 1}}{{ - x + 1}}\].
\[y = \frac{{{x^2} - x + 1}}{{ - x + 1}}\].
\[y = \frac{{ - {x^2} - x - 1}}{{2x - 1}}\].
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành, \(SA = SB = AB\). Gọi \(\alpha \) là góc giữa hai vectơ \(\overrightarrow {CD} \) và \(\overrightarrow {AS} \). Tính \(\cos \alpha \).
\[ - \frac{1}{2}\].
\[\frac{1}{2}\].
\[\frac{{\sqrt 3 }}{2}\].
\[ - \frac{{\sqrt 3 }}{2}\].
C. TRẢ LỜI NGẮN. Thí sinh trả lời câu 1 đến câu 4.
Cho hàm số \(y = \frac{{4x - 5}}{{x + 1}}\) có đồ thị \(\left( H \right)\). Gọi \(M\left( {{x_0};{y_0}} \right)\) với \({x_0} < 0\) là một điểm thuộc đồ thị \(\left( H \right)\) thỏa mãn tổng khoảng cách từ \(M\) đến hai đường tiệm cận của \(\left( H \right)\) đạt giá trị nhỏ nhất bằng \(6\). Tính giá trị của biểu thức \(S = {\left( {{x_0} + {y_0}} \right)^2}\) .
Cho hàm số phân thức: \[y = f\left( x \right) = \frac{{ - {x^2} + ax + b}}{{x - 1}}\] có đồ thị \(\left( C \right)\). Biết \(\left( C \right)\) đi qua điểm \(A\left( {0;5} \right)\) và nhận điểm \(I\left( {1;1} \right)\) làm tâm đối xứng. Tính \(T = \frac{a}{b}\) (làm tròn kết quả đến hàng phần chục).
Xác định giá trị lớn nhất của hàm số \(y = x + \frac{9}{{x - 1}}\)trên đoạn \(\left[ { - 4;\, - 1} \right]\).
Cho hình lăng trụ \(ABC.A'B'C'\), \(M\) là trung điểm của \(BB'\). Đặt \(\overrightarrow {CA} = \vec a\), \(\overrightarrow {CB} = \vec b\), \(\overrightarrow {AA'} = \vec c\). Biết \(\overrightarrow {AM} = m\vec a + n\vec b + p\vec c\). Tính \(26m + 3n - 4p\).
PHẦN II. TỰ LUẬN
Một nhà sản xuất cần làm những hộp đựng hình trụ có thể tích \[330{\rm{ml}}.\] Tìm bán kính của hộp đựng để chi phí vật liệu dùng để sản xuất là nhỏ nhất (đơn vị: cm).
Chi phí nhiên liệu của một chiếc tàu chạy trên sông được chia làm hai phần. Phần thứ nhất không phụ thuộc vào vận tốc và bằng 480 nghìn đồng trên 1 giờ. Phần thứ hai tỉ lệ thuận với bình phương của vận tốc, khi \(v = 10\) (km/giờ) thì phần thứ hai bằng 10 nghìn đồng/giờ. Biết tàu chạy với vận tốc \(v = 30\) (km/giờ), tổng chi phí nhiên liệu trên 1 km đường sông là bao nhiêu nghìn đồng?
B. TRẮC NGHIỆM ĐÚNG - SAI. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\)\(\left( {a \ne 0} \right)\) và có đồ thị là đường cong như hình.
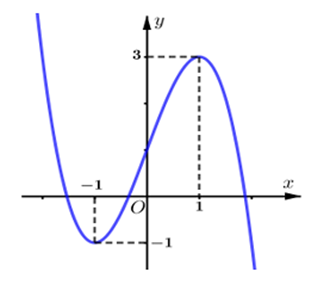
a) Hệ số \[a < 0\].
b) Đồ thị hàm số \(y = f\left( x \right)\) có điểm cực tiểu là \(\left( {1;\,3} \right)\).
c) Hàm số đồng biến trên khoảng \(\left( { - 1;\,1} \right)\).
d)\[f\left( 3 \right) = - 5\].
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(1\).
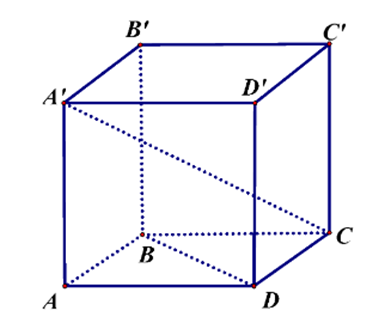
a)\(\overrightarrow {BD} = \overrightarrow {B'D'} \).
b)\(\left| {\overrightarrow {A'C} } \right| = \left| {\overrightarrow {AC'} } \right| = \sqrt 3 \).
c)\(\overrightarrow {A'C} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {D'D} \).
d) \(\overrightarrow {A'C} \cdot \overrightarrow {BD} = \sqrt 2 \).
Một chất điểm ở vị trí đỉnh \(A\) của hình lập phương \(ABCD.A'B'C'D'\). Chất điểm chịu tác động bởi ba lực \(\overrightarrow a ,\,\overrightarrow b ,\,\overrightarrow c \) lần lượt cùng hướng với \(\overrightarrow {AD} ,\,\overrightarrow {AB} ,\,\overrightarrow {AC'} \) như hình vẽ.
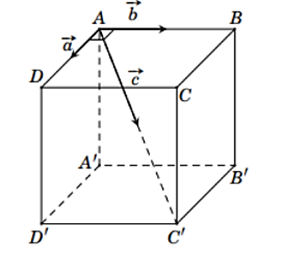
Độ lớn của các lực \(\overrightarrow a ,\,\overrightarrow b ,\,\overrightarrow c \) tương ứng là 10 N, 10 N và 20 N. Tính độ lớn hợp lực của các lực \(\overrightarrow a ,\,\overrightarrow b ,\,\overrightarrow c \).








