Bộ 20 đề thi Giữa kì 1 Toán 12 Kết nối tri thức có đáp án - Đề 13
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Trong không gian Oxyz, cho \(\vec a = \left( {1; - 2;3} \right)\) và \(\vec b = \left( {3;0;4} \right)\). Tính \(\vec a.\vec b\).
36.
5.
15.
9.
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ . Giá trị nhỏ nhất của hàm số \[f\left( x \right)\] trên đoạn \(\left[ {0;\,4} \right]\) là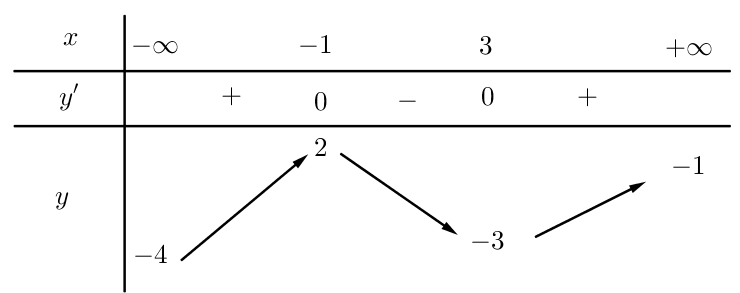
\( - 1\).
\( - 3\).
\(f\left( 0 \right)\).
\( - 4\).
Trong các hàm số sau, hàm nào đồng biến trên \(\mathbb{R}\)?
\(y = {x^3} - x\).
\(y = {x^3} + x\).
\(y = {x^4} + 2{x^2}\).
\(y = {x^2} + 1\).
Trong không gian \[{\rm{Oxyz}}\], cho hai điểm \(A\left( {\,2;\, - 1;\,0\,} \right)\), \(B\left( {0;\,1;\, - 2} \right)\). Tìm tọa độ trung điểm \(M\) của đoạn thẳng \[AB\]
\(M\left( { - 2;\,2;\, - 2} \right)\).
\(M\left( {2;\,0;\, - 2} \right)\).
\(M\left( {1;\,0;\, - 1} \right)\).
\(M\left( { - 1;\,1;\, - 1} \right)\)
Trong không gian với hệ trục tọa độ Oxyz, cho hình bình hành \(ABCD\). Biết \(A\left( {2\,;\,1;\, - 3} \right)\), \(B\left( {0\,;\, - 2\,;\,5} \right)\) và \(C\left( {1\,;\,1\,;\,3} \right)\). Diện tích hình bình hành \(ABCD\) là
\(\frac{{\sqrt {349} }}{2}\).
\(\sqrt {87} \).
\(\sqrt {349} \).
\(2\sqrt {87} \).
Cho hàm số có bảng biến thiên như sau: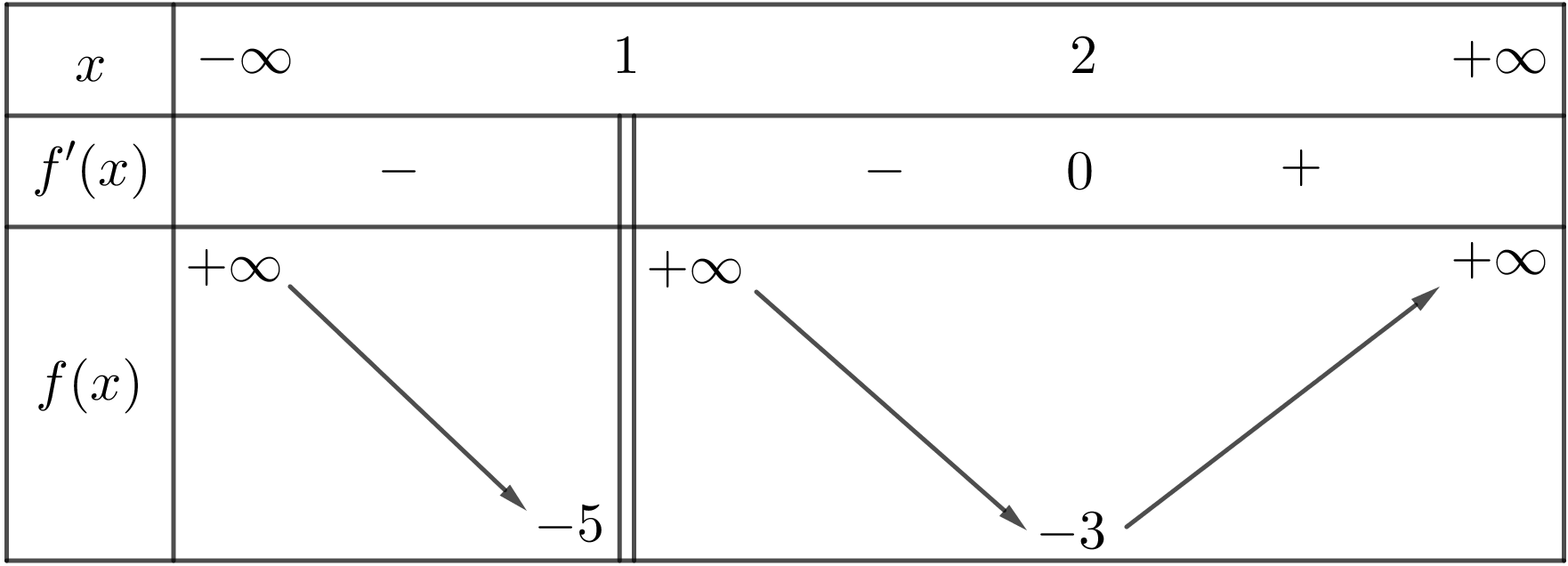
Số các đường tiệm cận (tiệm cận đứng và tiệm cận ngang) của đồ thị hàm số đã cho bằng
\(2\).
\(4\).
\(1\).
\(3\).A
Đồ thị của hàm số \(y = \frac{{2x + 1}}{{3 - x}}\)có tâm đối xứng là:
\(I\left( {3; - 1} \right)\).
\(I\left( {3; - 2} \right)\).
\(I\left( {3;2} \right)\).
\(I\left( { - 2;3} \right)\).
Hàm số nào trong bốn hàm số sau có bảng biến thiên như hình vẽ sau?
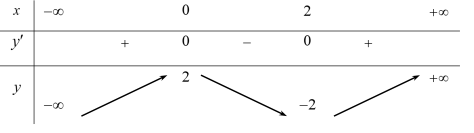
\[y = {x^3} - 3x + 2\].
\[y = {x^3} + 3{x^2} - 1\].
\[y = - {x^3} + 3{x^2} - 1\].
\[y = {x^3} - 3{x^2} + 2\].
Cho hình lăng trụ ABC.A'B'C'. Đặt \(\overrightarrow {AB} = \vec a,\,\,\overrightarrow {AA'} = \vec b,\,\,\overrightarrow {AC} = \vec c.\) Khẳng định nào sau đây đúng?
\(\overrightarrow {B'C} = - \vec a - \vec b + \vec c\).
\(\overrightarrow {B'C} = - \vec a + \vec b - \vec c\).
\(\overrightarrow {B'C} = - \vec a + \vec b + \vec c\).
\(\overrightarrow {B'C} = \vec a + \vec b - \vec c\).
Cho hàm số \[y = \frac{{mx - {m^2} - 2}}{{ - x + 1}}\] (\[m\] là tham số thực) thỏa mãn \[\mathop {\max }\limits_{\left[ { - 4; - 2} \right]} y = \frac{{ - 1}}{3}\]. Mệnh đề nào sau dưới đây đúng?
\[1 \le m < 3\].
\[ - 3 < m < \frac{{ - 1}}{2}\].
\[\frac{{ - 1}}{2} < m < 0\].
\[m > 4\].
Cho hàm số \(y = f(x)\) xác định trên đoạn \(\left[ {a;b} \right],\) có đồ thị của hàm số \(y = f'(x)\) như hình vẽ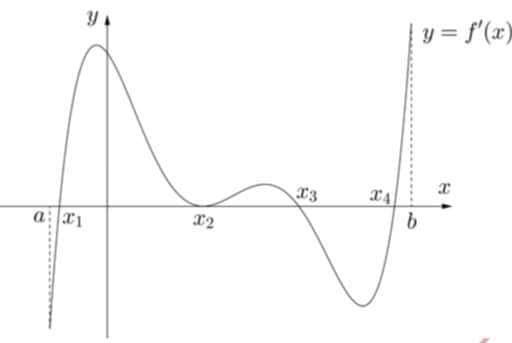
Số điểm cực trị của hàm số \(y = f(x)\)trên đoạn \(\left[ {a;b} \right]\)là
\(4.\)
\(3.\)
\(2.\)
\(1.\)
Trong không gian với hệ tọa độ Oxyz, cho các điểm \(A\),\(B\),\(\,C\) có tọa độ thỏa mãn \(\overrightarrow {OA} = \overrightarrow i + \overrightarrow j + \overrightarrow k \), \(\overrightarrow {OB} = 5\overrightarrow i + \overrightarrow j - \overrightarrow k \), \(\overrightarrow {BC} = 2\overrightarrow i + 8\overrightarrow j + 3\overrightarrow k \). Tọa độ điểm \(D\) để tứ giác \(ABCD\) là hình bình hành là
\(D\left( {3\,;\,1\,;\,5} \right)\).
\(D\left( {1\,;\,2\,;\,3} \right)\).
\(D\left( {3\,;\,9\,;\,4} \right)\).
\(D\left( { - 2\,;\,8\,;\,6} \right)\).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Trong không gian với hệ trục tọa độ Oxyz, cho hình hộp ABCD.A'B'C'D' có \(A\left( {1\,;2\,;3} \right)\); \(B\left( {4\,;5\,;6} \right)\); \(C\left( { - 3\,;2\,; - 1} \right)\) và \(D'\left( {0\,; - 3\,;5} \right)\). \(M\) là trung điểm \(CC'\). Khi đó
a) Tọa độ tâm của hình hộp là \(\left( {2\,;1\,;\frac{{11}}{2}} \right)\).
b) Tọa độ điểm \(C'\left( {9\,;4\,;10} \right)\).
c) \(\overrightarrow {BD'} = \overrightarrow {BA} + \overrightarrow {AD} + \overrightarrow {CC'} \).
d) \(\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {AD} + \frac{1}{2}\overrightarrow {AA'} \).
Cho hàm số \(y = f\left( x \right) = \frac{{a{x^2} + bx + c}}{{x + n}}\left( {a \ne 0} \right)\) có đồ thị là đường cong trong hình bên.
a) Hàm số nghịch biến trên các khoảng \(\left( { - 1;1} \right)\) và \(\left( {1;3} \right)\).
b) Phương trình \(f\left( x \right) = {m^2} + 2\) luôn có hai nghiệm phân biệt lớn hơn 1 với mọi giá trị của tham số \(m\).
c) Giá trị cực tiểu của hàm số là \({y_{CT}} = - 6\).
d) Tiệm cận xiên của đồ thị hàm số là \(y = x - 3\).
Cho hàm số \(y = f(x)\), \((a \ne 0)\) có đồ thị như hình vẽ sau :
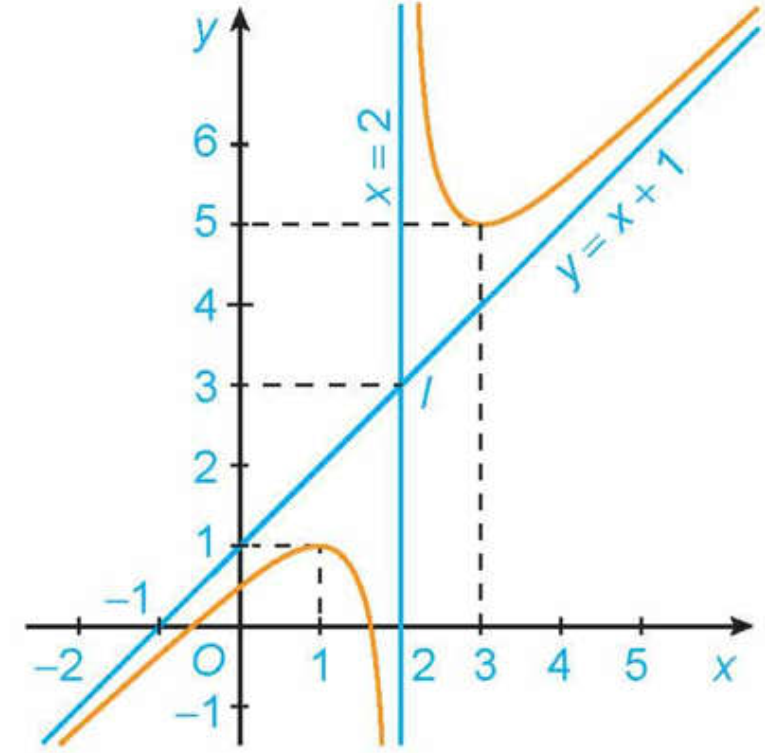
a) Hàm số đã cho có hai điểm cực trị.
b) Đường thẳng \(x + y + 1 = 0\) là tiệm cận xiên của đồ thị hàm số.
c) Tâm đối xứng của đồ thị hàm số là điểm \(I(2;3)\).
d) Số điểm cực trị của hàm số \(y = \left| {f(x)} \right|\) là 4.
Một sợi dây kim loại dài \(60cm\) được cắt thành hai đoạn. Đoạn dây thứ nhất uốn thành hình vuông cạnh \(a\), đoạn dây thứ hai uốn thành đường tròn bán kính \(r\) (hình vẽ).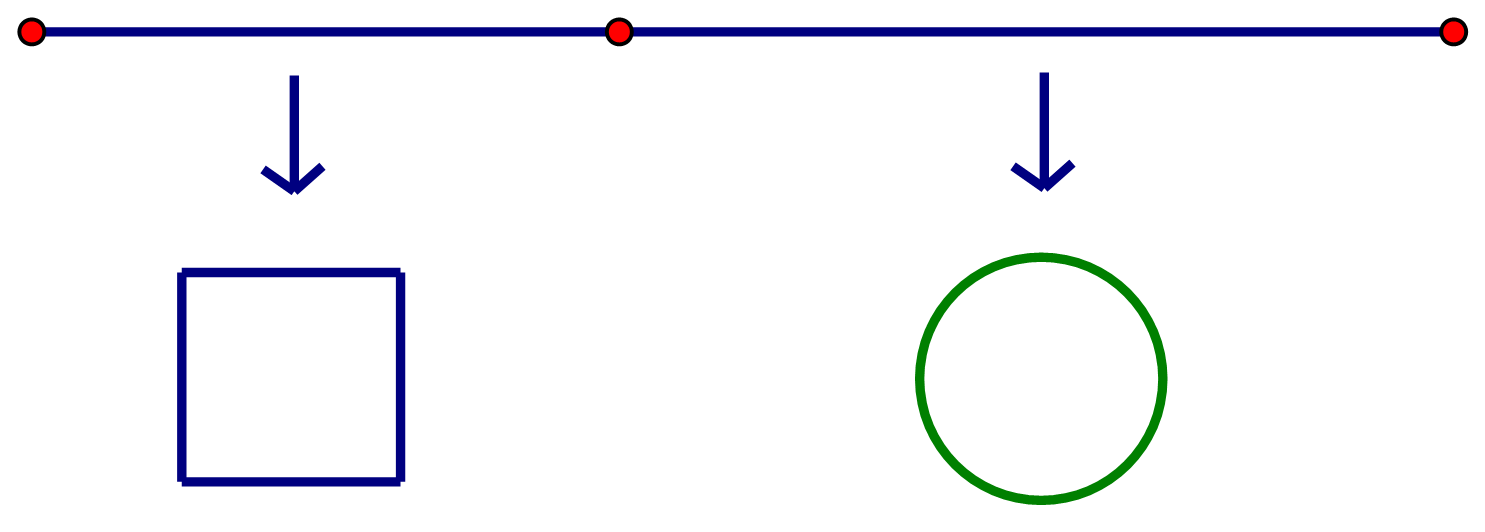
a) Điều kiện \(\,0 < a < 15\).
b) Chu vi đường tròn tạo được là \(\,2\pi r = 60 - 2a\)
c) Tổng diện tích của hình vuông và hình tròn nhỏ nhất khi tỉ số \(\frac{a}{r} = \frac{1}{2}\).
d) Bán kính đường tròn tạo được là \(\,r = \frac{{30 - 2a}}{\pi }\).
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Hai chất điểm \(A\) và \(B\) chuyển động thẳng đều cùng hướng về \(O\) (như hình vẽ), biết rằng vận tốc \({V_B} = \frac{{{V_A}}}{{\sqrt 3 }}\) và góc . Biết rằng khi khoảng cách giữa hai chất điểm \(A\) và \(B\) là nhỏ nhất thì số đo góc \(\widehat {BAO} = \gamma .\)Tìm \(\gamma .\)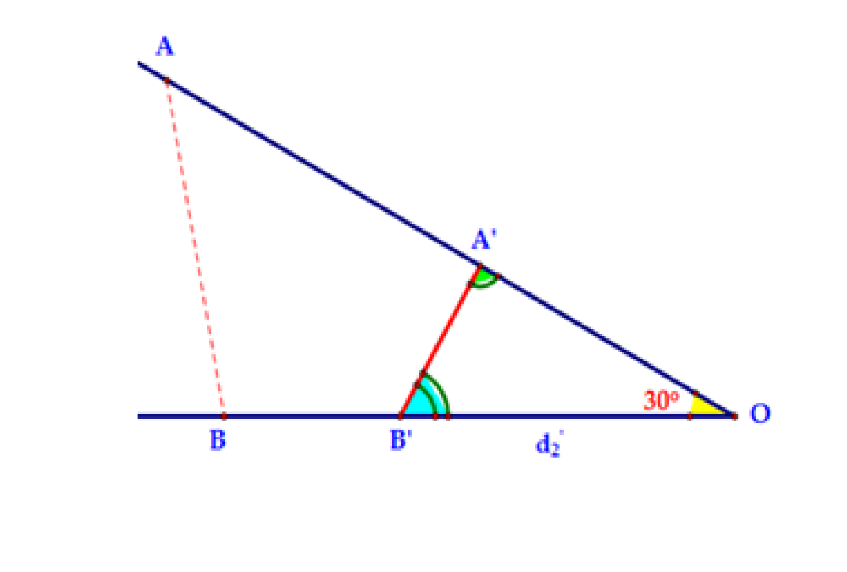
Trận bóng đá giao hữu giữa đội tuyển Việt Nam và Thái Lan ở sân vận động Mỹ Đình có sức chứa 55 000 khán giả. Ban tổ chức bán vé với giá mỗi vé là 100 nghìn đồng, số khán giả trung bình đến sân xem bóng đá là 27 000 người. Qua thăm dò dư luận, người ta thấy rằng mỗi khi giá vé giảm thêm 10 nghìn đồng, sẽ có thêm khoảng 3 000 khán giả. Hỏi ban tổ chức nên đặt giá vé là bao nhiêu để doanh thu từ tiền bán vé là lớn nhất với đơn vị tính giá vé là nghìn đồng?
Hai chiếc máy bay không người lái cùng bay lên tại một địa điểm. Sau một thời gian bay, chiếc máy bay thứ nhất cách điểm xuất phát về phía Bắc \(20\left( {km} \right)\) và về phía Tây \(10\left( {km} \right)\), đồng thời cách mặt đất \(0,7\left( {km} \right)\). Chiếc máy bay thứ hai cách điểm xuất phát về phía Đông \(30\left( {km} \right)\) và về phía Nam \(25\left( {km} \right)\), đồng thời cách mặt đất \(1\left( {km} \right)\). Xác định khoảng cách giữa hai chiếc máy bay (đơn vị km, làm tròn đến hàng đơn vị).
Một khu vực trồng hoa được xây dựng trong khu du lịch sinh thái. Trong mô hình minh họa (như hình vẽ bên), nó được giới hạn bởi các trục tọa độ và đồ thị \(\left( C \right)\) của một hàm số bậc ba. Biết rằng đồ thị \(\left( C \right)\) đi qua các điểm \(A\left( {0;8} \right),B\left( {2;5,4} \right),K\left( {5;6,75} \right)\) và \(H\left( {8;0} \right)\). Trong khu du lịch sinh thái có một con đường chạy dọc theo đường thẳng \(d:y = - \frac{{13}}{9}x + \frac{{169}}{9}\). Tìm hoành độ của điểm \(M\) thuộc \(\left( C \right)\) sao cho khoảng cách từ \(M\) đến \(d\) là nhỏ nhất (làm tròn kết quả đến hàng phần trăm).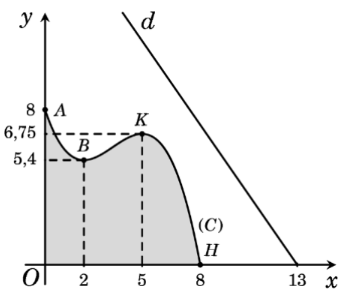
Cho ba lực \(\overrightarrow {{F_1}} = \overrightarrow {MA} ,\overrightarrow {{F_2}} = \overrightarrow {MB} ,\overrightarrow {{F_3}} = \overrightarrow {MC} \) cùng tác động vào một ô tô tại điểm \(M\) và ô tô đứng yên. Cho biết cường độ hai lực \({\vec F_1},{\bar F_2}\) đều bằng 25 N và góc . Khi đó cường độ lực \({\vec F_3}\) là (Kết quả làm tròn đên hàng phần mười)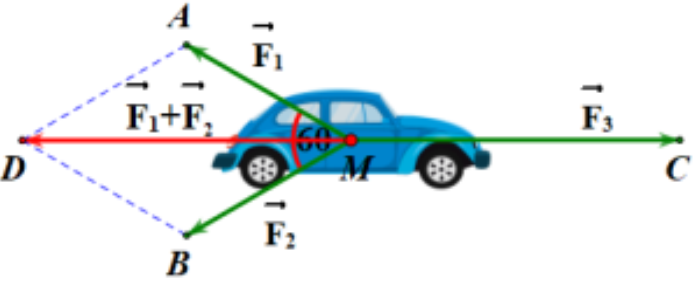
Khi loại thuốc A được tiêm vào bệnh nhân, nồng độ \[mg/l\]của thuốc trong máu sau \[x\]phút (kể từ khi bắt đầu tiêm) được xác định bởi công thức: \[C(x) = \frac{{30x}}{{{x^2} + 2}}\].
Để đưa ra những lời khuyên và cách xử lí phù hợp cho bệnh nhân, ta cần tìm khoảng thời gian mà nồng độ của thuốc trong máu đang tăng. Em hãy cho biết hàm nồng độ thuốc trong máu \[C(x)\] đạt giá trị cực đại là bao nhiêu trong khoảng thời gian \[6\] phút sau khi tiêm (kết quả làm tròn đến hàng phần mười)?
