Bộ 20 đề thi Giữa kì 1 Toán 12 Kết nối tri thức có đáp án - Đề 18
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
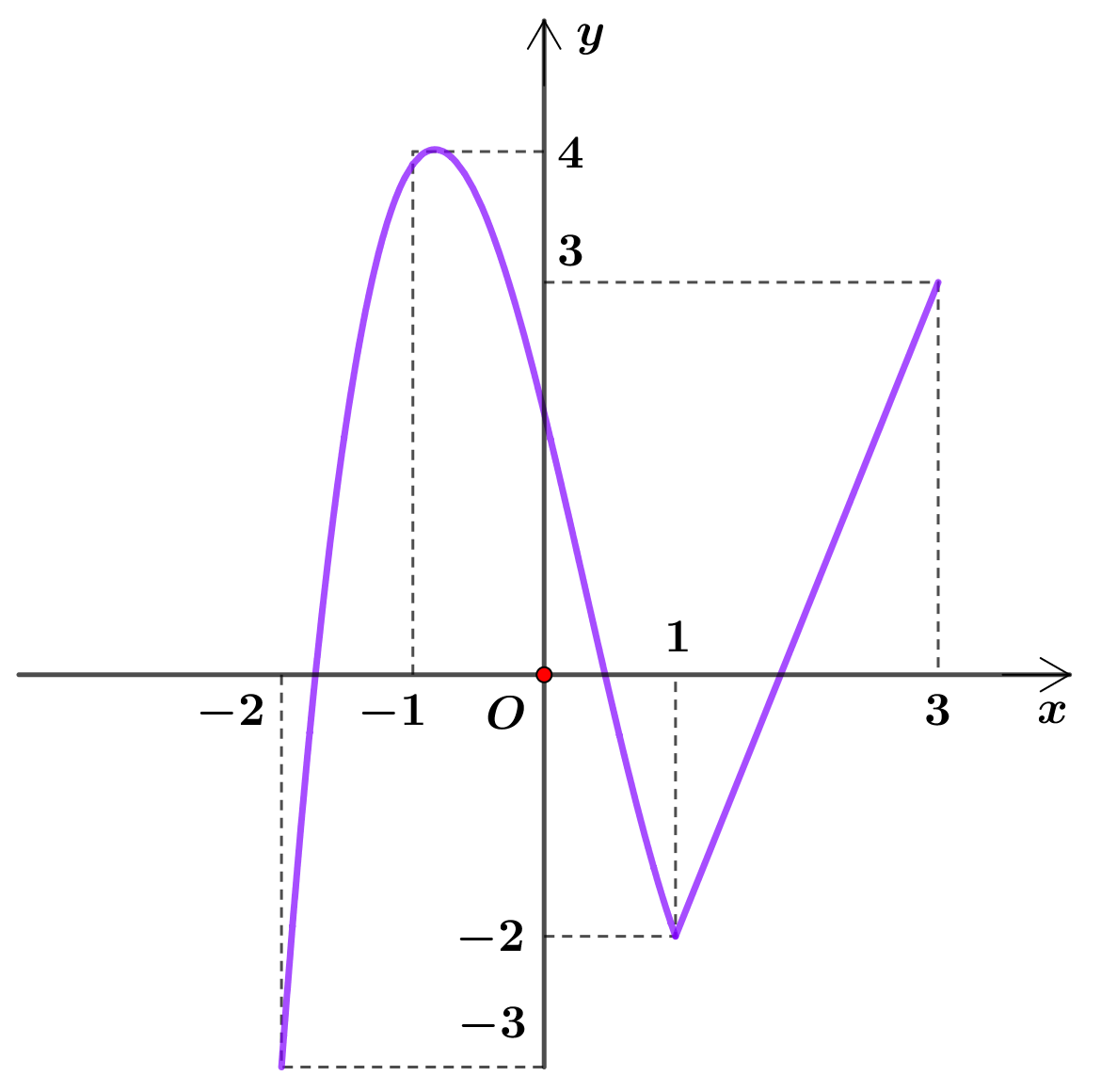
Cho hàm số \(f\left( x \right)\)liên tục trên đoạn \(\left[ { - 2;3} \right]\) có đồ thị như hình vẽ dưới đây.
Gọi \(m,\,\,M\)lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số trên đoạn \(\left[ { - 2;3} \right]\). Giá trị của \(2m - 3M\) bằng:
\( - 16.\)
\( - 18.\)
\( - 15.\)
\( - 13.\)
Trong không gian Oxyz, cho mặt cầu \((S):{x^2} + {y^2} + {z^2} + 2x - 2z - 7 = 0\). bán kính của mặt cầu đã cho bằng
\(\sqrt 7 \).
\(\sqrt {15} \).
\(9\).
\(3\).
Trong không gian tọa độ \(x\), cho vectơ \[\overrightarrow u = \left( {3;\,0;\,1} \right)\], \[\overrightarrow v = \left( {2;\,1;\,0} \right)\]. Tính tích vô hướng \[\,\overrightarrow u .\,\overrightarrow v \].
\[\,\overrightarrow u .\,\overrightarrow v = 6\].
\[\,\overrightarrow u .\,\overrightarrow v = - 6\].
\[\,\overrightarrow u .\,\overrightarrow v = 0\].
\[\,\overrightarrow u .\,\overrightarrow v = 8\].
Trong không gian Oxyz, cho \(\Delta ABC\)với \(A\left( {1\,; - 4\,;\,1} \right),\,B\left( {1\,;\,0\,;\,2} \right),\,C\left( {1\,;\,1\,;\,3} \right).\)Khi đó tọa độ trọng tâm\(G\) của \(\Delta ABC\)bằng
\(G\left( {\frac{1}{3};\, - \frac{5}{3};\,\frac{4}{3}} \right)\).
\(G\left( {\frac{1}{3};\, - 1;\,0} \right)\).
\(G\left( {\frac{3}{2}\,;\, - \frac{3}{2};\,3} \right)\).
\(G\left( {1;\, - 1;\,2} \right)\).
Hàm số nào sau đây nghịch biến trên \(\mathbb{R}\)?
\(y = \sin x\).
\(y = \sqrt {1 - x} \).
\(y = 1 - {x^3}\).
\(y = \frac{1}{x}\).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau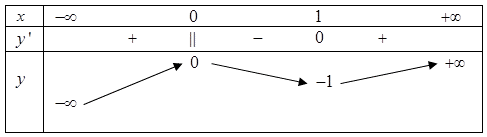
Số đường tiệm cận ngang của đồ thị hàm số là
\[0\].
\[1\].
\[2\].
\[3\].
Bảng biến thiên sau là của hàm số nào?
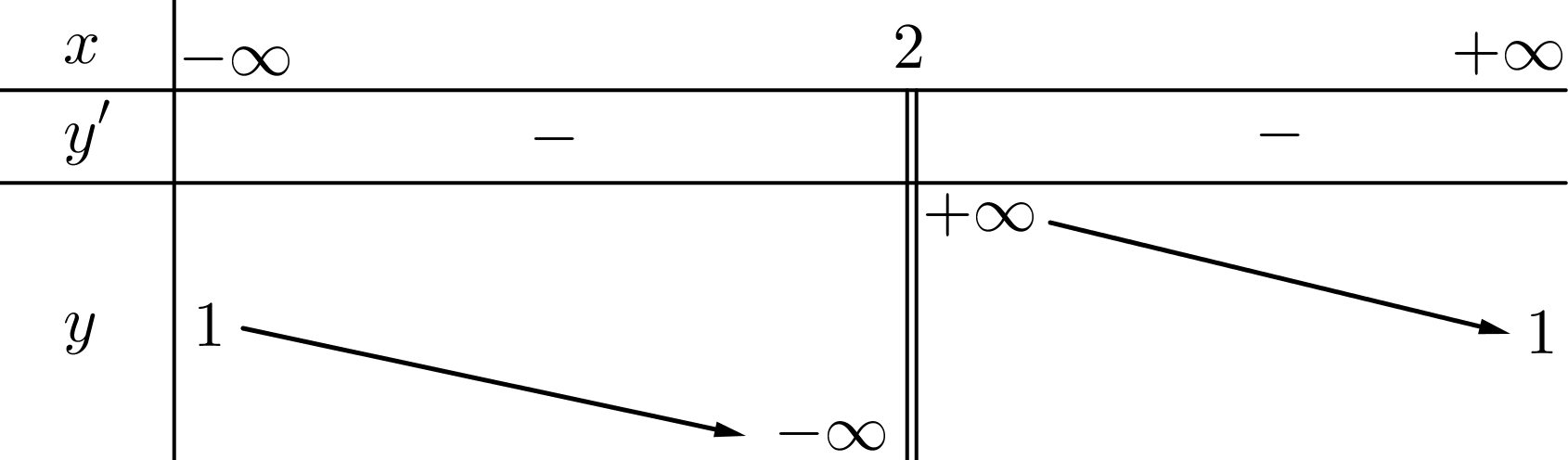
\[y\, = \,\frac{{x\, + \,3}}{{2\, + \,x}}\].
\[y\, = \,\frac{{2x\, + \,1}}{{x\, - \,2}}\].
\[y\, = \,\frac{{x\, + \,1}}{{2x\, + \,1}}\].
\[y\, = \,\frac{{x\, + \,1}}{{x\, - \,2}}\].
Cho hàm số \(y = f\left( x \right)\) có \(y' = {\left( {x - 3} \right)^3}{\left( {2x + 1} \right)^2}\left( {3x + 1} \right)\). Số điểm cực trị của hàm số \(y = f\left( x \right)\) là
\(3\).
\(2\).
\(4\).
\(6\).
Cho hàm số \(y = f\left( x \right)\)có đồ thị như đường cong ở hình bên. Xác định tọa độ tâm đối xứng I của đồ thị.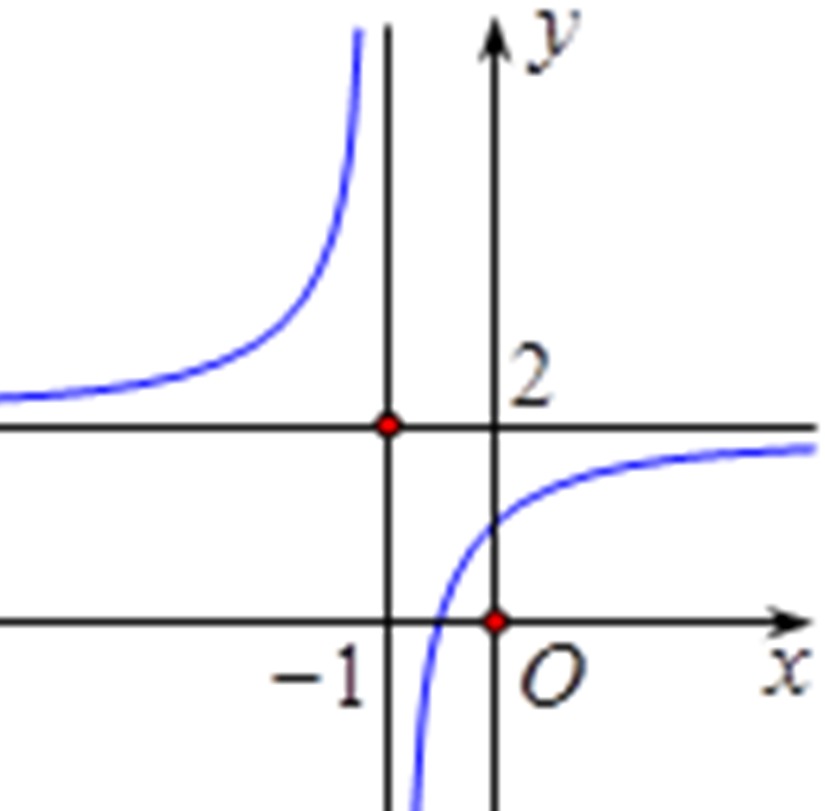 
I (0;2).
I (-1;2).
I (2;-1).
I (-1;0).
Cho hàm số \(y = \frac{{x + m}}{{x - 1}}\) (\(m\) là tham số thực) thỏa mãn \(\mathop {\min }\limits_{[2;4]} y = 3.\) Mệnh đề nào dưới đây đúng?
\(m > 4\)
\(1 \le m < 3\)
\(m < - 1\)
\(3 < m \le 4\)
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi G là điểm thỏa mãn:\[\overrightarrow {GS} + \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \]. Trong các khẳng định sau, khẳng định nào đúng:
\[\overrightarrow {GS} = 5\overrightarrow {OG} \].
G, S, O không thẳng hàng.
\[\overrightarrow {GS} = 3\overrightarrow {OG} \].
\[\overrightarrow {GS} = 4\overrightarrow {OG} \].
Cho 3 điểm \(M\left( {2;0;0} \right)\), \(N\left( {0; - 3;0} \right)\), \(P\left( {0;0;4} \right)\). Nếu \[MNPQ\] là hình bình hành thì tọa độ của điểm \(Q\) là
\(\left( {3;4;2} \right)\).
\(\left( {2;3; - 4} \right)\).
\(\left( { - 2; - 3; - 4} \right)\).
\(\left( {2;3;4} \right)\).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Một cửa hàng bán quả vải thiều của Bắc Giang với giá bán là \(30000\) đồng/ 1kg. Giá nhập vào là \(16000\) đồng/1 kg. Với giá này cửa hàng ước chừng bán được 100 kg/ ngày. Cửa hàng dự định giảm giá bán, ước tính cứ giảm \(1000\) đồng/ 1kg thì số vải thiều bán được sẽ tăng thêm là 10kg.
a) Gọi \(x\) là giá tiền mà cửa hàng dự định bán \(\left( {16 \le x \le 30} \right)\), khi đó lợi nhuận theo ngày của cửa hàng được xác định bởi hàm số \(f\left( x \right) = \left( {x - 16} \right)\left( {400 - 10x} \right)\).
b) Lợi nhuận tối đa theo ngày của cửa hàng là \(1600000\) đồng.
c) Nếu giá bán là \(20000\) đồng/ 1kg, khi đó cửa hàng bán được 250kg / ngày.
d) Nếu giữ nguyên giá ban đầu, lợi nhuận theo ngày của cửa hàng là \(1400000\)đồng.
Cho hàm số \(y = \frac{{{x^2} + 3x + 3}}{{x + 2}}\) có đồ thị là đường cong \(\left( C \right)\).
a) Biết hàm số có 2 điểm cực trị khi đó tổng của giá trị cực đại và giá trị cực tiểu bằng \( - 4\).
b) Đường tiệm cận xiên của đồ thị hàm số đi qua điểm \(A\left( {0;1} \right)\).
c) Phương trình tiếp tuyến với \(\left( C \right)\) vuông góc với đường thẳng \(x - 3y - 6 = 0\) đi qua điểm \(B\left( { - \frac{3}{2},\frac{3}{2}} \right)\).
d) Để phương trình \({x^2} + 3x + 3 = m\left| {x + 2} \right|\) có 4 nghiệm phân biệt thì \(m > 2\).
Cho hàm số \(y = \frac{{ - ax + 20}}{{bx - c}}\,\,(\,a,\,b,\,c \in \mathbb{R})\)có bảng biến thiên như hình bên dưới.
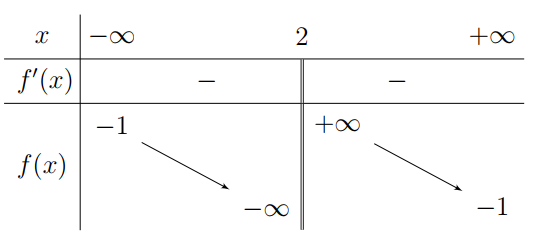
a) Tập xác định của hàm số là \(\mathbb{R}\backslash \left\{ 2 \right\}\).
b) Hàm số nghịch biến trên \(\mathbb{R}\).
c) Đồ thị hàm số cắt trục hoành tại điểm có hoành độ \(x < 2\).
d) Giá trị tổng \(2a + 2b + c\)thuộc khoảng\(\left( {0;\,60} \right)\).
Cho hình lăng trụ \(ABC \cdot A'B'C'\) có đáy \(ABC\) là tam giác đều cạnh bằng 2 như hình vẽ. Hình chiếu vuông góc của \(A'\) lên \(\left( {ABC} \right)\) trùng với trung điểm cạnh \(AB\), góc \(\widehat {A'AO} = {60^ \circ }\). Với hệ toạ độ \(Oxyz\) được thiết lập như hình bên (gốc tọa độ \(O\) trùng với trung điểm của đoạn \(BC\)), hãy xét tính đúng sai của các khẳng định sau:
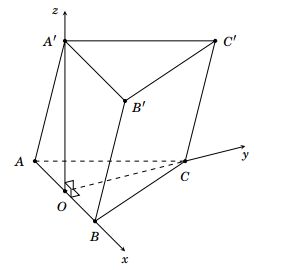
a) Tọa độ điểm \(A\left( { - 1;0;0} \right)\).
b) Tọa độ điểm \(C\left( {0;\sqrt 3 ;0} \right)\).
c) Tọa độ điểm \(A'\left( {0; - 1;\sqrt 3 } \right)\).
d) Tọa độ điểm \(C'\left( {1;\sqrt 3 ;\sqrt 3 } \right)\).
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Một đường ray tàu lượn trong khu vui chơi giải trí có hình dáng được mô phỏng theo đồ thị của hàm số \(y = {x^3} - 3x + 2\), ký hiệu là (C). Để đảm bảo an toàn và tính thẩm mỹ, người ta chọn hai điểm \(A(a;b)\) và \(B(c;d)\) trên đường ray sao cho tiếp tuyến tại hai điểm này có cùng độ dốc (cùng hệ số góc). Đồng thời, đoạn đường nối hai trụ đỡ tại các điểm A và B phải vuông góc với một đường dây điện có phương trình \(x + y - 5 = 0\). Tìm \(b + d\)
Ở trên biển, hai con tàu \(A\) và \(B\) đang ở cùng một vĩ tuyến và cách nhau \(10\) hải lý. Cả hai tàu đồng thời cùng khởi hành. Tàu \(A\) chạy về hướng Nam với vận tốc \(8\) hải lý/giờ, còn tàu \(B\) chạy về vị trí hiện tại của tàu \(A\) với vận tốc \(6\) hải lý/giờ. Hỏi sau bao nhiêu giờ thì khoảng cách giữa hai tàu là ngắn nhất (làm tròn kết quả đến hàng phần mười)?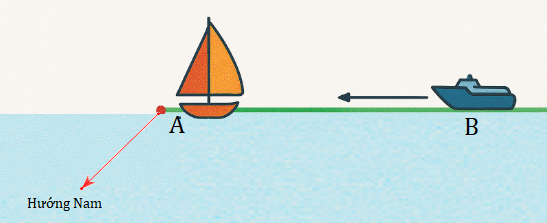
Có ba lực cùng tác động vào một cái bàn như hình vẽ. Trong đó hai lực \(\overrightarrow {{F_1}} ,\,\overrightarrow {{F_2}} \) có giá nằm trên mặt phẳng chứa mặt bàn, tạo với nhau một góc \({110^0}\) và có độ lớn lần lượt là \(9N\) và \(4N\), lực \(\overrightarrow {{F_3}} \) vuông góc với mặt bàn và có độ lớn \(7N\). Độ lớn hợp lực của ba lực trên là \(a\left( N \right)\), tìm giá trị của \(a\). (kết quả quy tròn về số nguyên).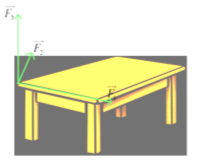
Giả sử doanh số (tính bằng số sản phẩm) của một sản phẩm mới (trong vòng một số năm nhất định) tuân theo quy luật logistic được mô hình hoá bằng hàm số \(f(t) = \frac{{5000}}{{1 + 5{e^{ - t}}}},t \ge 0\) trong đó thời gian \(t\) được tính bằng năm, kể từ khi phát hành sản phẩm mới. Khi đó, đạo hàm \(f\prime (t)\) sẽ biểu thị tốc độ bán hàng. Hỏi sau khi phát hành bao nhiêu năm thì tốc độ bán hàng là lớn nhất? (làm tròn kết quả đến hàng phần mười)
Một vận động viên thể thao hai môn phối hợp luyện tập với một bể bơi hình chữ nhật rộng \(400\;m\), dài \(800\;m\). Vận động viên chạy phối hợp với bơi như sau: Xuất phát từ điểm \(A\), chạy đến điểm \(X\) và bơi từ điểm \(X\) đến điểm \(C\).
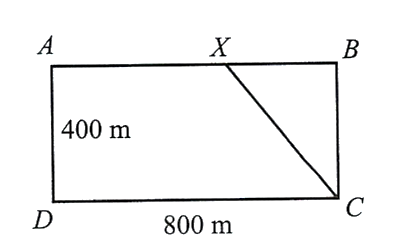
Hỏi nên chọn điểm \(X\) cách \(A\) gần bằng bao nhiêu mét để vận động viên đến \(C\) nhanh nhất ? Biết rằng vận tốc chạy là \(30\;km/h\), vận tốc bơi là \(6\;km/h\).
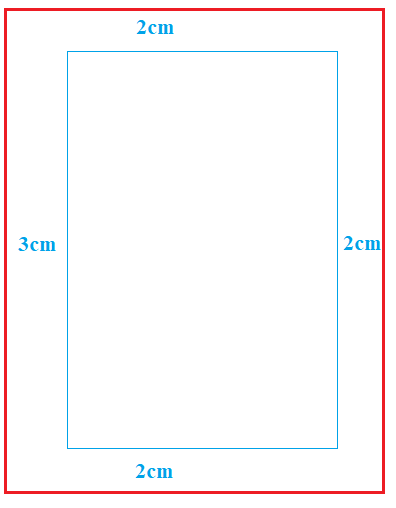
Diện tích một trang của một cuốn sách là \(600c{m^2}\). Do yêu cầu kĩ thuật, cần để lề trên và lề dưới là \(2cm\), lề trái là \(3cm\) và lề phải là \(2cm\). Tính diện tích lớn nhất của phần chữ in vào cuốn sách được (kết quả làm tròn đến hàng đơn vị)
