Bộ 20 đề thi Giữa kì 1 Toán 12 Kết nối tri thức có đáp án - Đề 16
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hàm số \(y = f(x)\) có đồ thị như hình bên. Giá trị lớn nhất của hàm số này trên đoạn \(\left[ { - 1;2} \right]\) bằng
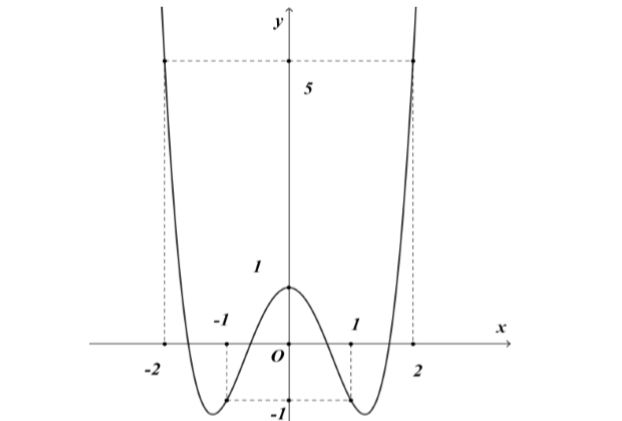
\(2\).
\(5\).
Không xác định.
\(1\).
Trong không gian Oxyz, cho hai điểm \[A\left( {1;3;2} \right)\]và \[B\left( { - 2;3;5} \right)\] tọa độ véctơ \[\,\overrightarrow {BA} \] là
\(\left( { - 3;0;3} \right)\).
\(\,\left( {1;0; - 1} \right)\).
\(\,\left( { - 1;0;1} \right)\).
\(\left( {3;0; - 3} \right)\).
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu \[\left( S \right):{x^2} + {y^2} + {z^2} - 2x + 4y - 4z - 25 = 0\]. Tìm tọa độ tâm \[I\] và bán kính \[R\] của mặt cầu \[\left( S \right)\].
\[I\left( { - 1\,;\, - 2\,;\,2} \right)\]; \[R = 6\].
\[I\left( {1\,;\, - 2\,;\,2} \right)\]; \[R = \sqrt {34} \].
\[I\left( { - 1\,;\,2\,;\, - 2} \right)\]; \[R = 5\].
\[I\left( { - 2;4; - 4} \right)\]; \[R = \sqrt {29} \].
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
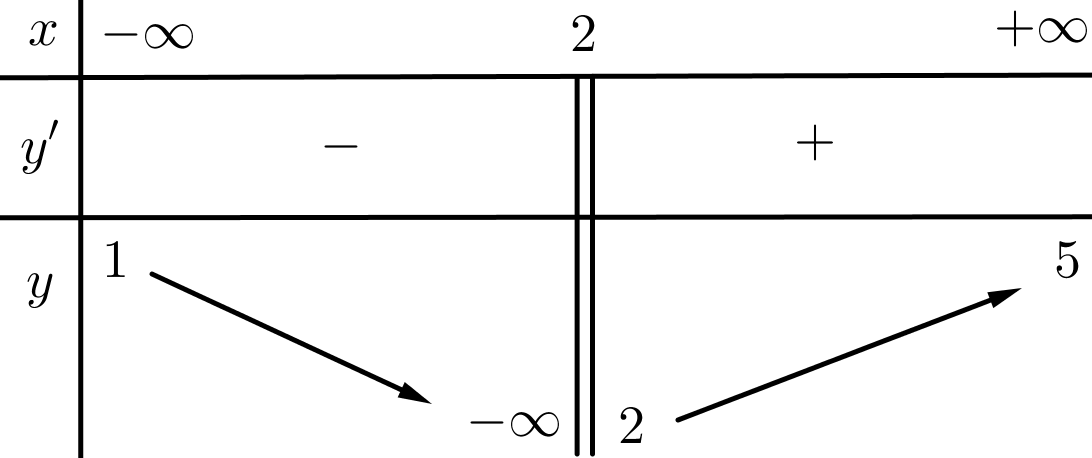
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(y = f\left( x \right)\) là
2.
0.
1.
3.
Hàm số \(y = - {x^4} + 2{x^2} + 1\) đồng biến trên khoảng nào dưới đây?
\(\left( { - \infty ; - 1} \right)\).
\(\left( {0; + \infty } \right)\,.\)
\(\left( { - \infty ;0} \right)\).
\(\left( {1; + \infty } \right)\).
Trong không gian Oxyz, cho hai vectơ \(\overrightarrow a = \left( {2;\;4;\; - 2} \right)\) và \(\overrightarrow b = \left( {1;\; - 2;\;3} \right)\). Tích vô hướng của hai vectơ\(\overrightarrow a \)và \(\overrightarrow b \) bằng
\( - 22\).
\( - 12\).
\(30\).
\(6\).
Cho hình lập phương\[ABCD.{A_1}{B_1}{C_1}{D_1}\]. Gọi O là tâm của hình lập phương. Chọn đẳng thức đúng?
\[\overrightarrow {AO} = \frac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {A{A_1}} } \right)\].
\[\overrightarrow {AO} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {A{A_1}} } \right)\].
\[\overrightarrow {AO} = \frac{2}{3}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {A{A_1}} } \right)\].
Cho hàm số \(y = f\left( x \right)\)có đạo hàm là \(f'\left( x \right) = x{\left( {x + 1} \right)^2}\left( {x - 1} \right)\). Hàm số \(y = f\left( x \right)\)có bao nhiêu điểm cực trị?
\[0\].
\[2\].
\(3\).
\[1\].
Trong không gian Oxyz cho ba điểm: \(A\left( {1; - 1;1} \right),\)\(B\left( {0;1;2} \right),\)\(C\left( {1;0;1} \right).\) Trong các mệnh đề sau hãy chọn mệnh đề đúng?
\(B\) là trung điểm của \(AC.\)
Ba điểm \(A\), \(B\), \(C\) không thẳng hàng.
Ba điểm \(A\), \(B\), \(C\) thẳng hàng.
Tam giác \(ABC\) vuông tại \(A.\)
Bảng biến thiên sau là bảng biến thiên của hàm số nào sau đây ?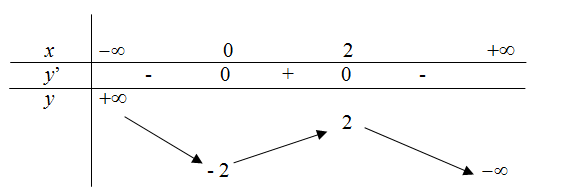
\(y = - {x^3} + 3{x^2} - 2\).
\(y = - {x^3} - 3x - 2\).
\(y = {x^3} - 3{x^2} - 1\).
\(y = - {x^3} + 3{x^2} - 1\).
Tìm tất cả các giá trị thực của tham số \(m\)để giá trị lớn nhất của hàm số \(y = \frac{{x + {m^2}}}{{x - 1}}\)trên \(\left[ {2;4} \right]\)bằng \(2\).
\(m = - 4\).
\(m = - 2\).
\(m = 0\).
\(m = 2\).
Trên đồ thị hàm số \(y = \frac{{2x - 1}}{{x + 4}}\) có bao nhiêu điểm có tọa độ nguyên?
\(4.\)
\(6.\)
\(0.\)
\(2.\)
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Trong không gian Oxyz, cho hai điểm \(M\left( {2;3; - 1} \right),N\left( { - 1;1;1} \right)\).
a) Điểm \(I\left( {a;b;c} \right)\) nằm trên mặt phẳng \(\left( {Oxy} \right)\) thỏa mãn \(T = \left| {3\overrightarrow {IM} - \overrightarrow {IN} } \right|\) đạt giá trị nhỏ nhất. Khi đó \(2a + b + c = 9\).
b) Gọi \(E\) là điểm đối xứng của điểm \(M\) qua \(N\). Tọa độ của điểm \(E\) là \(\left( { - 4; - 1;3} \right)\).
c) Hình chiếu của điểm \(M\) trên trục \(Oy\) có tọa độ là \(\left( { - 2;3;1} \right)\).
d) Cho \(P\left( {1;m - 1;3} \right)\). Tam giác \(MNP\) vuông tại \(N\) khi và chỉ khi \(m = 1\).
Cho hàm số \(y = \frac{{ - {x^2} - 3x + 4}}{{x - 3}}\) có đồ thị là \(\left( C \right)\). Xét tính đúng sai của các khẳng định sau:
a) Đồ thị \(\left( C \right)\) nhận giao điểm \(I\left( {3\,;\, - 9} \right)\) làm tâm đối xứng.
b) Đồ thị \(\left( C \right)\) có tiệm cận xiên là \(y = - x - 6\).
c) Đồ thị không cắt trục \(Ox\).
d) Đồ thị \(\left( C \right)\) có hai điểm cực trị nằm 2 phía đối với \(Oy\).
Nồng độ thuốc \(C\left( t \right)\) tính theo \({\rm{mg}}/{\rm{c}}{{\rm{m}}^3}\)trong máu của bệnh nhân được cho bởi công thức \(C\left( t \right) = \frac{{0,05t}}{{{t^2} + t + 1}}\), trong đó \(t\) là thời gian tính theo giờ kể từ khi tiêm cho bệnh nhân.
Khi đó:
a) Hàm số \(C\left( t \right)\) có đạo hàm \[C'\left( t \right) = \frac{{1 - {t^2}}}{{20{{\left( {{t^2} + t + 1} \right)}^2}}},t \ge 0\].
b) Sau khi tiêm, nồng độ thuốc trong máu bệnh nhân giảm dần theo thời gian.
c) Nồng độ thuốc trong máu bệnh nhân lớn nhất ở thời điểm \(1\) giờ sau khi tiêm.
d) Có thời điểm nồng độ trong máu của bệnh nhân đạt \({\rm{0,02 mg}}/{\rm{c}}{{\rm{m}}^3}\).
Cho hàm số \(y = {x^3} - 3{x^2} + 2\).
a) Đạo hàm của hàm số đã cho là \(y' = 3{x^2} - 6x\).
b) Hàm số đã cho đồng biến trên khoảng \(\left( {0;2} \right)\) và nghịch biến trên các khoảng \(\left( { - \infty ;0} \right),\left( {2; + \infty } \right)\).
c) Bảng biến thiên của hàm số đã cho là:
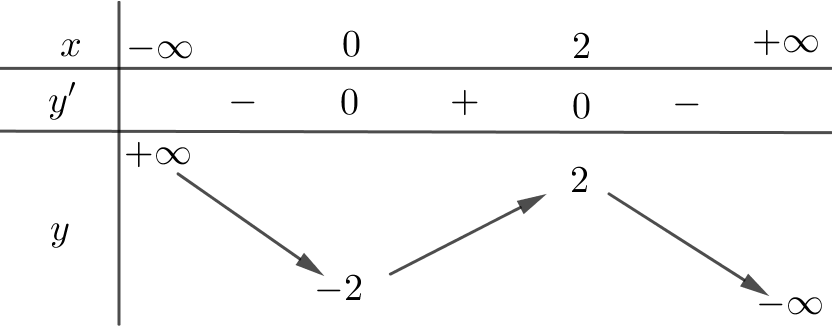
d) Đồ thị của hàm số đã cho như ở hình sau: 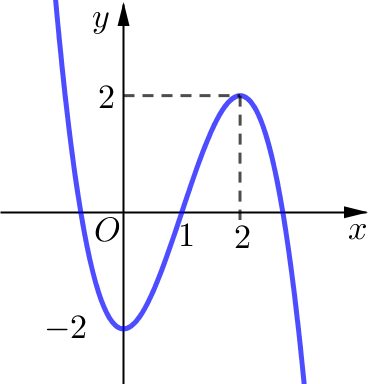
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Một cửa hàng kinh doanh trung bình bán được 700 máy điều hòa mỗi tháng với giá 15 triệu đồng một máy. Một cuộc khảo sát thị trường chỉ ra rằng nếu cứ giảm giá bán 1 triệu đồng, số lượng máy điều hòa bán ra sẽ tăng thêm khoảng 100 máy mỗi tháng. Biết hàm chi phí hàng tháng là \(C\left( x \right) = 14000 - 3x\) (triệu đồng), trong đó \(x\) là số máy điều hòa bán ra trong tháng, cửa hàng nên đặt giá bán bao nhiêu để lợi nhuận là lớn nhất? (đơn vị là triệu đồng).
Trượt nước là một trò chơi vận động được nhiều người yêu thích trong các công viên nước. Một cái máng trượt nước có thiết kế dạng cung tròn với hai đầu mút là \(A\) và \(B\). Chọn hệ trục tọa độ \(Oxyz\) với gốc \(O\) đặt tại hình chiếu của \(A\) trên mặt đất, mặt phẳng \(\left( {Oxy} \right)\) trùng với mặt đất và trục \(Oz\) hướng thẳng đứng lên trời, đơn vị đo lấy theo mét (tham khảo hình vẽ dưới đây). Biết các điểm \(A,B\) và một điểm \(C\)nằm trên máng trượt lần lượt có tọa độ là \(\left( {0;0;5} \right),\left( {6;7;1} \right)\) và \(\left( {5;0;2} \right)\). Độ dài máng trượt nước đó bằng bao nhiêu mét (làm tròn kết quả đến hàng đơn vị của mét)?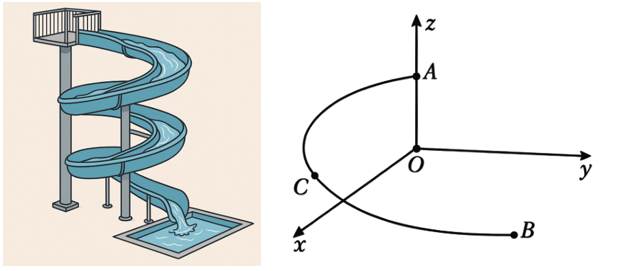
Nhà máy \(A\) chuyên sản xuất một loại sản phẩm cung cấp cho nhà máy \(B\). Hai nhà máy thỏa thuận rằng, hàng tháng nhà máy \(A\) cung cấp cho nhà máy \(B\) số lượng sản phẩm theo đơn đặt hàng của \(B\) (tối đa \(100\) tấn sản phẩm). Nếu số lượng đặt hàng là \(x\) tấn sản phẩm thì giá bán cho mỗi tấn sản phẩm là \(P\left( x \right) = 45 - 0,001{x^2}\) (triệu đồng). Chi phí để \(A\) sản xuất \(x\) tấn sản phẩm trong một tháng là \(C\left( x \right) = 100 + 30x\) (triệu đồng) (gồm \(100\) triệu đồng chi phí cố định và \(30\) triệu đồng cho mỗi tấn sản phẩm). Để mỗi tháng thu được lợi nhuận lớn nhất thì \(A\) cần bán cho \(B\) bao nhiêu tấn sản phẩm mỗi tháng để lợi nhuận thu được là lớn nhất? (kết quả làm tròn đến hàng đơn vị)
Một chất điểm A nằm trên mặt phẳng nắm ngang (a), chịu tác động bởi ba lực F1, F2, F3. Các lực F, F2 có giá nằm trong (a) và (F1; F2) =135°, còn lực Fs có giá vuông góc với (a) và hướng lên trên. Độ lớn hợp lực của các lực F1, F2, F3 bằng bao nhiêu Niu-tơn, biết rằng độ lớn của ba lực đó lần lượt là 20N, 15N và 10N (làm tròn kết quả đến hàng phần chục)?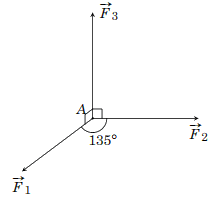
Khi chất thải hữu cơ được đổ vào một cái ao, quá trình ôxy hóa xảy ra sẽ làm giảm hàm lượng ôxy trong nước. Tuy nhiên, theo thời gian, tự nhiên sẽ phục hồi lại mức ôxy về giá trị bình thường. Trong đồ thị kèm theo, \(P(t)\) cho biết phần trăm hàm lượng ôxy (so với mức bình thường) sau \(t\) ngày kể từ khi chất thải được đổ vào ao.
Giả sử hàm số cho hàm lượng ôxy là \(P(t) = 100\frac{{{t^2} + 10t + 100}}{{{t^2} + 20t + 100}}\)(\(\% \)mức bình thường), \({\rm{t}} \ge {\rm{0}}{\rm{. }}\)
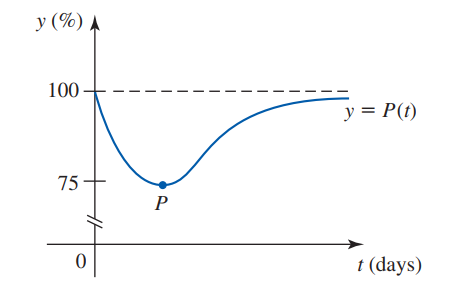
Khi đó tọa độ của điểm \(P\left( {a;b} \right)\) trên đồ thị là điểm cực trị của đồ thị hàm số \(P(t)\). Tính \(a + b\)?
Xí nghiệp \(A\) sản xuất độc quyền một loại sản phẩm. Biết rằng hàm tổng chi phí sản xuất là \(TC = {x^3} - 77{x^2} + 1000x + 40000\) và hàm doanh thu là \(TR = - 2{x^2} + 1312x\), với \(x\) là số sản phẩm. Lợi nhuận của xí nghiệp \(A\) được xác định bằng hàm số \(f\left( x \right) = TR - TC\), cực đại lợi nhuận của xí nghiệp \(A\) khi đó đạt bao nhiêu sản phẩm?








