Bộ 20 đề thi Giữa kì 1 Toán 12 Kết nối tri thức có đáp án - Đề 20
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Trong không gian Oxyz, hình chiếu vuông góc của điểm \(M\left( {4; - 1;3} \right)\)trên mặt phẳng \[\left( {Oyz} \right)\]có tọa độ là:
\(\left( { - 1;3;0} \right).\)
\(\left( {0; - 1;0} \right).\)
\(\left( {0; - 1;3} \right).\)
\(\left( {4;0;0} \right).\)
Trong không gian Oxyz cho hai vectơ \(\overrightarrow a = (1; - 1;2)\) và \(\overrightarrow b = (2;1; - 1)\). Tính \(\overrightarrow a .\overrightarrow b \).
\(\overrightarrow a .\overrightarrow b = 1\).
\(\overrightarrow a .\overrightarrow b = (2; - 1; - 2)\).
\(\overrightarrow a .\overrightarrow b = ( - 1;5;3)\).
\(\overrightarrow a .\overrightarrow b = - 1\).
Cho hàm số \(y = f(x)\) có bảng biến thiên như hình vẽ. Phương trình các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là
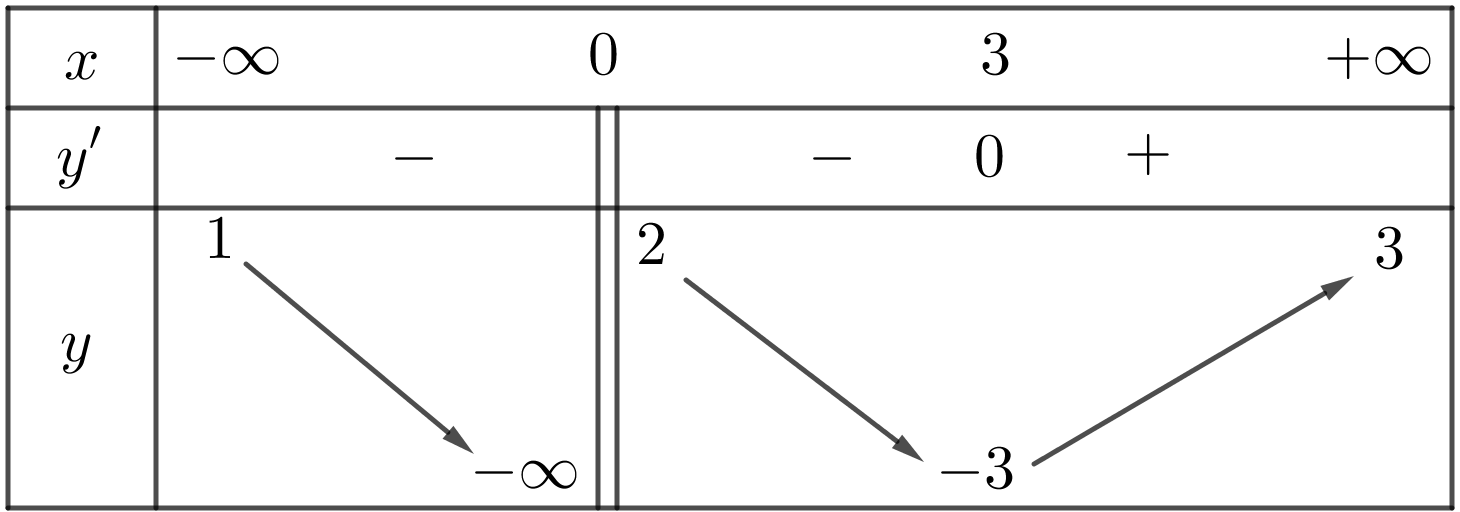
\(y = 0\);\(x = 1\);\(x = 3\).
\(x = 0\);\(y = 1\) .
\(y = 0\);\(x = 1\) .
\(x = 0\);\(y = 1\);\(y = 3\) .
Trong không gian với hệ tọa độ Oxyz, tính bán kính \(R\) của mặt cầu \(\left( S \right):\,{x^2} + {y^2} + {z^2} - 2x - 4y = 0\)
\(\sqrt 5 \).
\(2\).
\(\,5\).
\(\sqrt 6 \).
Cho hàm số \(y = f\left( x \right)\) xác định trên nửa khoảng \(\left[ { - 1;3} \right)\) có bảng biến thiên như hình vẽ.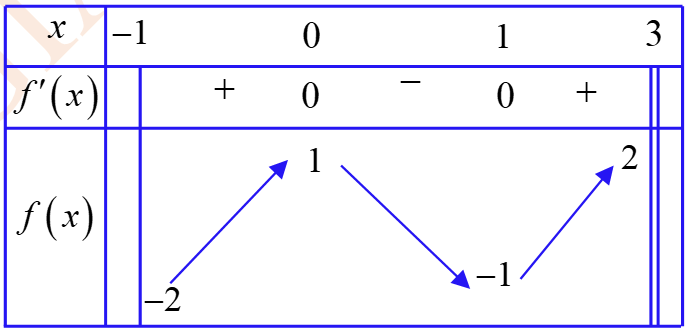
Khẳng định nào sau đây đúng?
\(\mathop {{\rm{max}}}\limits_{x \in \left[ { - 1;3} \right)} f\left( x \right) = 1\).
\(\mathop {{\rm{max}}}\limits_{x \in \left[ { - 1;3} \right)} f\left( x \right) = 2\).
\(\mathop {{\rm{min}}}\limits_{x \in \left[ { - 1;3} \right)} f\left( x \right) = - 2\).
\(\mathop {{\rm{min}}}\limits_{x \in \left[ { - 1;3} \right)} f\left( x \right) = - 1\).
Cho hàm số \(y = - {x^3} + 3{x^2} - 3x + 2\). Khẳng định nào sau đây là khẳng định đúng?
Hàm số đồng biến trên \[\mathbb{R}\].
Hàm số nghịch biến trên \[\mathbb{R}\].
Hàm số đồng biến trên khoảng \(\left( { - \infty ;1} \right)\) và nghịch biến trên khoảng \(\left( {1; + \infty } \right)\).
Hàm số nghịch biến trên khoảng \(\left( { - \infty ;1} \right)\) và đồng biến trên khoảng \(\left( {1; + \infty } \right)\).
Cho hình lăng trụ ABC.A'B'C', \(K\) là trung điểm của \(BB'\). Đặt \(\overrightarrow {CA} = \overrightarrow a ,\,\overrightarrow {CB} = \overrightarrow b ,\,\overrightarrow {AA'} = \overrightarrow c \). Khẳng định nào sau đây đúng?
\(\overrightarrow {AK} = \overrightarrow { - a} + \overrightarrow b + \frac{1}{2}\overrightarrow c \).
\(\overrightarrow {AK} = \overrightarrow a - \frac{1}{2}\overrightarrow b + \overrightarrow c \).
\(\overrightarrow {AK} = - \frac{1}{2}\overrightarrow a + \overrightarrow b + \overrightarrow c \).
\(\overrightarrow {AK} = \overrightarrow a + \frac{1}{2}\overrightarrow b - \overrightarrow c \).
Biết rằng bảng biến thiên sau là bảng biến thiên của một hàm số trong các hàm số được liệt kê ở các phương án \[A,B,C,D\] dưới đây. Hỏi hàm số đó là hàm số nào?
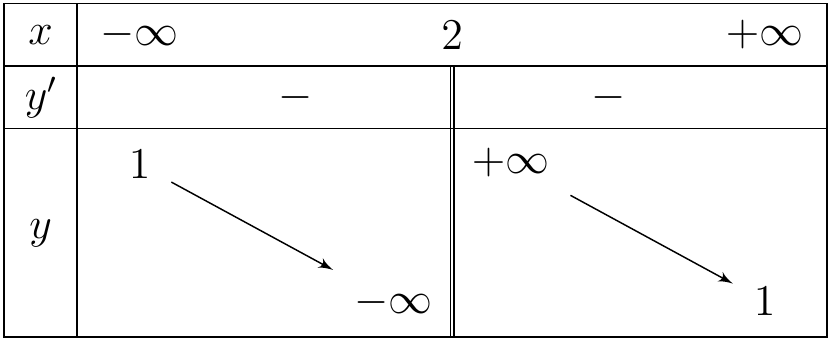
\(y = \frac{{x + 1}}{{x - 2}}\).
\(y = \frac{{2x - 1}}{{x + 2}}\).
\(y = \frac{{2x + 5}}{{x + 2}}\).
\(y = \frac{{x - 3}}{{x - 2}}\).
Cho hàm số có đồ thị như hình bên dưới.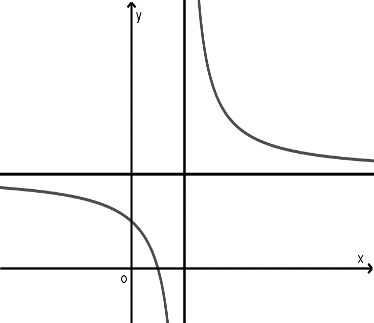
Mệnh đề nào dưới đây đúng?
\[\left\{ {\begin{array}{*{20}{c}}{a < 0}\\{d < 0}\end{array}} \right.\]
\[\left\{ {\begin{array}{*{20}{c}}{a < 0}\\{d > 0}\end{array}} \right.\]
\[\left\{ {\begin{array}{*{20}{c}}{a > 0}\\{d < 0}\end{array}} \right.\]
\[\left\{ {\begin{array}{*{20}{c}}{a > 0}\\{d > 0}\end{array}} \right.\]
Trong không gian với hệ trục tọa độ Oxyz cho ba điểm \(A\left( {3; - 2;3} \right),B\left( { - 1;2;5} \right),C\left( {1;0;1} \right)\) . Tìm tọa độ trọng tâm \(G\) của tam giác \(ABC\).
\(G\left( { - 1;0;3} \right)\).
\(G\left( {1;0;3} \right)\).
\(G\left( {0;0; - 1} \right)\).
\(G\left( {3;0; - 1} \right)\).
Để giá trị nhỏ nhất của hàm số \(y = x + \frac{1}{x} - m\)trên khoảng \(\left( {0; + \infty } \right)\)bằng \( - 3\)thì giá trị của tham số \(m\)là:
\(m = \frac{{19}}{3}\).
\(m = 5\).
\(m = \frac{{11}}{2}\).
\(m = 7\).
Cho hàm số \[f\left( x \right)\]có đạo hàm \[f'\left( x \right) = x{\left( {x + 1} \right)^2}{\left( {x - 2} \right)^4},\forall x \in \mathbb{R}\]. Tìm số điểm cực trị của hàm số \[y = f\left( x \right).\]
\(2.\)
\(3.\)
\(0.\)
\(1.\)
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Một chất điểm chuyển động theo phương trình \[s(t) = {t^3} - 3{t^2} + 8t + 1\], trong đó \[t\] tính bằng giây và \[s(t)\] tính bằng mét.
a) Vận tốc của chất điểm tại thời điểm \[t = 3\left( s \right)\] bằng \[8\,\,m/s\].
b) Tại thời điểm mà chất điểm di chuyển được \[13m\], vận tốc khi đó bằng \[8\,\,m/s\].
c) Vận tốc nhỏ nhất của chất điểm là \[5\,m/s\].
d) Gia tốc tại thời điểm chất điểm đạt vận tốc nhỏ nhất bằng \[2\,m/{s^2}\].
Trong hệ trục Oxyz, cho 3 điểm \(A(1;0;0),B(0;0;1),C(2;1;1)\). Xét tính đúng sai của các mệnh đề sau:
a) Diện tích của tam giác \(ABC\) bằng \(\frac{{\sqrt 6 }}{2}\)
b) Độ dài đường cao của tam giác \(ABC\) hạ từ \(A\) bằng \(AH = \frac{{\sqrt {30} }}{5}\)
c) Gọi \(D(x;y;z)\) sao cho tứ giác \(ABCD\) là một hình bình hành khi đó \(x + y + z = 3\)
d) Thể tích của khối chóp \(SABCD\) với đỉnh \(S(0;3;4)\) bằng \(2\)
Cho hàm số \(y = \frac{{ - {x^2} + 2\left( {m + 1} \right)x - 5}}{{x - 1}}\)có đồ thị \(\left( C \right)\) với \(m\) là tham số
a) Khi \(m = 0\) thì đồ thị hàm số có tiệm cận xiên là \(y = - x + 1\)
b) Khi \(m = 0\) thì đồ thị hàm số không cắt \(Ox\).
c) Để hàm số có cực đại và cực tiểu thì \(m > 4\)
d) Tồn tại 1 điểm \(M\) thuộc đồ thị \(\left( C \right)\) sao cho \({x_M} > 1\) và độ dài \(IM\) ngắn nhất (\[I\] là tâm đối xứng của \(\left( C \right)\)) khi đó tung độ \({y_M} < - 4\).
Cho hàm số \(y = \frac{1}{3}{x^3} - m{x^2} + \left( {m + 1} \right)x - 1\) (\(m\) là tham số). Khi đó:
a) Với \(m = - 1\) thì hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right)\)
b) Với \(m = - 1\) thì đồ thị hàm số có một điểm cực tiểu là \(\left( {0;2} \right)\)
c) Ta có \(y' = {x^2} - 2mx + m + 1\).
d) Để hàm số \(y = \frac{1}{3}{x^3} - m{x^2} + \left( {m + 1} \right)x - 1\) đạt cực đại tại \(x = - 2\) thì \(m = k\), khi đó phương trình \({2^{x + k}} = 4\) có nghiệm là \(x = 3\)
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
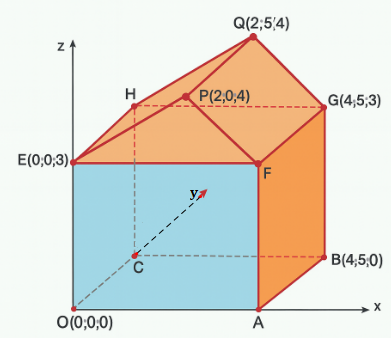
Hình bên dưới minh họa sơ đồ một ngôi nhà trong không gian \(Oxyz\), trong đó nền nhà, bốn bức tường và hai mái nhà đều là hình chữ nhật. Tính số đo góc dốc của mái nhà, tức là số đo của góc nhị diện có cạnh là đường thẳng \[FG\], hai mặt \(\left( {FGQP} \right)\) và \(\left( {FGHE} \right)\).
Một tẩm gỗ tròn được treo song song với mặt phẳng nằm ngang bởi ba sợi dây không dãn xuất phát từ điểm O trên trần nhà và lần lượt buộc vào ba điểm A, B,C trên tấm gỗ tròn sao cho các lực căng F1, F2, F3 lần lượt trên mỗi dây OA,OB,OC đôi một vuông góc với nhau và có độ lớn Fl = F2 = F3 =20( N) . Trọng lượng P của tấm gỗ tròn đó bằng bao nhiêu Niu-tơn ?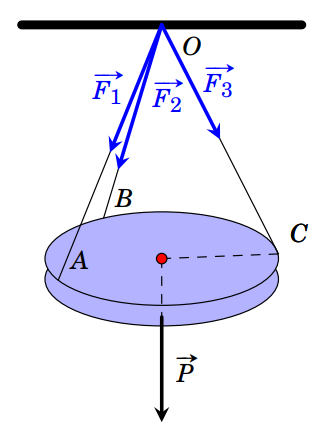
Một vật chuyển động theo quy luật \(S = - {t^3} + 18{t^2}\), với \(t\) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và \(s\) là quãng đường vật đi được trong thời gian đó. Hỏi trong khoảng thời gian 10 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu ?
Một người có một dây ruy băng dài 130 cm, người đó dùng dải ruy băng này để trang trí hộp quà hình trụ. Khi trang trí hộp quà, người này dùng 10cm của dải ruy băng để thắt nơ ở trên nắp hộp . Với dải ruy băng có kích thước như trên có thể trang trí được hộp quà có thể tích lớn nhất là bao nhiêu \(d{m^3}\)?
Trong thống kê tại một chuỗi nhà máy của công ty X, nếu áp dụng tuần làm việc 40 giờ thì mỗi tuần có 100 tổ công nhân đi làm và mỗi tổ làm được 120 sản phẩm trong một giờ. Nếu tăng thời gian làm việc thêm 2 giờ mỗi tuần sẽ có thêm 1 tổ nghỉ việc và năng suất lao động giảm 5 sản phẩm/1 tổ/1 giờ . Ngoài ra, số phế phẩm mỗi tuần ước tính là \(P\left( x \right) = \frac{{95{x^2} + 120x}}{4}\), với \(x\) là thời gian làm việc trong một tuần. Công ty cần áp dụng thời gian làm việc mấy giờ mỗi tuần để số lượng sản phẩm thu được hàng tuần là lớn nhất?
Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ \(t\) là \(N(t) = 45{t^2} - {t^3},0 \le t \le 30\) . Nếu xem \({N^\prime }(t)\) là tốc độ truyền bệnh tại thời điểm \(t\) thì tốc độ truyền bệnh lớn nhất sẽ vào ngày thứ bao nhiêu?








