Bộ 20 đề thi Giữa kì 1 Toán 12 Kết nối tri thức có đáp án - Đề 12
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Hàm số \(y = \frac{1}{x}\) nghịch biến trên khoảng
\(\left( {0; + \infty } \right).\)
\(\left( { - \infty ; + \infty } \right).\)
\(\left( { - \infty ;1} \right).\)
\(\left( { - 1; + \infty } \right).\)
Trong không gian với hệ trục toạ độ Oxyz, mặt cầu \(\left( S \right)\,\,:\,{\left( {x + 2} \right)^2} + {\left( {y - 1} \right)^2} + {z^2} = 4\) có tâm \(I\) và bán kính \(R\) lần lượt là
\(I\left( {2; - 1;0} \right);R = 4\).
\(I\left( { - 2;1;0} \right);R = 2\).
\(I\left( {2; - 1;0} \right);R = 2\).
\(I\left( { - 2;1;0} \right);R = 4\).
Trong không gian Oxyz, cho hai điểm \(A\left( { - 1;\,2;\,4} \right)\) và \(B\left( {3;\,0;\, - 2} \right)\). Trung điểm của đoạn thẳng \(AB\) có tọa độ là :
\(\left( { - 2;\,1;\,3} \right).\)
\(\left( {2;\, - 1;\, - 3} \right).\)
\(\left( {4;\, - 2;\, - 6} \right).\)
\(\left( {1;\,1;\,1} \right).\)
Trong không gian cho hai điểm \(A\left( { - 1\,;\,2\,;\,3} \right)\), \(B\left( {0\,;1\,;1} \right)\) độ dài đoạn \(AB\) bằng
\(\sqrt 8 \).
\(\sqrt {10} \).
\(\sqrt {12} \).
\(\sqrt 6 \).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên dưới đây: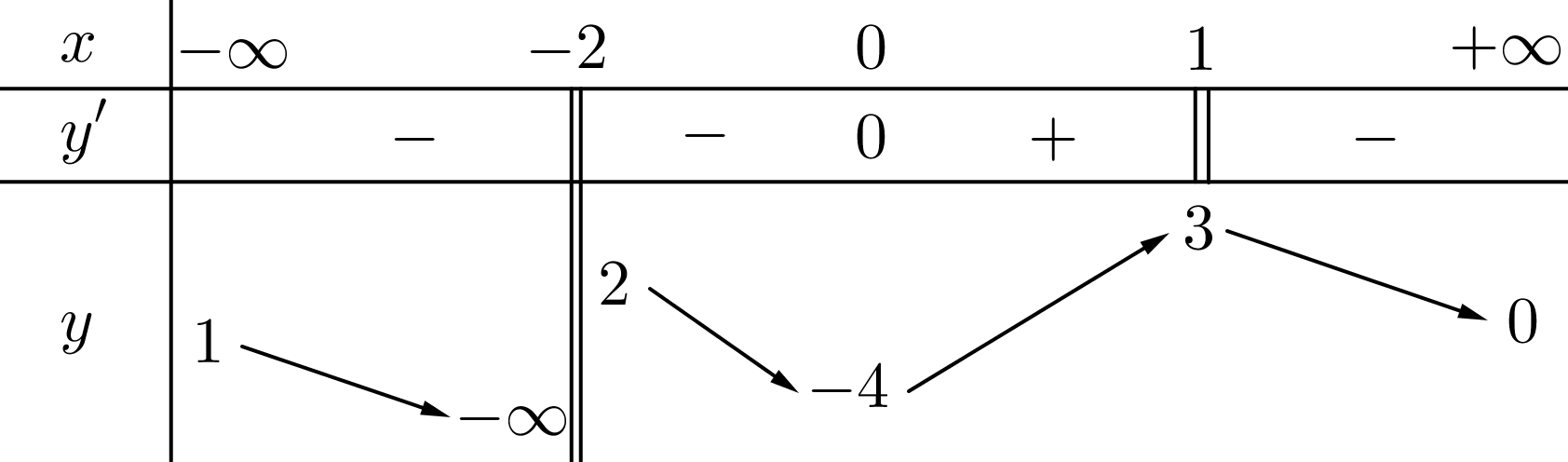
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(y = f\left( x \right)\) là
\(2\).
\(4\).
\(1\).
\(3\).
Hàm số \(y = f(x)\) liên tục trên \(\left[ { - 1;3} \right]\) có bảng biến thiên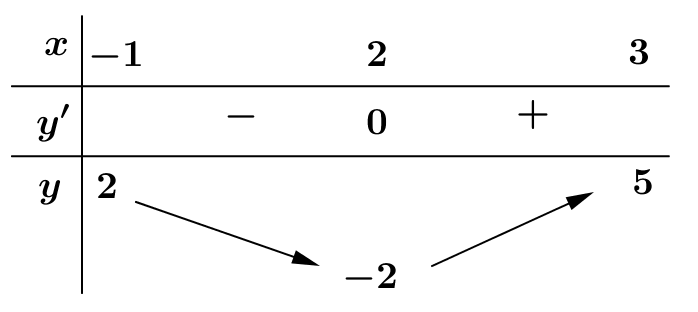
Giá trị nhỏ nhất của hàm số trên đoạn \(\left[ { - 1;3} \right]\) là
1.
-2.
0.
2.
Tìm giá trị của \(m\) để hàm số \(y = - {x^3} + 3{x^2} + m + 1\) có giá trị nhỏ nhất trên đoạn \(\left[ { - 2;1} \right]\) bằng 4 là
\(m = 1\).
\(m = 3\).
\(m = 4\).
\(m = - 17\).
Bảng biến thiên ở trong hình vẽ là của hàm số nào dưới đây?
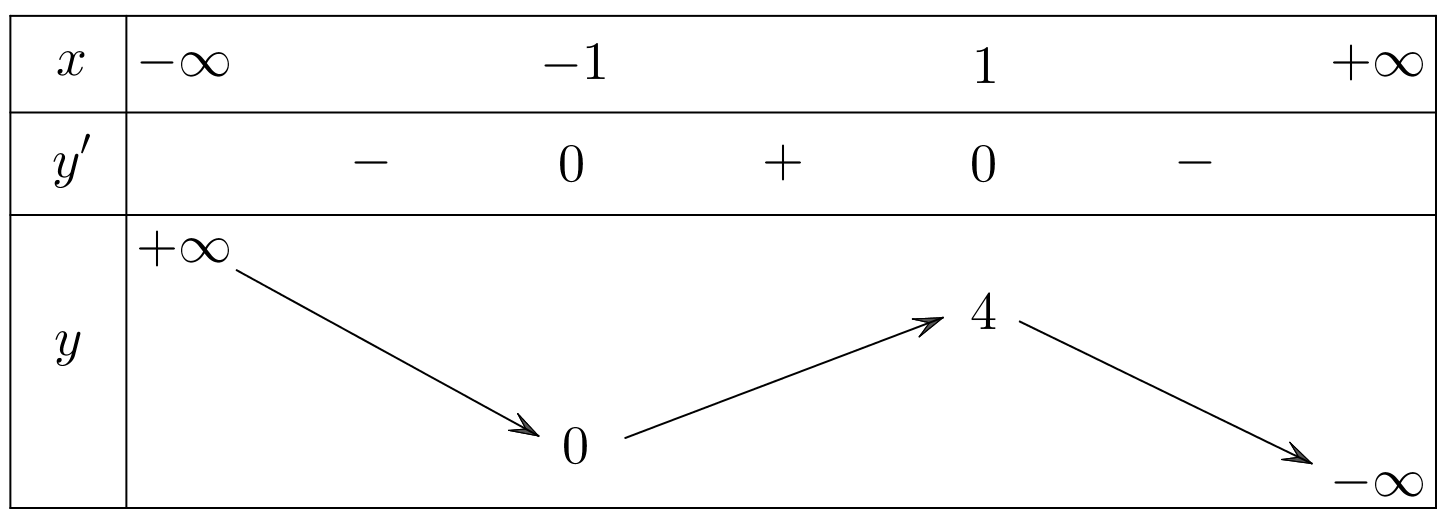
\(y = {x^4} - 2{x^2} - 3\).
\(y = {x^3} - 3x + 4\).
\(y = - {x^3} - 3x + 2\).
\(y = - {x^3} + 3x + 2\).
Cho hàm số \[y = a{x^4} + b{x^2} + c\,\,\left( {a,b,c \in \mathbb{R}} \right)\] có đồ thị như hình bên dưới. Mệnh đề nào dưới đây đúng?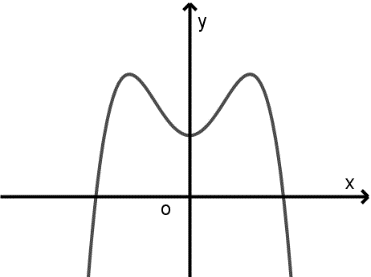
\[a > 0;\,b > 0;c < 0.\]
\[a < 0;\,b > 0;c > 0.\]
\[a > 0;\,b < 0;c < 0.\]
\[a < 0;\,b < 0;c > 0.\]
Trong không gian với hệ tọa độ Oxyz, cho bốn điểm \(A\left( {1;\,0;\,2} \right)\), \(B\left( { - 2;\,1;\,3} \right)\), \(C\left( {3;\,2;\,4} \right)\), \(D\left( {6;\,9;\, - 5} \right)\). Hãy tìm tọa độ trọng tâm của tứ diện \(ABCD\)?
\(\left( {2;\,3;\, - 1} \right)\).
\(\left( {2;\, - 3;\,1} \right)\).
Cho hàm số \(f\left( x \right)\)có đạo hàm \(f'\left( x \right) = \left( {x + 1} \right){\left( {{x^2} - 1} \right)^3}\left( {x + 2} \right),\forall x \in \mathbb{R}\). Số điểm cực trị của hàm số đã cho là:
1.
3.
2.
5.
Cho hình lăng trụ ABC.A'B'C' với \(G\) là trọng tâm của tam giác \(A'B'C'.\) Đặt \[\overrightarrow {AA'} = \overrightarrow a \], \[\overrightarrow {AB} = \overrightarrow b \], \[\overrightarrow {AC} = \overrightarrow c \]. Khi đó \(\overrightarrow {AG} \)bằng:
\(\overrightarrow a + \frac{1}{4}\left( {\overrightarrow b + \overrightarrow c } \right).\;\)
\(\overrightarrow a + \frac{1}{6}\left( {\overrightarrow b + \overrightarrow c } \right).\)
\(\overrightarrow a + \frac{1}{2}\left( {\overrightarrow b + \overrightarrow c } \right).\)
\(\overrightarrow a + \frac{1}{3}\left( {\overrightarrow b + \overrightarrow c } \right).\)
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(y = \frac{{ - {x^2} - 3x + 4}}{{x - 3}}\) có đồ thị là \(\left( C \right)\).
a) Đồ thị \(\left( C \right)\) có tiệm cận xiên là \(y = - x - 6\).
b) Đồ thị \(\left( C \right)\) nhận giao điểm \(I\left( {3; - 9} \right)\) làm tâm đối xứng.
c) Đồ thị không cắt trục \(Ox\).
d) Đồ thị \(\left( C \right)\) có hai điểm cực trị nằm 2 phía đối với \(Oy\).
Cho một tấm nhôm hình vuông cạnh \(2016\left( {cm} \right)\). Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng \[x\left( {cm} \right)\], rồi gập tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Hỏi:
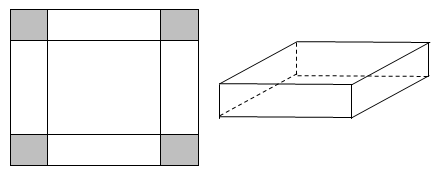
a) Để hộp nhận được có thể tích lớn nhất thì \[x = 250\left( {cm} \right)\].
b) Để hộp nhận được có thể tích lớn nhất thì \[x = 336\left( {cm} \right)\].
c) Hộp nhận được có thể tích lớn nhất là \[606928896\left( {c{m^3}} \right)\].
d) Hộp nhận được có thể tích lớn nhất là \[606928000\left( {c{m^3}} \right)\].
Cho hàm số \(y = {x^3} - m{x^2} - \left( {m - 6} \right)x + 1\)(tham số \[m\]). Khi đó:
a) Để hàm số đồng biến trên khoảng \(\left( {0;4} \right)\) thì \(m \le 2\)
b) Với \(m = 6\) thì hàm số đồng biến trên khoảng \(\left( {4; + \infty } \right)\)
c) Với \(m = 0\) thì hàm số nghịch biến trên khoảng \(\left( { - \infty ; + \infty } \right)\)
d) Tập hợp tất cả các giá trị của tham số\(m\) để hàm số đồng biến trên khoảng \(\left( {0;4} \right)\) là \(\left( { - \infty ;a} \right]\). Khi đó \(\mathop {\lim }\limits_{x \to a} \left( {x + 2024} \right) = 2027\)
Trong không gian với hệ tọa độ Oxyz, cho các điểm \(A\left( {2;\,1;\, - 1} \right)\), \(B\left( {3;\,1;\,0} \right)\), \(C\left( { - 1;\,1;\,3} \right)\). Các mệnh đề sau đúng hay sai?
a) Ba điểm \(A,\,B,\,D\left( {4;1;1} \right)\)thẳng hàng.
b) Góc \(\widehat {ABC} = 45^\circ \).
c) Ba điểm \(A,\,B,\,C\)không thẳng hàng.
d) \(\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {0; - 7;0} \right)\).
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Từ một tấm bìa mỏng hình vuông cạnh 6 \(dm\), bạn Hoa cắt bỏ bốn tam giác cân bằng nhau có cạnh đáy là cạnh của hình vuông ban đầu và đỉnh là đỉnh của một hình vuông nhỏ phía trong rồi gập lên, ghép lại tạo thành một khối chóp tứ giác đều. Thể tích của khối chóp có giá trị lớn nhất bằng bao nhiêu decimét khối ?
Hàm chi phí của một nhà máy được cho bởi \(C = C(Q) = \frac{{{Q^2}}}{4} + 3Q + 400\) trong đó \(C\) là tổng chi phí sản xuất \(Q\) đơn vị sản phẩm. Với mức sản lượng là bao nhiêu thì chi phí trung bình tính trên mỗi đơn vị sản phẩm là thấp nhất? Khi đó chi phí trung bình tối thiểu bằng bao nhiêu?
Một ngôi nhà gồm hai phần. Phần thân nhà dạng hình hộp chữ nhật ABCD.OMNK có chiều dài \(1200cm\), chiều rộng \(900cm\), chiều cao\(450cm\). Phần mái nhà dạng hình chóp\(S.ABCD\) có các cạnh bên bằng nhau và tạo với mặt đáy góc \(\alpha \)với \(\tan \alpha = \frac{1}{5}\). Chọn hệ trục toạ độ \(Oxyz\)sao cho \(M\)thuộc tia \(Ox,\)\(K\)thuộc tia \(Oy,\)\(A\)thuộc tia \(Oz\)(như hình vẽ). Biết \(S\left( {a;b;c} \right)\) (đơn vị của \(a,b,c\)là centimet). Tính giá trị của biểu thức \(P = a + b + c.\)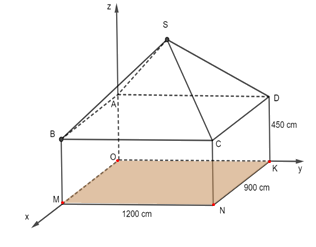
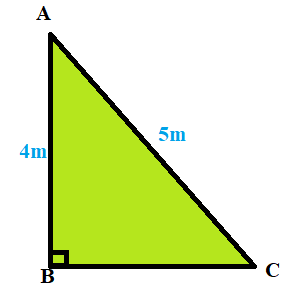
Chào đón năm mới \(2025\), Thành phố trang trí đèn led biểu tượng hình chữ \(V\) được ghép từ các thanh \(AB = 4m\), \(AC = 5m\) sao cho tam giác \(ABC\) vuông tại \(B\). Để tăng hiệu ứng, các kỹ sư đã thiết kế một chuỗi led chạy từ \(B\) xuống \(A\) với vận tốc \(4\)\({\rm{m/}}\)phút và một chuỗi led chạy từ \(A\) lên \(C\) với vận tốc \(10\)\({\rm{m/}}\)phút. Sau khi đóng nguồn điện thì cả hai chuỗi led đồng thời xuất phát. Hỏi sau bao nhiêu giây từ thời điểm đóng nguồn thì khoảng cách giữa hai điểm sáng đầu tiên của hai chuỗi led là nhỏ nhất ?
Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể trong \(t\) giờ được tính theo công thức \(g\left( t \right) = \frac{{ - {t^2} + 5t - 3}}{{t + 1}}\). Sau khi tiêm thuốc bao lâu thì nồng độ thuốc trong máu của bệnh nhân cao nhất?
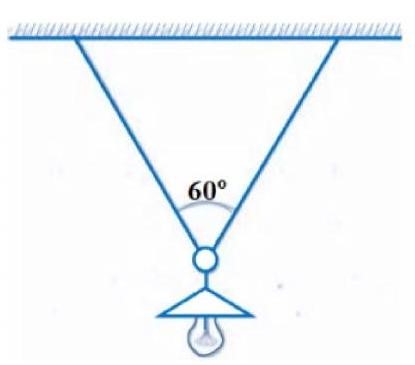
Người ta treo một bóng đèn có khối lượng \(m = 1{\rm{\;kg}}\) bằng cách luồn sợi dây qua một cái móc của đèn và hai đầu dây được gắn chặt trên trần nhà. Hai nửa sợi dây có chiều dài bằng nhau và hợp với nhau một góc bằng \({60^ \circ }\). Tính lực căng của mỗi nửa sợi dây là bao nhiêu? Lấy \(g = 10{\rm{\;m}}/{{\rm{s}}^2}\). (làm tròn kết quả đến hàng phần trăm)
