Bộ 20 đề thi Giữa kì 1 Toán 12 Kết nối tri thức có đáp án - Đề 17
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hàm số \(y = {x^4} - 8{x^2} - 4\). Hàm số đã cho nghịch biến trên các khoảng.
\(\left( { - 2\,;\,0} \right)\) và \(\left( {0\,;\,2} \right)\).
\(\left( { - \infty \,;\, - 2} \right)\) và \(\left( {0\,;\,2} \right)\).
\(\left( { - \infty \,;\, - 2} \right)\)và \(\left( {2\,;\, + \infty } \right)\).
\(\left( { - 2\,;\,0} \right)\) và \(\left( {2\,;\, + \infty } \right)\).
Cho hàm số \[y = f\left( x \right)\] liên tục trên đoạn \[\left[ { - 1;\;2} \right]\] và có đồ thị như hình vẽ bên. Gọi \[M\], \[m\] lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn \[\left[ { - 1;\;2} \right]\]. Ta có \[2M + m\] bằng 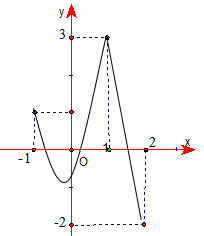
\[4\].
\[5\].
\[3\].
\[0\].
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu \(\left( S \right):{\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 1} \right)^2} = 9.\) Tìm tọa độ tâm \(I\) và bán kính \(R\) của mặt cầu \(\left( S \right).\)
\(I\left( {1; - 2; - 1} \right)\)và \(R = 9.\)
\(I\left( { - 1;2;1} \right)\) và\(R = 9.\)
\(I\left( { - 1;2;1} \right)\) và \(R = 3.\)
\(I\left( {1; - 2; - 1} \right)\) và \(R = 3.\)
Cho hàm số \(y = f(x)\) xác định trên \(\mathbb{R}\backslash \left\{ 1 \right\}\), liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình dưới đây. Hỏi đồ thị hàm số đã cho có bao nhiêu đường tiệm cận? 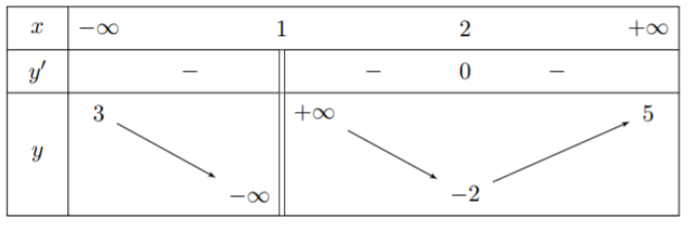
\(4\).
\(1\).
\(2\).
\(3\).
Trong không gian với hệ tọa độ Oxyz, cho hai điểm \[A\left( {1;2;3} \right)\] và \[B\left( {5;2;0} \right)\]. Khi đó:
\(\left| {\overrightarrow {AB} } \right| = \sqrt {61} \).
\(\left| {\overrightarrow {AB} } \right| = 3\).
\(\left| {\overrightarrow {AB} } \right| = 5\).
\(\left| {\overrightarrow {AB} } \right| = 2\sqrt 3 \).
Trong không gian với hệ tọa độ Oxyz cho điểm \(A\left( {1; - 4; - 5} \right)\). Tọa độ điểm \(A'\)đối xứng với điểm \(A\)qua mặt phẳng \(Oxz\)là
\(\left( {1; - 4;5} \right)\).
\(\left( {1;4; - 5} \right)\).
\(\left( { - 1;4;5} \right)\).
\(\left( {1;4;5} \right)\).
Trong không gian với hệ trục tọa độ Oxyz, cho tam giác \(ABC\) có tọa độ các đỉnh là \(A\left( {2;1; - 1} \right),\)\(B\left( {3;2; - 2} \right),C\left( {1;0;0} \right).\) Khoảng cách từ gốc \(O\) đến trọng tâm của tam giác \(ABC\) bằng
\(3\sqrt 2 \).
\(\sqrt 6 \).
\(2\).
\(2\sqrt 3 \).
Cho tứ diện \(ABCD\)có \(G\)là trọng tâm tam giá\(BCD\) Khẳng định nào sau đây đúng?
\(\overrightarrow {AG} = \frac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} } \right)\).
\(\overrightarrow {AG} = \frac{2}{3}\left( {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} } \right)\).
\(\overrightarrow {AG} = - \frac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} } \right)\).
\(\overrightarrow {AG} = - \frac{2}{3}\left( {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} } \right)\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đạo hàm \(f'\left( x \right) = {\left( {x + 1} \right)^{2019}}{\left( {x - 1} \right)^{2020}}\left( {2 - x} \right)\). Hàm số \(y = f\left( x \right)\) có bao nhiêu điểm cực trị?
\(6\).
\(2\).
\(3\).
\(3\).
Cho hàm số \(y = \frac{{ax + 2}}{{bx + c}}\) có đồ thị như hình sau
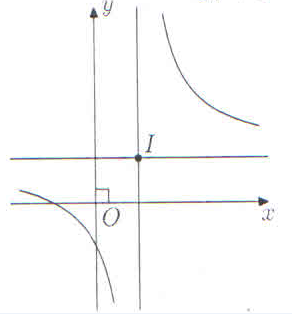
Trong các số \(a,\,\;b\) và \(c\) có bao nhiêu số dương?
0.
1.
3.
2.
Bảng biến thiên trong hình dưới bên dưới của hàm số nào dưới đây?
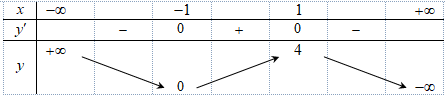
\(y = {x^3} - 3x + 4\).
\(y = \frac{{x - 1}}{{2x - 1}}\).
\(y = {x^4} - 2{x^2} - 3\).
\(y = - {x^3} + 3x + 2\).
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số \[y = \frac{{x + m}}{{x + 1}}\] trên đoạn \(\left[ {1;2} \right]\) bằng 8 (m là tham số thực). Khẳng định nào sau đây đúng?
\(8 < m < 10\).
\(m > 10\).
\(0 < m < 4\).
\(4 < m < 8\).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(y = x{}^3 - 3x + 2\). Xét tính đúng – sai của các mệnh đề sau:
a) Hàm số đồng biến trên \(\mathbb{R}\).
b) Hàm số có một cực trị là \(0\).
c) Với \(m \in \left( {0;4} \right)\) thì phương trình \({x^3} - 3x + 2 - m = 0\) có ba nghiệm phân biệt.
d) Đồ thị hàm số đi qua điểm \(L\left( {2;5} \right)\).
Trong không gian với hệ tọa độ Oxyz, cho hình bình hành \(ABCD\) có \(A\left( { - 3;4;2} \right)\), \(B\left( { - 5;6;2} \right)\), \(C\left( { - 10;17; - 7} \right)\).
a) \(\overrightarrow {AB} .\overrightarrow {AD} = 10\).
b) Tọa độ trực tâm của tam giác \(ABD\) là \(H\left( { - 5;12;4} \right)\).
c) Tọa độ trọng tâm của tam giác \(ABC\) là \(G\left( { - 6;9; - 1} \right)\).
d) Tọa độ trung điểm của \(AB\) là \(I\left( { - 4;5;2} \right)\).
Cho hàm số \(y = f(x) = \frac{{{x^2} - x + 2}}{{x - 2}}\)có đồ thị \(\left( C \right)\).
a) Đồ thị \(\left( C \right)\)có tiệm cận đứng là đường thẳng \(x = 2\),
b) Đường thẳng\(y = x + 1\)là tiệm cận xiên của đồ thị \(\left( C \right)\).
c) Đồ thị \(\left( C \right)\)đi qua điểm \(M\left( {0;2} \right)\).
d) Đường thẳng \(y = m\) cắt đồ thị \(\left( C \right)\)tại hai điểm phân biệt khi \( - 1 < m < 7\).
Một sợi dây kim loại dài \(60cm\) được cắt thành hai đoạn. Đoạn dây thứ nhất uốn thành hình vuông cạnh \(a\), đoạn dây thứ hai uốn thành đường tròn bán kính \(r\).
a) \(\,r = \frac{{60 - 2a}}{\pi }.\)
b) Nếu cắt sợi dây thành hai đoạn bằng nhau và vẫn uốn thành một hình vuông và một hình tròn thì hình tròn có diện tích lớn hơn hình vuông.
c) Tổng diện tích của hình vuông và hình tròn là \(\frac{1}{\pi }\left[ {\left( {\pi + 4} \right){a^2} - 120a + 900} \right]\).
d) Để tổng diện tích của hình vuông và hình tròn nhỏ nhất thì tỉ số \(\frac{a}{r}\) bằng \(\frac{1}{2}.\)
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Một nhà máy sản xuất \(x\) sản phẩm trong mỗi tháng. Chi phí sản xuất \(x\) sản phẩm được cho bởi hàm chi phí \(C\left( x \right) = 16000 + 500x - 1,6{x^2} + 0,004{x^3}\) (nghìn đồng). Biết giá bán của mỗi sản phẩm là một hàm số phụ thuộc vào số lượng sản phẩm \(x\) và được cho bởi công thức \(p\left( x \right) = 1700 - 7x\) (nghìn đồng). Hỏi mỗi tháng nhà máy nên sản xuất bao nhiêu sản phẩm để lợi nhuận thu được là lớn nhất? Biết rằng kết quả khảo sát thị trường cho thấy sản phẩm sản xuất ra sẽ tiêu thụ hết.
Một người có một dây ruy băng dài 130 cm, người đó cần bọc dải ruy băng này quanh một hộp quà hình trụ. Khi bọc quà, người này dùng 10 cm của dải ruy băng để thắt nơ ở trên nắp hộp (như hình vẽ). Dải ruy băng có thể bọc được hộp quà có thể tích bằng \(a.\pi \left( {c{m^3}} \right),a \in {\mathbb{N}^*}\). Giá trị lớn nhất của \(a\) là bao nhiêu?

Một cửa hàng trung bình bán được 100 cái Tivi mỗi tháng với giá 14 triệu đồng một cái. Chủ cửa hàng nhận thấy rằng, nếu giảm giá bán mỗi cái 500 ngàn đồng thì số lượng tivi bán ra sẽ tăng thêm 10 cái mỗi tháng. Hỏi cửa hàng nên bán với giá bao nhiêu để doanh thu cửa hàng là lớn nhất?
Hai chiếc kinh khí cầu A và B bay lên từ cùng một vị trí O trên mặt đất. Sau một khoảng thời gian, kinh khí cầu A nằm cách điểm xuất phát \(4\,km\) về phía Đông và \(3\,km\) về phía Nam, đồng thời cách mặt đất \(1\,km\); kinh khí cầu B nằm cách điểm xuất phát \(1\,km\) về phía Bắc và \(1\,,5\,km\) về phía Tây, đồng thời cách mặt đất \(0,8\,km\)(hình minh họa bên dưới). Cùng thời điểm đó, một người đứng trên mặt đất và nhìn thấy hai kinh khí cầu nói trên. Biết rằng, so với các vị trí quan sát khác trên mặt đất, vị trí người đó đứng có tổng khoảng cách đến hai kinh khí cầu là nhỏ nhất. Hỏi tổng khoảng cách nhỏ nhất ấy bằng bao nhiêu kilômét? (Làm tròn kết quả đến hàng phần trăm).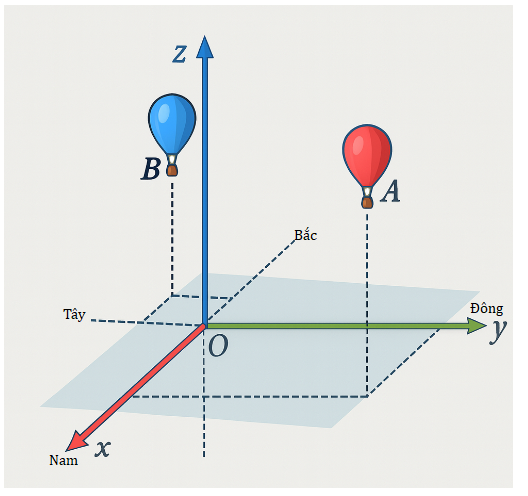
Có ba lực cùng tác động vào một vật. Hai trong ba lực này hợp với nhau một góc 1200 và có độ lớn lần lượt là 10 N và 8 N. Lực thứ ba vuông góc với mặt phẳng tạo bởi hai lực đã cho và có độ lớn 6 N. Tính độ lớn của hợp lực của ba lực trên. (Làm tròn kết quả đến hàng đơn vị)
Giám đốc một nhà hát A đang phân vân trong việc xác định mức giá vé xem các chương trình được trình chiếu trong nhà hát. Việc này rất quan trọng nó sẽ quyết định nhà hát thu được bao nhiêu lợi nhuận từ các buổi trình chiếu. Theo những cuốn sổ ghi chép của mình, ông ta xác định được rằng: nếu giá vé vào cửa là \(20\) USD/người thì trung bình có \(1000\) người đến xem. Nhưng nếu tăng thêm \(1\) USD/người thì sẽ mất \(100\) khách hàng hoặc giảm đi \(1\) USD/người thì sẽ có thêm \(100\) khách hàng trong số trung bình. Biết rằng, trung bình, mỗi khách hàng còn đem lại \(2\) USD lợi nhuận cho nhà hát trong các dịch vụ đi kèm. Hãy giúp giám đốc nhà hát này xác định xem cần tính giá vé vào cửa là bao nhiêu để thu nhập là lớn nhất.








