Bộ 20 đề thi Giữa kì 1 Toán 12 Kết nối tri thức có đáp án - Đề 19
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho 2 vec tơ \(\overrightarrow u = \left( {x;y;z} \right),\overrightarrow v = \left( {x';y';z'} \right).\) Tìm công thức đúng.
\(\cos \left( {\overrightarrow u ,\overrightarrow v } \right) = \frac{{\left| {x.x' + y.y' + z.z'} \right|}}{{\sqrt {\left( {{x^2} + {y^2} + {z^2}} \right)} + \sqrt {\left( {x{'^2} + y{'^2} + z{'^2}} \right)} }}.\)
\(\cos \left( {\overrightarrow u ,\overrightarrow v } \right) = \frac{{\left| {x.x' + y.y' + z.z'} \right|}}{{\sqrt {\left( {{x^2} + {y^2} + {z^2}} \right).\left( {x{'^2} + y{'^2} + z{'^2}} \right)} }}.\)
\(\cos \left( {\overrightarrow u ,\overrightarrow v } \right) = \frac{{x.x' + y.y' + z.z'}}{{\sqrt {\left( {{x^2} + {y^2} + {z^2}} \right)} + \sqrt {\left( {x{'^2} + y{'^2} + z{'^2}} \right)} }}.\)
\(\cos \left( {\overrightarrow u ,\overrightarrow v } \right) = \frac{{x.x' + y.y' + z.z'}}{{\sqrt {\left( {{x^2} + {y^2} + {z^2}} \right).\left( {x{'^2} + y{'^2} + z{'^2}} \right)} }}.\)
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên bên dưới. Gọi \[M,{\rm{ }}m\] lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) khi \(x \in \left[ { - 3;3} \right]\). Giá trị \(M - 2m\) bằng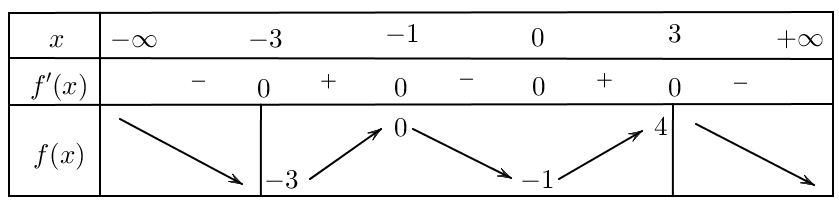 
\(10\).
\(f\left( 2 \right)\).
\(6\).
\( - 2\).
Hàm số \(y = \sqrt {2x - {x^2}} \) nghịch biến trên khoảng nào dưới đây?
\(\left( { - \infty ;1} \right)\).
\(\left( {0;1} \right)\).
\(\left( {1; + \infty } \right)\).
\(\left( {1;2} \right)\).
Hàm số \(y = f\left( x \right)\)liên tục trên \(\mathbb{R}\backslash \left\{ { - 2} \right\}\) và có bảng biến thiên như sau: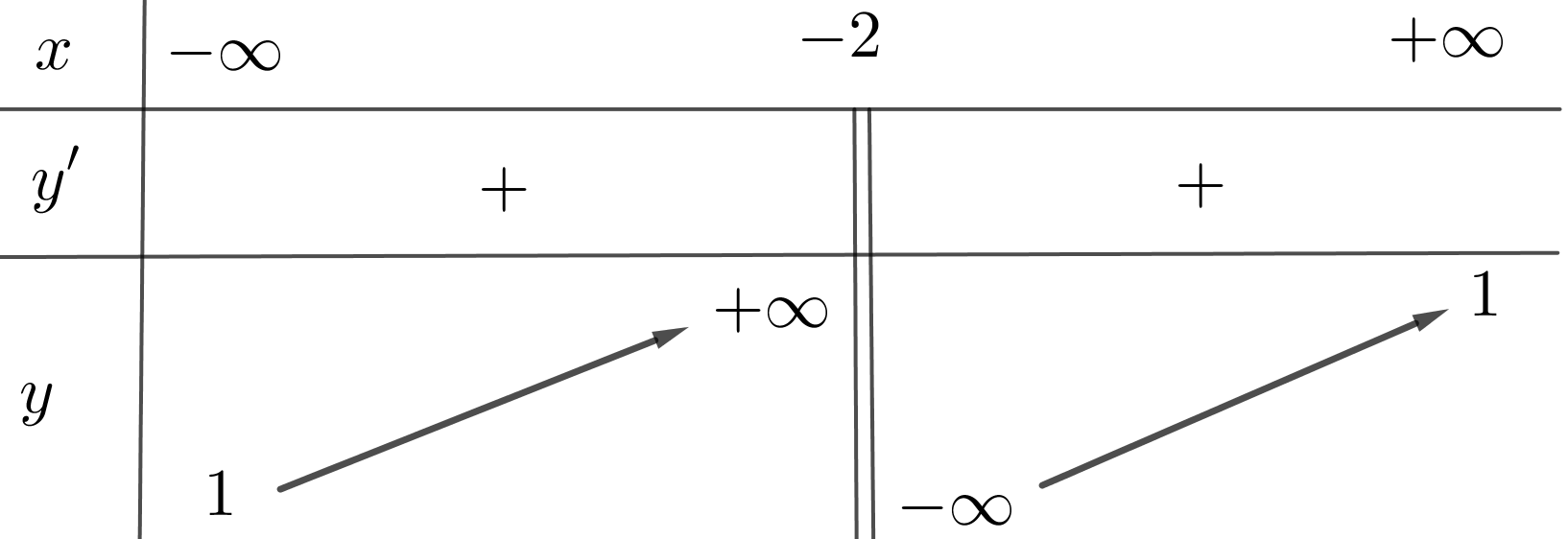
Số các đường tiệm cận của đồ thị hàm số \(y = f\left( x \right)\)là
\(2\).
\(4\).
\(3\).
\(1\).
Trong không gian Oxyz, cho hai điểm \(A\left( { - 1;2;3} \right)\), \(B\left( {1;0;2} \right)\). Độ dài đoạn thẳng \(AB\) bằng
\(3\).
\(\sqrt 5 \).
\(9\).
\(\sqrt {29} \).
Trong không gian Oxyz mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} - 8x + 4y + 2z - 4 = 0\) có bán kính \(R\) là
\[R = 2\].
\[R = \sqrt 5 \].
\[R = 25\].
\[R = 5\].
Trong không gian Oxyz, cho ba điểm \(A\left( { - 1;\,0;\,2} \right)\), \(B\left( {2;\,1;\, - 3} \right)\) và \(C\left( {1;\, - 1;\,0} \right)\). Tìm tọa độ điểm \(D\) sao cho \(ABCD\) là hình bình hành.
\[D\left( { - 2;\,2;\,5} \right)\].
\[D\left( {0;\,2;\, - 1} \right)\].
\[D\left( { - 2;\, - 2;\,5} \right)\].
\[D\left( {2;\,2;\, - 5} \right)\].
Cho hình lăng trụ ABC.A'B'C', M là trung điểm của \(BB'\). Đặt \(\overrightarrow {CA} = \overrightarrow a \), \(\overrightarrow {CB} = \overrightarrow b \), \[\overrightarrow {AA'} = \overrightarrow c \] (Tham khảo hình vẽ).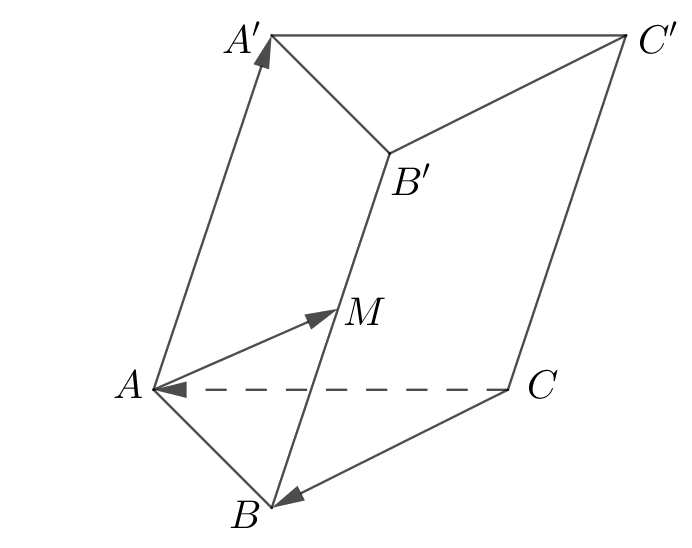
Khẳng định nào sau đây đúng?
\(\overrightarrow {AM} = \overrightarrow b - \overrightarrow a + \frac{1}{2}\overrightarrow c \).
\(\overrightarrow {AM} = \overrightarrow a - \overrightarrow c + \frac{1}{2}\overrightarrow b \).
\(\overrightarrow {AM} = \overrightarrow a + \overrightarrow c - \frac{1}{2}\overrightarrow b \).
\(\overrightarrow {AM} = \overrightarrow b + \overrightarrow c - \frac{1}{2}\overrightarrow a \).
Cho hàm số \(y = - {x^2} + 4x - m\) (\(m\) là tham số thực) thỏa mãn \[\mathop {\min }\limits_{\left[ { - 1;3} \right]} y + \mathop {\max }\limits_{\left[ { - 1;3} \right]} y = 1\]. Khẳng định nào sau đây đúng?
\( - 7 < m < 0\).
\(m < - 10\).
\( - 10 < m \le - 7\).
\(0 < m < 10\).
Cho hàm số \(y = f\left( x \right)\)liên tục trên \(\mathbb{R}\)và có đồ thị như hình vẽ. Mệnh đề nào sau đây sai?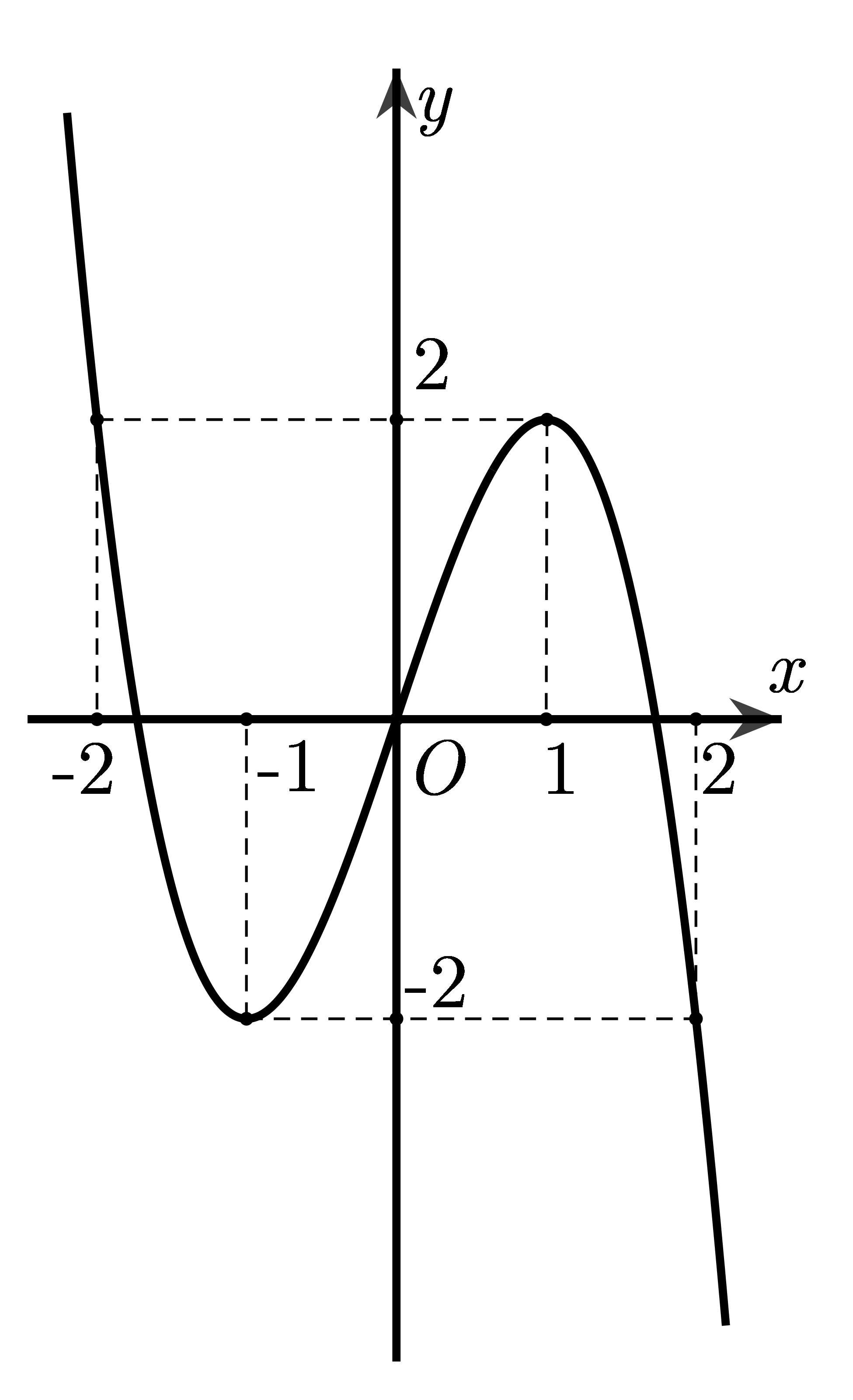 
Hàm số \(y = f\left( x \right)\)có cực tiểu bằng \( - 1\).
Nếu \(\left| m \right| > 2\)thì phương trình \(f\left( x \right) = m\)có nghiệm duy nhất.
Giá trị lớn nhất của hàm số \(y = f\left( x \right)\)trên đoạn \(\left[ { - 2;\,2} \right]\)bằng \(2\).
Hàm số \(y = f\left( x \right)\)có hai điểm cực trị.
Hàm số nào sau đây có bảng biến thiên như hình vẽ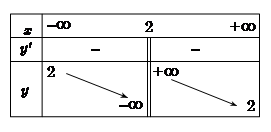
\(y = \frac{{2x - 1}}{{x - 2}}\).
\(y = \frac{{2x - 3}}{{x + 2}}\).
\(y = \frac{{x + 3}}{{x - 2}}\).
\(y = \frac{{2x - 5}}{{x - 2}}\).
Cho hàm số \[y = f(x)\]có đạo hàm \[f'(x) = x(x - 1){(x + 2)^3}{(x - 2)^2}\], \[\forall x \in \mathbb{R}\]. Số điểm cực trị của hàm số đã cho là
\[2\].
\[7\].
\[3\].
\[4\].
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Một khúc gỗ có dạng hình khối nón có bán kính đáy \(r = 2m\), chiều cao \(l = 6m\). Bác thợ mộc chế tác từ khúc gỗ đó thành một khúc gỗ có dạng hình khối trụ như hình vẽ.
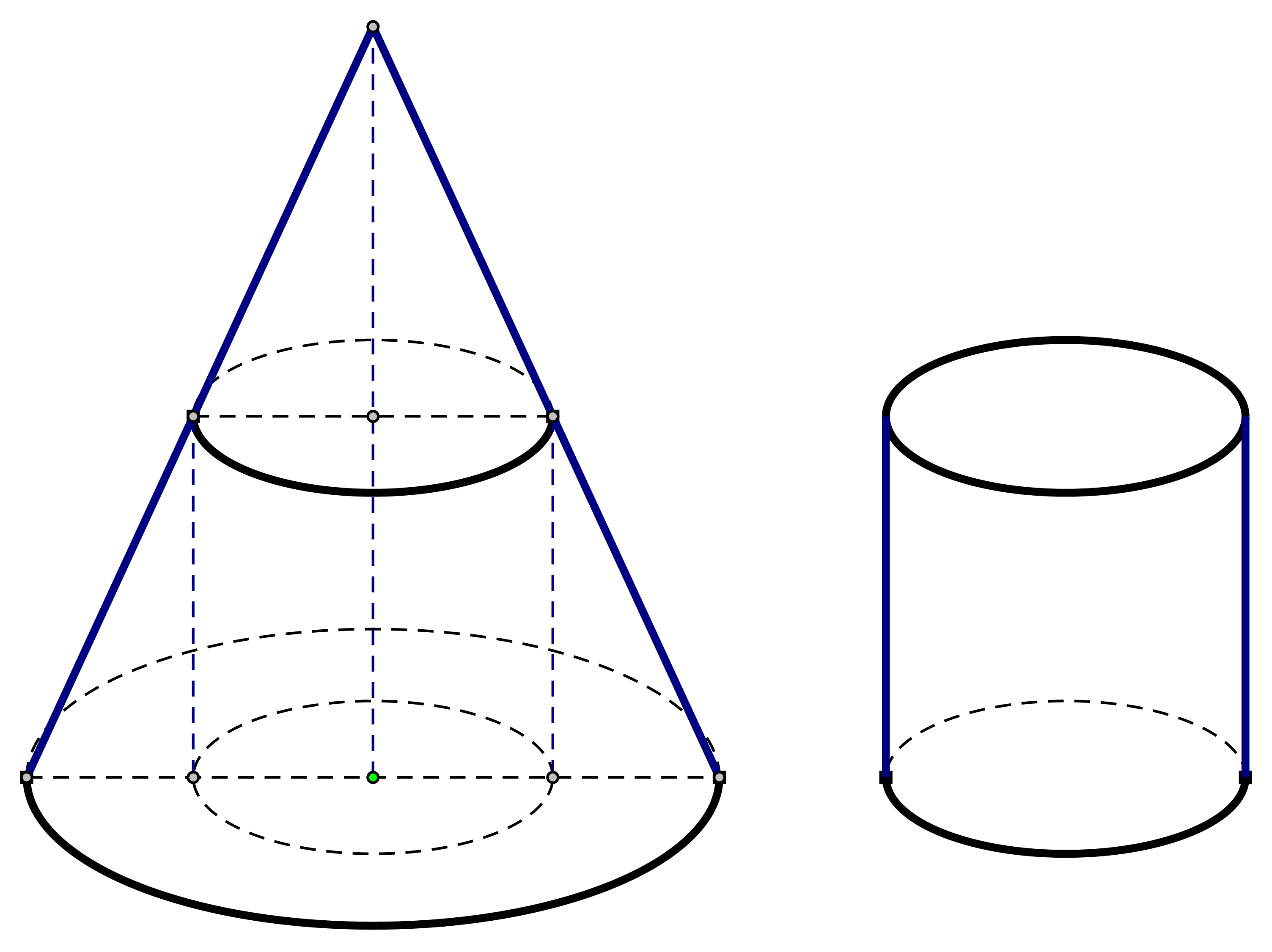
Xét tính đúng sai của các mệnh đề sau:
a) Giả sử bác thợ mộc chế tác khúc gỗ đó thành hình trụ có bán kính đáy bằng chiều cao, khi đó thể tích của khối trụ là \[V = \frac{{27}}{8}\pi \left( {{m^3}} \right) \cdot \]
b) Ta có mặt cắt qua trục hình nón như hình vẽ. Đặt \(x\) là bán kính đáy hình trụ, \(h\) là chiều cao của hình trụ.
c) Hàm số xác định thể tích của khối trụ trên là \[V = 6{x^2} - 3{x^3}\left( {{m^3}} \right),{\rm{ }}\forall x \in \left( {0;2} \right)\].
d) Thể tích lớn nhất của khối gỗ mà bác thợ mộc chế tác là \({V_{\max }} = \frac{{32\pi }}{9}\left( {{m^3}} \right)\).
Cho hàm số \(y = \frac{{m{x^2} + \left( {3{m^2} - 2} \right)x - 2}}{{x + 3m}}\)\(\left( 1 \right)\) với \(m\) là số thực.
a) Khi \(m = 1\) giao điểm của đường tiệm cận xiên và tiệm cận đứng của đồ thị hàm số là \(I\left( {3; - 5} \right)\).
b) Khi \(m = 1\) đồ thị hàm số có đường tiệm cận xiên là \(y = x - 2\).
c) Khi \(m = 1\) đồ thị hàm số có 2 điểm cực trị.
d) Có 2 giá trị \(m\) để góc giữa hai tiệm cận của đồ thị hàm số \(\left( 1 \right)\) bằng \({45^0}\).
Cho hàm số \(y = f(x) = {e^{ - {x^2}}}\). Nêu tính đúng sai của các khẳng định sau:
a) Hàm số đạt cực đại tại điểm \(x = 0.\)
b) \(\mathop {\min }\limits_\mathbb{R} f(x) = f(0) = 1.\)
c) \(y = 0\)là đường tiệm cận ngang của đồ thị hàm số.
d) Hàm số đồng biến trên khoảng \(( - \infty ;0)\).
Cho hai véctơ \(\vec u = \left( {0;2;3} \right)\) và \(\vec v = \left( {m - 1;2m;3} \right)\).
a) \(\left| {\vec u\left| = \right|\vec v} \right| \Leftrightarrow m = - \frac{3}{5}\).
b) \(\left| {\vec u} \right| = \sqrt {13} \).
c) \(\vec u = \vec v \Leftrightarrow m = 1\).
d) \(\vec u \bot \vec v \Leftrightarrow m = \frac{9}{4}\).
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Một thiết bị thăm dò đáy biển như hình vẽ được đẩy bởi một lực \(\vec f = \left( {5;4; - 2} \right)\) (đơn vị: N) giúp thiết bị thực hiện độ dời \(\vec a = \left( {70;20; - 40} \right)\) (đơn vị: m). Tính công sinh bởi lực \(\vec f\).
Vận tốc của một tàu con thoi từ lúc cất cánh tại thời điểm \[t = 0\,\,\left( s \right)\] cho đến thời điểm \[t = 126\,\,\left( s \right)\] được cho bởi công thức \[v(t) = 0,001302{t^3} - 0,09029{t^2} + 83\] (vận tốc được tính bằng đơn vị \[ft/s\]). Hỏi tại thời điểm tàu con thoi đạt gia tốc nhỏ nhất thì vận tốc tàu con thoi gần bằng bao nhiêu? (Kết quả làm tròn đến hàng phần mười).
Giả sử một công ty du lịch bán tour với giá là \(x\) (triệu đồng)/khách thì doanh thu sẽ được biểu diễn qua hàm số \(f(x) = - 200{x^2} + 550x\). Công ty phải bán giá tour cho một khách là bao nhiêu để doanh thu từ tua xuyên Việt là lớn nhất (làm tròn tới hàng phần trăm).
Khi máu di chuyển từ tim qua các động mạch chính rồi đến các mao mạch và quay trở lại qua các tĩnh mạch, huyết áp tâm thu ( tức là áp lực của máu lên động mạch khi tim co bóp) liên tục giảm xuống. Giả sử một người có huyết áp tâm thu P ( được tính bằng mmHg) được cho bởi hàm số: \(\) \(P(t) = \frac{{25{t^2} + 125}}{{{t^2} + 1}},0 \le t \le 10\)Trong đó t là thời gian được tính bằng giây. Tốc độ thay đổi của huyết áp sau 8 giây kể từ khi máu rời tim giảm bao nhiêu mmHg?
Có ba lực \({F_1},{F_2},{F_3}\) cùng tác động vào một vật. Ba lực này đôi một hợp với nhau một góc 600 và có độ lớn lần lượt là \(3\;N,6\;N\) và \[9N\]. Tính độ lớn \((N)\) của hợp lực của ba lực trên.
Cho hàm số \(y = \frac{{mx + 2015m + 2016}}{{ - x - m}}\) với \(m\) là tham số thực. Gọi \(S\) là tập hợp các giá trị nguyên của \(m\) để hàm số đồng biến trên từng khoảng xác định. Tính số phần tử của \(S\).
