Bộ 20 đề thi Giữa kì 1 Toán 12 Kết nối tri thức có đáp án - Đề 14
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 3;3} \right]\) và có bảng biến thiên bên dưới. Tìm giá trị lớn nhất \(M\)và giá trị nhỏ nhất \(m\)của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ { - 3;3} \right]\).
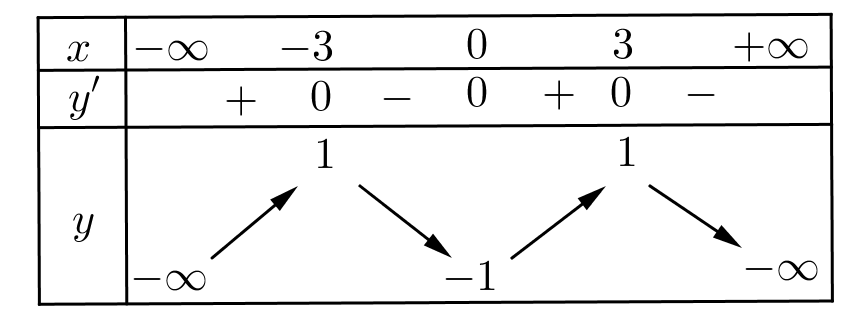
\(M = 1;\;m = - 1\).
\(M = 3;\;m = - 4\).
\(M = - 1;\;m = 1\)
\(M = 3;\;m = - 3\).
Trong không gian với hệ tọa độ Oxyz cho hai điểm \(A\left( {0;0; - 6} \right)\), \(B\left( {8;0;0} \right)\). Độ dài đoạn thẳng \(AB\) bằng
\(14\).
\(100\).
\(2\).
\(10\).
Trong không gian Oxyz, cho hai vectơ \[\overrightarrow a \left( {2\,;\,3\,;\,1} \right)\], \[\overrightarrow b \left( { - 2\,;\,1\,;\,2} \right)\]. Khi đó \[\left[ {\overrightarrow a \,,\,\overrightarrow b } \right]\] có tọa độ
\[\left( {2\,;\,1\,;\,0} \right)\].
\[\left( {2\,;\,0\,;\,1} \right)\].
\[\left( {0\,;\,4\,;\,3} \right)\].
\[\left( {5\,;\, - 6\,;\,8} \right)\].
Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên sau![Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên sau Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là A. \(3.\) B. \(1.\) C. \(4.\) D. \(2.\) (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/16-1761646679.png)
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là
\(3.\)
\(1.\)
\(4.\)
\(2.\)
Cho hàm số \(y = f(x)\) xác định và liên tục trên \(\mathbb{R}\) có đồ thị như hình vẽ bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?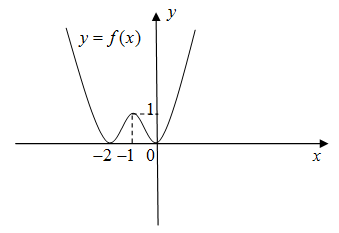
\(\left( { - 2\,;\,0\,} \right)\).
\(\left( {0\,;\,1\,} \right)\).
\(\left( { - 2\,;\, - 1\,} \right)\).
\(\left( { - 1\,;\,0\,} \right)\).
Trong không gian Oxyz, cho ba vectơ \[\vec a = \left( {1\;;\; - 1\;;\;2} \right)\], \[\vec b = \left( {3\;;\;0\;;\; - 1} \right)\] và \[\vec c = \left( { - 2\;;\;5\;;\;1} \right)\]. Vectơ \[\overrightarrow d = \overrightarrow a + \overrightarrow b - \overrightarrow c \] có tọa độ là
\[\left( {6\;;\;0\;;\; - 6} \right).\]
\[\left( { - 6\;;\;6\;;\;0} \right).\]
\[\left( {0\;;\;6\;;\; - 6} \right).\]
\[\left( {6\;;\; - 6\;;\;0} \right).\]
Tìm \(a\) để giá trị lớn nhất của hàm số \(y = {x^3} - 3a{x^2} + a - 1\) trên đoạn \(\left[ { - 1;a} \right]\) bằng 10, biết \(a > 0\).
\(a = 11\).
\(a = \frac{5}{2}\).
\(a = \frac{3}{2}\).
\(a = 10\).
Trong không gian với hệ trục toạ độ Oxyz, cho hình bình hành \(ABCD\) với \(A\left( { - 2;3;1} \right)\);\(B\left( {3;0; - 1} \right)\),\(C\left( {6;5;0} \right)\). Toạ độ đỉnh \(D\) là
\(D\left( {1;8;2} \right)\).
\(D\left( {11;2;2} \right)\).
\(D\left( {11;2; - 2} \right)\).
\(D\left( {1;8; - 2} \right)\).
Bảng biến thiên sau đây là của hàm số nào?
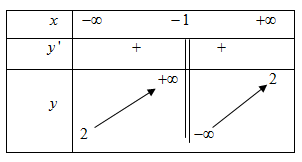
\[y = \frac{{x + 1}}{{2x - 1}}\].
\[y = \frac{{2x - 1}}{{x - 1}}\].
\[y = \frac{{2x - 1}}{{x + 1}}\].
\[y = \frac{{2x + 3}}{{x + 1}}\].
Cho hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right) = x{\left( {x + 2} \right)^2}\), \(\forall x \in \mathbb{R}\). Số điểm cực trị của hàm số đã cho là
\(0\).
\(2\).
\(3\).
\(1\).
Cho hình hộp ABCD.A'B'C'D'. Chọn đẳng thức đúng: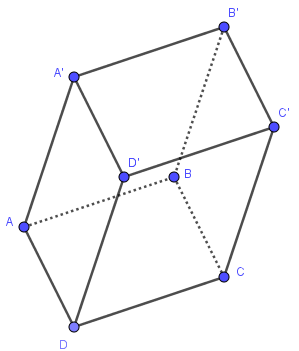 
\[\overrightarrow {AB'} = \overrightarrow {AB} + \overrightarrow {AA'} + \overrightarrow {AD} \].
\[\overrightarrow {DB} = \overrightarrow {DA} + \overrightarrow {DD'} + \overrightarrow {DC} \].
\[\overrightarrow {BD'} = \overrightarrow {BA} + \overrightarrow {BC} + \overrightarrow {BB'} \].
\[\overrightarrow {AC'} = \overrightarrow {AC} + \overrightarrow {AB} + \overrightarrow {AD} \].
Giả sử hàm số \[y = a{x^4} + b{x^2} + c\] có đồ thị là hình bên dưới.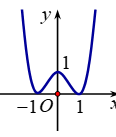
Khẳng định nào sau đây là khẳng định đúng?
\(a < 0,\;b > 0,\;c = 1\).
\(a > 0,\;b > 0,\;c > 0\).
\[a > 0,\,\,b < 0,\,\,c = 1\].
\[a > 0,\,\,b > 0,\,\,c = 1\].
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \(y = f\left( x \right)\) có điểm cực tiểu \({x_1}\) và điểm cực đại \({x_2}\). Khi đó
a) \(f\left( {{x_1}} \right),f\left( {{x_2}} \right)\)là các cực trị của hàm số \(y = f\left( x \right)\);
b) \({x_1} < {x_2}\);
c) \(f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).
d) \({x_1}\)và \({x_2}\) là các điểm cực trị của hàm số \(y = f\left( x \right)\);
Cho hàm số \(y = f\left( x \right)\) là hàm bậc hai trên bậc nhất, có đồ thị ở hình bên dưới.
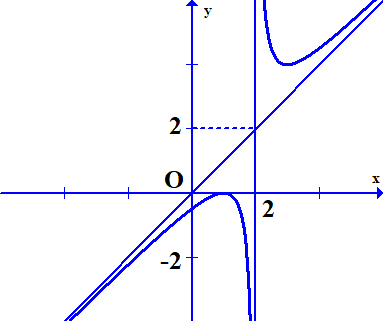
a) Tập xác định của hàm số là \(D = \mathbb{R}\backslash \left\{ 2 \right\}\).
b) Hàm số đồng biến trên khoảng \(\left( { - \infty \,;0} \right)\).
c) Đồ thị \[\left( C \right)\] có đường tiệm xiên \(y = x + 2\).
d) Tâm đối xứng của đồ thị hàm số có toạ độ là:\(\left( {2;2} \right)\).
Một cơ sở sản xuất khăn mặt đang bán mỗi chiếc khăn với giá \(30\,000\) đồng một chiếc và mỗi tháng cơ sở bán được trung bình \(3000\) chiếc khăn. Cơ sở sản xuất đang có kế hoạch tăng giá bán để có lợi nhận tốt hơn. Sau khi tham khảo thị trường, người quản lý thấy rằng nếu từ mức giá \(30\,000\) đồng mà cứ tăng giá thêm \(1000\) đồng thì mỗi tháng sẽ bán ít hơn \(100\) chiếc. Biết vốn sản xuất một chiếc khăn không thay đổi là \(18\,000\).
a) Để đạt lợi nhuận lớn nhất thì sau khi tăng giá mỗi chiếc khăn lãi \[21000\] đồng.
b) Để đạt lợi nhuận lớn nhất thì mỗi chiếc khăn cần bán với giá \[39000\] đồng.
c) Để đạt lợi nhuận lớn nhất thì mỗi chiếc khăn cần tăng thêm \[10000\] đồng.
d) Để đạt lợi nhuận lớn nhất thì số khăn bán ra giảm \[800\] chiếc.
Trong không gian với hệ trục toạ độ Oxyz, cho vectơ \(\overrightarrow a = 2\overrightarrow i + \overrightarrow j - 3\overrightarrow k \).
a) Toạ độ của vectơ\[2\overrightarrow a - \overrightarrow j \] là \[\left( {4;2; - 6} \right)\].
b) Toạ độ của vectơ \[\overrightarrow a \] là \[\left( {2;1; - 3} \right)\].
c) Độ dài của vectơ \[\overrightarrow a \] là \[14\].
d) Trong không gian \(Oxyz,\) biết \(\overrightarrow u = x\overrightarrow i + y\overrightarrow j + z\overrightarrow k \). Khi đó toạ độ của vectơ \[\overrightarrow u \] là \[\left( {x;y;z} \right)\].
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Lát cắt ngang của một vùng đất ven biển được mô hình hoá thành một hàm số bậc ba \[y = f\left( x \right)\] có đồ thị như hình vẽ (đơn vị độ dài trên các trục là km).
![Lát cắt ngang của một vùng đất ven biển được mô hình hoá thành một hàm số bậc ba \[y = f\left( x \right)\] có đồ thị như hình vẽ (đơn vị độ dài trên các trục là km). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/3-1761647380.jpg)
Biết khoảng cách hai bên chân đồi \(OA = 2\,\,{\rm{km}}\), độ rộng của hồ \(AB = 1\,\,{\rm{km}}\) và ngọn đồi cao \[528\,\,{\rm{m}}\]. Tìm độ sâu của hồ (tính bằng mét) tại điểm sâu nhất? (làm tròn đến hàng đơn vị).
Một bể chứa 3000 lít nước tinh khiết. Người ta bơm vào bể đó nước muối có nồng độ 40 gam muối cho mỗi lít nước vởi tốc độ 30 lít/phút. Gọi \(f\left( t \right)\) là nồng độ muối trong bể sau \(t\) phút. khi \(t\) càng lớn thì nồng độ muối trong bể sẽ tiến gần đến mức \(x\) (gam/lít). Tính \(x\) (làm tròn đến hàng đơn vị)
Doanh số bán hàng của một loại sản phẩm (chục triệu đồng) trong một phiên livestream bán hàng kéo dài sáu giờ theo quy luật hàm số \(f(t) = \frac{{3t}}{{{e^{\frac{t}{2}}}}},0 \le t \le 6\) trong đó thời gian \(t\) được tính bằng giờ kể từ khi bắt đầu livestream.
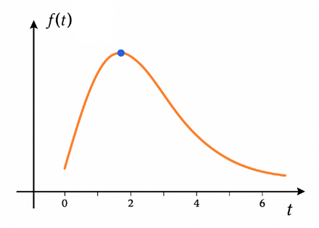
Khi đó, đạo hàm \(f\prime (t)\) sẽ biểu thị tốc độ bán hàng. Hỏi sau bao nhiêu giờ kể từ khi bắt đầu phiên livestream thì doanh số bán hàng là lớn nhất?
Một chiếc xe đang kéo căng sợi dây cáp \(AB\) trong công trường xây dựng, trên đó đã thiết lập hệ toạ độ \(Oxyz\) như hình vẽ dưới với độ dài đơn vị trên các trục tọa độ bằng \(1m\). Biết \(\overrightarrow {AB} = \left( {x;y;z} \right)\). Tính \(x + 2y - z\)(làm tròn đến hàng phần mười).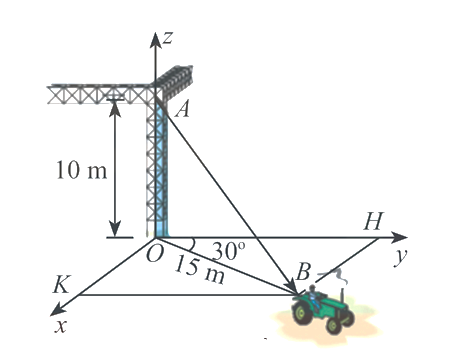
Người ta vận chuyền một thùng hàng có dạng hình hộp chữ nhật bằng tách móc 4 dây cáp vào 4 góc trên của thùng hàng và đầu còn lại móc vào cần cầu như hình vẽ. Biết rằng các đoạn dây cáp có độ dài bằng nhau và góc tạo bởi hai đoạn dây cáp đối diện nhau là 60°. Chiếc cần cẩu kéo thùng hàng lên theo phương thẳng đứng. Biết rằng F1, F2,F3, F4 biểu diễn lực căng của 4 sợi dây, chịu được tối đa lực căng là 5000N. Hỏi cần cầu năng được thùng hàng có khôi lượng (đơn vị kg) tồi đa là bao nhiêu (làm tròn đến hàng đơn vị)? Lây g =10 m/ s2
Trong 5 giây đầu tiên, một chất điểm chuyển động theo phương trình \[s\left( t \right) = - {t^3} + 6{t^2} + t + 5\], Trong đó \[t\] tính bằng giây và \[s\] tính bằng mét. Chất điểm có vận tốc tức thời lớn nhất bằng bao nhiêu trong 5 giây đầu tiên đó?
