Bộ 5 đề thi giữa kì 1 Toán 11 Kết nối tri thức cấu trúc mới (có tự luận) có đáp án - Đề 4
21 câu hỏi
Một chiếc đồng hồ có kim giờ \(OM\) chỉ số 12, kim phút \(ON\) chỉ số 3.
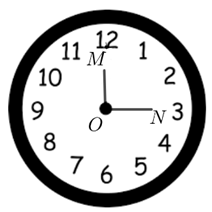
Số đo của góc lượng giác \(\left( {OM,ON} \right)\) là
\[ - \frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}\].
\[ - \frac{{3\pi }}{2} + k2\pi ,k \in \mathbb{Z}\].
\[\pi + k2\pi ,k \in \mathbb{Z}\].
\[\frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}\].
Cho \(\cos \alpha = \frac{1}{3}\). Khi đó \(\sin \left( {\alpha - \frac{{3\pi }}{2}} \right)\) bằng
\( - \frac{1}{3}.\)
\(\frac{2}{3}.\)
\( - \frac{2}{3}.\)
\(\frac{1}{3}.\)
Cho hàm số \(y = \cos x\) có đồ thị như hình vẽ dưới đây:

Hàm số \(y = \cos x\) đồng biến trên khoảng nào dưới đây?
\(\left( {0;\pi } \right)\).
\(\left( {\frac{{3\pi }}{2};\frac{{5\pi }}{2}} \right)\).
\(\left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right)\).
\(\left( { - 3\pi ; - 2\pi } \right)\).
Tìm nghiệm của phương trình \(\sin 2x = 1\).
\(x = \frac{\pi }{4} + k\pi {\rm{ }}\left( {k \in \mathbb{Z}} \right)\).
\(x = \frac{\pi }{4} + k2\pi {\rm{ }}\left( {k \in \mathbb{Z}} \right)\).
\(x = \frac{\pi }{2} + k2\pi {\rm{ }}\left( {k \in \mathbb{Z}} \right)\).
\(x = \frac{{k\pi }}{2}{\rm{ }}\left( {k \in \mathbb{Z}} \right)\).
Cho dãy số \(\left( {{u_n}} \right)\), biết \({u_n} = \frac{{2{n^2} - 1}}{{{n^2} + 3}}\). Tìm số hạng \({u_5}\).
\({u_5} = \frac{{17}}{{12}}.\)
\({u_5} = \frac{{71}}{{39}}.\)
\({u_5} = \frac{7}{4}.\)
\({u_5} = \frac{1}{4}.\)
Cho cấp số cộng \(\left( {{u_n}} \right)\) với \({u_n} = 5 - 2n\). Tìm công sai của cấp số cộng.
\(d = - 2\).
\(d = 1\).
\(d = 3\).
\(d = 2\).
Trong các dãy số \(\left( {{u_n}} \right)\)sau đây, dãy số nào là cấp số nhân?
\({u_n} = \frac{1}{n}\).
\({u_n} = 3n\).
\({u_n} = {2^n} + 1\).
\({u_n} = {2^n}\).
Khảo sát thời gian làm bài tập Toán của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:

Số học sinh được khảo sát là
\(25\).
\(26\).
\(27\).
\(28\).
Cho mẫu số liệu ghép nhóm về chiều cao của \[25\]cây dừa giống, như sau:
![Cho mẫu số liệu ghép nhóm về chiều cao của \[25\]cây dừa giống, như sau: Mốt của mẫu số liệu ghép nhóm này là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/blobid2-1757597535.png)
Mốt của mẫu số liệu ghép nhóm này là
\[{M_o} = \frac{{50}}{3}\].
\[{M_o} = \frac{{70}}{3}\].
\[{M_o} = \frac{{70}}{2}\].
\[{M_o} = \frac{{80}}{3}\].
Cho \(\cos x = \frac{1}{3}\left( { - \frac{\pi }{2} < x < 0} \right)\). Giá trị của \(\tan 2x\) là
\(\frac{{4\sqrt 2 }}{7}\).
\(\frac{{\sqrt 5 }}{2}\).
\( - \frac{{4\sqrt 2 }}{7}\).
\( - \frac{{\sqrt 5 }}{2}\).
Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ?
\(y = {\tan ^2}x\).
\(y = \cos 3x \cdot \sin x\).
\(y = \cos x + \sin x\).
\(y = \cos x \cdot {\sin ^2}x\).
Cho dãy số \(\left( {{u_n}} \right),\) biết \({u_n} = \frac{{2n + 5}}{{5n - 4}}.\)Số \(\frac{7}{{12}}\) là số hạng thứ bao nhiêu của dãy số?
8.
6.
9.
10.
Cho dãy số \(\left( {{u_n}} \right)\), biết \({u_1} = 8,{u_{n + 1}} = 4{u_n} - 9\) với \(n \in {\mathbb{N}^{\rm{*}}}\). Đặt \({v_n} = {u_n} - 3\) với \(n \in {\mathbb{N}^{\rm{*}}}\).
(a)\({v_1} = 5\).
(b) Dãy số \(\left( {{v_n}} \right)\) là một cấp số nhân có công bội \(q = - 3\).
(c) Công thức của số hạng tổng quát \({v_n}\) là \({v_n} = 5 \cdot {\left( { - 3} \right)^{n - 1}}\).
(d) Công thức của số hạng tổng quát \({u_n}\) là \({u_n} = 3 + 5 \cdot {\left( { - 3} \right)^{n - 1}}\).
Kết quả khảo sát cân nặng của 25 quả cam ở mỗi lô hàng \(A,B\) được cho ở bảng sau:

(a) Giá trị đại diện nhóm \(\left[ {150;155} \right)\) bằng 152,5.
(b) Nhóm chứa mốt của số liệu ở lô hàng \(A\) là \(\left[ {155;160} \right)\).
(c) Nhóm chứa mốt của số liệu ở lô hàng \(B\) là \(\left[ {160;165} \right)\).
(d) Theo số trung bình thì cam ở lô hàng \(B\) nặng hơn cam ở lô hàng \(A\).
Cho \[2\tan a - \cot a = 1\] với \[ - \frac{\pi }{2} < a < 0\]. Tính giá trị biểu thức \[P = \frac{{\tan \left( {6\pi - a} \right) - 2\cot \left( {3\pi + a} \right)}}{{3\tan \left( {\frac{{3\pi }}{2} + a} \right)}}\].
Biến đổi thành tổng biểu thức \(P = 4\sin 3x\sin 2x\cos x\) ta được
\(P = a\cos 2x + b\cos 4x + c\cos 6x + d\).
Tính \(a + b + c + d\).
Tìm giá trị nguyên lớn nhất của tham số \(m\) để dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{mn - 1}}{{n + 1}}\) là dãy số giảm.
Cho cấp số nhân \(\left( {{u_n}} \right)\) có \(\left\{ \begin{array}{l}{u_1} + {u_5} = 51\\{u_2} + {u_6} = 102\end{array} \right.\). Hỏi số \(12288\) là số hạng thứ bao nhiêu của cấp số nhân?
Nhiệt độ ngoài trời ở một thành phố vào các thời điểm khác nhau trong ngày có thể được mô phỏng bởi công thức \(h\left( t \right) = 31 + 3\sin \left[ {\frac{\pi }{{12}}\left( {t - 9} \right)} \right]\), với \(h\) tính bằng độ C và \(t\) là thời gian trong ngày tính bằng giờ \(\left( {0 < t \le 24} \right)\).
(a) Tính nhiệt độ ngoài trời ở thành phố đó vào lúc 19 giờ.
(b) Vào lúc mấy giờ trong ngày thì nhiệt độ ngoài trời ở thành phố đó là cao nhất?
Sinh nhật bạn của An vào ngày \[01\] tháng 05. An muốn mua một món quà sinh nhật cho bạn nên quyết định bỏ ống heo \[100\] đồng vào ngày \[01\] tháng \[01\] năm \[2025\], sau đó cứ liên tục ngày sau hơn ngày trước \[100\] đồng. Hỏi đến ngày sinh nhật của bạn, An đã tích lũy được bao nhiêu tiền? (thời gian bỏ ống heo tính từ ngày \[01\] tháng \[01\] năm \[2025\] đến ngày \[30\] tháng \[4\] năm \[2025\]).
[1D3-0Trong một hội thao, thời gian chạy 200 m của một nhóm vận động viên được ghi lại trong bảng sau:

Dựa vào bảng dữ liệu trên, ban tổ chức muốn chọn ra khoảng 50% số vận động viên chạy nhanh nhất để tiếp tục thi vòng 2. Ban tổ chức nên chọn các vận động viên có thời gian chạy không quá bao nhiêu giây?








