Bộ 5 đề thi giữa kì 1 Toán 11 Kết nối tri thức cấu trúc mới (có tự luận) có đáp án - Đề 2
21 câu hỏi
Cho \(\frac{{7\pi }}{4} < \alpha < 2\pi \). Khẳng định nào sau đây đúng?
\(\cos \alpha > 0\).
\(\sin \alpha > 0\).
\(\tan \alpha > 0\).
\(\cot \alpha > 0\).
Khẳng định nào dưới đây sai?
\(\cos 2a = 2\cos a - 1\).
\(2{\sin ^2}a = 1 - \cos 2a\).
\(\sin \left( {a + b} \right) = \sin a\cos b + \sin b\cos a\).
\(\sin 2a = 2\sin a \cdot \cos a\).
Mệnh đề nào dưới đây đúng?
Hàm số \(y = \cot x\) là hàm số chẵn.
Hàm số \(y = \sin x\) là hàm số chẵn.
Hàm số \(y = \tan x\) là hàm số chẵn.
Hàm số \(y = \cos x\) là hàm số chẵn.
Tìm nghiệm của phương trình \(\cos x = - \frac{1}{2}.\)
\(x = \pm \frac{\pi }{3} + k2\pi ,k \in \mathbb{Z}.\)
\(x = \pm \frac{{2\pi }}{3} + k2\pi ,k \in \mathbb{Z}.\)
\(x = \pm \frac{\pi }{6} + k2\pi ,k \in \mathbb{Z}.\)
\(x = \pm \frac{\pi }{6} + k\pi ,k \in \mathbb{Z}.\)
Cho dãy số \(\left( {{u_n}} \right)\) xác định bởi \(\left\{ \begin{array}{l}{u_1} = 2\\{u_{n + 1}} = \frac{1}{3}\left( {{u_n} + 1} \right)\end{array} \right..\) Tìm số hạng \({u_3}.\)
\({u_3} = \frac{5}{9}.\)
\({u_3} = 1.\)
\({u_3} = \frac{2}{3}.\)
\({u_3} = \frac{{14}}{{27}}.\)
Cho cấp số cộng \(\left( {{u_n}} \right)\), biết \({u_1} = 2,{u_2} = 8\). Công sai của cấp số cộng là
\(d = 10\).
\(d = 6.\)
\(d = 4.\)
\(d = 16.\)
Dãy số nào sau đây là cấp số nhân?
\(1\), \( - 2\), \(4\), \( - 8\), \( - 16\).
\(2\), \(22\), \(222\), \(22222\).
\(3\), \(6\), \(12\), \(24\).
\(x\), \(2x\), \(3x\), \(4x\) với \(x \ne 0\).
Mệnh đề nào sau đây đúng?
Tứ diện có 4 mặt và 6 cạnh.
Tứ diện có 4 mặt và 4 cạnh.
Tứ diện có 4 mặt và 5 cạnh.
Tứ diện có 4 cạnh và 6 mặt.
Cho hình lập phương \(ABCD.EFGH\). Mệnh đề nào sau đây sai?
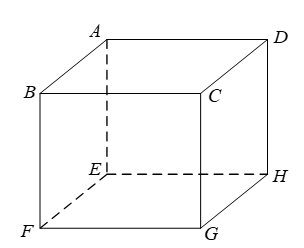
\(BG\) và \(HD\) chéo nhau.
\(BF\) và \(AD\) chéo nhau.
\(AB\) song song với \(HG\).
\(CG\) cắt \(HE\).
Biết \(\cos a = \frac{1}{3}\), \(\cos b = \frac{1}{4}\). Giá trị \[\cos \left( {a + b} \right) \cdot \cos \left( {a - b} \right)\] bằng
\[ - \frac{{113}}{{144}}.\]
\[ - \frac{{115}}{{144}}.\]
\[ - \frac{{117}}{{144}}.\]
\[ - \frac{{119}}{{144}}.\]
Cho cấp số cộng \(\left( {{u_n}} \right)\) biết \({u_1} = 4\) và \(d = 3\). Tổng \(S\) của \(20\) số hạng đầu tiên của cấp số cộng bằng bao nhiêu?
\({S_2}_0 = 750\).
\({S_2}_0 = 650\).
\({S_{20}} = 460\).
\({S_{20}} = 860\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành (xem hình vẽ). Khẳng định nào sau đây sai?
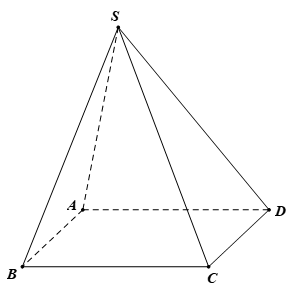
\(BC{\rm{//}}\left( {SAD} \right)\).
\(CD{\rm{//}}\left( {SAB} \right)\).
\(SA{\rm{//}}\left( {SCD} \right)\).
\(AD{\rm{//}}\left( {SBC} \right)\).
Cho hàm số \(y = \sin \left( {2x - \frac{\pi }{2}} \right)\).
(a) Tập xác định của hàm số đã cho là \(\left[ { - 1;1} \right]\).
(b) Hàm số đã cho là hàm số lẻ.
(c) Hàm số đã cho là hàm tuần hoàn với chu kì \(T = \pi \).
(d) Giá trị lớn nhất của hàm số đã cho trên \(\left[ {\frac{{ - \pi }}{8};\frac{\pi }{3}} \right]\) bằng \(1\).
Một kiến trúc sư thiết kế một hội trường với 15 ghế ngồi ở hàng thứ nhất, 18 ghế ngồi ở hàng thứ hai, 21 ghế ngồi ở hàng thứ ba, và cứ như vậy (số ghế ở hàng sau nhiều hơn 3 ghế so với số ghế ở hàng liền trước nó).
(a) Số ghế ở mỗi hàng lập thành một cấp số cộng.
(b) Số hạng đầu của dãy số là \(18\).
(c) Cấp số cộng có công sai \(d = 3\).
(d) Nếu muốn hội trường đó có sức chứa ít nhất 870 ghế ngồi thì kiến trúc sư đó phải thiết kế tối thiểu 15 hàng ghế.
Rút gọn biểu thức
\[A = \cos \left( {\alpha + 26\pi } \right) - 2\sin \left( {\alpha - 7\pi } \right) - \cos 1,5\pi - \cos \left( {\alpha + \frac{{2003\pi }}{2}} \right) + \cos \left( {\alpha - 1,5\pi } \right) \cdot \cot \left( {\alpha - 8\pi } \right)\]
ta được kết quả là \(a\sin \alpha + b\cos \alpha \)\(\left( {a,b \in \mathbb{Z}} \right)\). Khi đó \(3a + b\) bằng bao nhiêu?
Có bao nhiêu nghiệm của phương trình \(\sqrt 2 {\rm{cos}}\left( {x + \frac{\pi }{3}} \right) = 1\)thuộc đoạn \(\left[ {0;2\pi } \right]\)?
Một công ty phần mềm tuyển một chuyên gia về công nghệ thông tin với mức lương năm đầu tiên là \(300\) triệu đồng và cam kết tăng thêm \(5\% \) lương mỗi năm so với năm liền kề nếu hoàn thành tốt công việc được giao. Tính tổng số tiền lương mà chuyên gia đó nhận được sau khi làm việc cho công ty \(10\) năm biết rằng người đó luôn hoàn thành tốt công việc (làm tròn kết quả đến hàng đơn vị theo đơn vị triệu đồng).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\)là hình bình hành. Gọi \(M,N,P\) lần lượt là trung điểm của các đoạn thẳng \(BC,CD,SA\). Hình tạo bởi các giao tuyến của mặt phẳng \(\left( {MNP} \right)\) với các mặt của hình chóp \(S.ABCD\) là một đa giác có bao nhiêu cạnh?
Hằng ngày, mực nước của một con kênh lên xuống theo thuỷ triều. Độ sâu \(h\,\,{\rm{(m)}}\) của mực nước trong kênh tính theo thời gian \(t\) (giờ) trong một ngày \((0 \le t < 24)\) cho bởi công thức \(h = 3\cos \left( {\frac{{\pi t}}{6} + 1} \right) + 12\). Tìm \(t\) để độ sâu của mực nước là \(15{\rm{\;m}}\).
Một người nhảy bungee (một trò chơi mạo hiểm mà người chơi nhảy từ một nơi có địa thế cao xuống với dây đai an toàn buộc xung quanh người) từ một cây cầu và căng một sợi dây dài \(150{\rm{\;m}}\). Sau mỗi lần rơi xuống, nhờ sự đàn hồi của dây, người nhảy được kéo lên một quãng đường có độ dài bằng \(60\% \) so với lần rơi trước đó và lại bị rơi xuống đúng bằng quãng đường vừa được kéo lên (Hình vẽ).
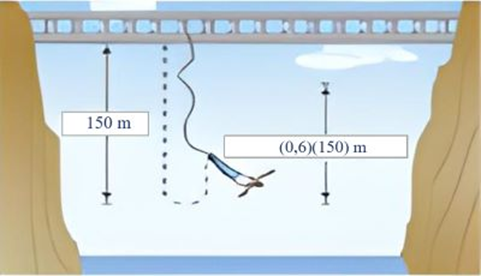
Tính tổng quãng đường người đó đi được sau 15 lần kéo lên và lại rơi xuống.
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành tâm \[O\]. Gọi \(M\), \(N\) lần lượt là trung điểm của các cạnh \(SA\) và \(SC\).
(a)Chứng minh \[MN{\rm{//}}\left( {ABCD} \right).\]
(b) Gọi \[P\] là trung điểm \[BO\]. Xác định giao điểm \(Q\) của cạnh \(SD\) và mặt phẳng \(\left( {MNP} \right)\). Tính tỷ số \(\frac{{SQ}}{{SD}}\).








