Bộ 5 đề thi giữa kì 1 Toán 11 Kết nối tri thức cấu trúc mới có đáp án - Đề 5

Mệnh đề nào sau đây là sai?

Giá trị lớn nhất và giá trị nhỏ nhất của hàm số \[y = 3\sin 3x - 4\] lần lượt là

Nghiệm của phương trình \[\cos 3x = \cos \frac{\pi }{{15}}\] có nghiệm là

Nghiệm của phương trình \[\sqrt 3 \cot \left( {2x + \frac{\pi }{6}} \right) = 1\] là

Cho dãy số có các số hạng đầu là: \[\frac{1}{3};\frac{1}{{{3^2}}};\frac{1}{{{3^3}}};\frac{1}{{{3^4}}};\frac{1}{{{3^5}}};....\] Số hạng tổng quát của dãy số này là

Trong các dãy số sau, dãy nào không phải cấp số cộng?

Cho cấp số nhân \[\left( {{u_n}} \right)\], biết \[{u_1} = 2,{u_2} = 8\]. Công bội \[q\] của cấp số nhân đã cho là

Cho dãy số \[\left( {{u_n}} \right)\] biết \[{u_n} = \frac{{10}}{{{3^n}}}\]. Mệnh đề nào sau đây đúng?

Cho cấp số cộng \[\left( {{u_n}} \right)\] có \[{u_1} = 11\] và công sai \[d = 4\]. Hãy tính \[{u_{99}}\].

Cho mẫu số liệu về chiều cao (cm) của các học sinh nữ trong khối 11 của một trường như sau:

Mẫu số liệu trên có bao nhiêu số liệu, bao nhiêu nhóm?

Tìm hiểu thời gian xem tivi trong tuần trước (đơn vị: giờ) của một số học sinh thu được kết quả sau:

Giá trị đại diện của nhóm \[\left[ {15;20} \right)\] là:

Phần II. Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu hỏi, học sinh chọn Đúng hoặc Sai.

 Cho hàm số \[y = \cot x\]. Xét tính đúng – sai của các phát biểu sau:

a) \[y = \cot x\] là hàm số lẻ, đồ thị đối xứng qua trục tung.

b) Đồ thị hàm số \[y = \cot x\] có dạng:

c) Đồ thị hàm số \[y = \cot x\] cắt trục hoành tại 3 điểm có hoành độ trong khoảng \[\left( {0;2\pi } \right).\]

d) Tổng các nghiệm của phương trình \[\cot x = \sqrt 3 \] trong khoảng \[\left( {0;2\pi } \right)\] là \[\frac{{3\pi }}{2}\].

Một vật dao động xung quanh vị trí cân bằng theo phương trình \[x = 1,5\cos \left( {\frac{{\pi t}}{4}} \right)\] trong đó \[t\] là thời gian được tính bằng giây và quãng đường \[h = \left| x \right|\] được tính bằng mét là khoảng cách theo phương ngang của chất điểm đối với vị trí cân bằng. Xét tính đúng sai của các khẳng định sau:

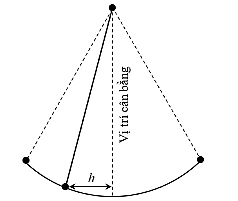
a) Vật ở xa vị trí cân bằng nhất nghĩa là \[h = 1,5{\rm{ m}}\].

b) Trong 10 giây đầu tiên, có ba thời điểm vật ở xa vị trí cân bằng nhất.

c) Khi vật ở vị trí cân bằng thì \[\cos \left( {\frac{{\pi t}}{4}} \right) = 0\].

d) Trong khoảng từ \[0\] đến \[20\] giây thì vật qua vị trí cân bằng 5 lần.

Một sinh viên sau khi ra trường và xin vào làm cho một trung tâm với mức lương khởi điểm là \[100\] triệu đồng một năm. Cứ sau mỗi năm, trung tâm trả thêm cho sinh viên \[20\] triệu đồng. Gọi \[{u_n}\] (triệu đồng) là số tiền lương mà sinh viên đó nhận được ở năm thứ \[n\]. Xét tính đúng sai của các khẳng định sau:

a) Số tiền lương sinh viên nhận được ở năm thứ hai là \[120\] triệu đồng.

b) Số tiền lương sinh viên nhận được ở năm thứ 10 là \[300\] triệu đồng.

c) Dãy số \[\left( {{u_n}} \right)\] là cấp số cộng có \[{u_1} = 120\] và công sai \[d = 20\].

d) Giả sử, mỗi năm bạn sinh biên chi tiêu tiết kiệm \[70\] triệu đồng. Vậy sau ít nhất \[12\] năm thì sinh viên đó mua được căn chung cư \[2\] tỉ đồng.

Kết quả điều tra về số giờ làm thêm trong một tuần của sinh viên một trường đại học X được cho bởi bảng sau:

a) Số sinh viên được điều tra là \[100\].

b) Số giờ làm thêm trung bình của mỗi sinh viên trường đại học X không ít hơn \[6\] giờ.

c) Số trung vị của mẫu số liệu trên bằng \[7,5\].

d) Tứ phân vị thứ nhất của mẫu số liệu trên bằng \[6,5\].

Phần III. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 1 đến câu 6.

Cho cấp số nhân \[\left( {{u_n}} \right)\] thỏa mãn \[\left\{ \begin{array}{l}{u_1} + {u_5} = 51\\{u_2} + {u_6} = 102\end{array} \right.\]. Tính tích của số hạng đầu \[{u_1}\] và công bội \[q\].

Tập hợp các giá trị của tham số \[m\] để phương trình \[\sin 2x + 2 = m\] có nghiệm là \[\left[ {a;b} \right]\]. Khi đó tính giá trị \[T = a + 2b\].

Giả sử một vật dao động điều hòa xung quanh vị trí cân bằng theo phương trình \[x = 2\cos \left( {5t - \frac{\pi }{6}} \right)\]. Ở đây, thời gian \[t\] tính bằng giây và quãng đường \[x\] tính bằng centimét, vật đi qua vị trí cân bằng bao nhiêu lần trong 3 giây đầu?

Một loại vi khuẩn sau mỗi phút số lượng được tăng gấp đôi biết rằng sau 5 phút người ta đếm được 64000 con. Hỏi sau bao nhiêu phút thì có được 2048000 con?

Một đa giác có \[n\] cạnh và có chu vi bằng \[158{\rm{ cm}}\]. Biết số đo các cạnh của đa giác lập thành một cấp số cộng và công sai \[d = 3{\rm{ cm}}\] và cạnh lớn nhất có độ dài là \[44{\rm{ cm}}\]. Đa giác đó có bao nhiêu cạnh?

Khi đo cân nặng của học sinh lớp 11D, ý tá lập được bảng số liệu ghép nhóm sau đây:

Tứ phân vị thứ nhất của mẫu số liệu của học sinh lớp 11D bằng bao nhiêu? (Kết quả được làm tròn đến hàng phần chục).