Bộ 5 đề thi giữa kì 1 Toán 11 Kết nối tri thức cấu trúc mới có đáp án - Đề 4
22 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, học sinh chỉ chọn một phương án
Đổi số đo góc \(105^\circ \) sang radian bằng
\(\frac{{5\pi }}{{12}}.\)
\(\frac{{7\pi }}{{12}}.\)
\(\frac{{9\pi }}{{12}}.\)
\(\frac{{5\pi }}{8}.\)
Trong các hệ thức sau, hệ thức nào đúng?
\({\sin ^2}x + {\cos ^2}x = 1.\)
\(\sin {x^2} + \cos {x^2} = 1.\)
\(\sin 2x + \cos 2x = 1.\)
\({\sin ^2}x + \cos 2x = 1.\)
Tập xác định của hàm số \(y = \tan x\) là
\(x \ne \frac{\pi }{2} + k\pi ,{\rm{ }}k \in \mathbb{Z}.\)
\(x \ne \frac{\pi }{2} + k2\pi ,{\rm{ }}k \in \mathbb{Z}.\)
\(x \ne - \frac{\pi }{2} + k2\pi ,{\rm{ }}k \in \mathbb{Z}.\)
\(x \ne k\pi ,{\rm{ }}k \in \mathbb{Z}.\)
Nghiệm của phương trình \(2\cos x + \sqrt 3 = 0\) là
\(x = \pm \frac{{5\pi }}{6} + k2\pi ,{\rm{ }}k \in \mathbb{Z}.\)
\(x = \pm \frac{\pi }{6} + k\pi ,{\rm{ }}k \in \mathbb{Z}.\)
\(x = \pm \frac{\pi }{6} + k2\pi ,{\rm{ }}k \in \mathbb{Z}.\)
\(x = \pm \frac{{5\pi }}{6} + k\pi ,{\rm{ }}k \in \mathbb{Z}.\)
Số giá trị nguyên của tham số \(m\) để phương trình \(\sqrt 3 \cos x + m - 1 = 0\) có nghiệm là
\(1.\)
\(2.\)
\(3.\)
\(4.\)
Cho dãy số \(\left( {{u_n}} \right)\) có \({u_n} = \frac{{2n + 1}}{{n - 1}}.\) Tính \({u_8}\).
\({u_8} = \frac{{17}}{7}.\)
\({u_8} = 2.\)
\({u_8} = \frac{{15}}{7}.\)
\({u_8} = \frac{{16}}{7}.\)
Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} = - 0,1\) và công sai \(d = 4\). Số hạng thứ 7 của cấp số cộng này là
\(24.\)
\(24,1.\)
\(23,9.\)
\( - 23,9.\)
Cho cấp số nhân \(\left( {{u_n}} \right)\) với \({u_1} = - 2;{\rm{ q}} = - 5\). Viết bốn số hạng đầu tiên của cấp số nhân này ta được
\( - 2;10;50; - 250.\)
\( - 2;10; - 50;250.\)
\( - 2; - 10; - 50; - 250.\)
\( - 2;10;50;250.\)
Cho cấp số nhân có \({u_1} = - 8;{\rm{ q}} = \frac{3}{2}\). Số \( - \frac{{2187}}{{16}}\) là số hạng thứ mấy của cấp số này?
Thứ 8.
Thứ 9.
Thứ 7.
Không phải số hạng của cấp số nhân trên.
Cho cấp số cộng \(\left( {{u_n}} \right)\) với \({u_1} = - 6;{\rm{ }}d = 4\). Tổng 14 số hạng đầu tiên của cấp số cộng đó là
\({S_{14}} = 46.\)
\({S_{14}} = 308.\)
\({S_{14}} = 644.\)
\({S_{14}} = 280.\)
Điều tra về chiều cao của học sinh khối lớp 11, ta được mẫu số liệu sau:
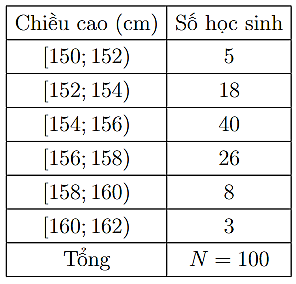
Mẫu số liệu ghép nhóm đã cho có tất cả bao nhiêu nhóm?
\(5.\)
\(6.\)
\(7.\)
\(12.\)
Tìm hiểu thời gian xem tivi trong tuần trước của một số học sinh thu được kết quả như sau (đơn vị: giờ):

Giá trị đại diện của nhóm \(\left[ {20;25} \right)\) là
\(22,5.\)
\(23.\)
\(20.\)
\(5.\)
Phần II. Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu hỏi, học sinh chọn Đúng hoặc Sai.
Hằng ngày, mặt trời chiếu vào bóng của một tòa chung cư cao \[40{\rm{ m}}\] in trên mặt đất, độ dài bóng của tòa nhà này được tính bằng công thức \[S\left( t \right) = 40\left| {\cot \frac{\pi }{{12}}t} \right|\], ở đó \[S\] được tính bằng mét, còn \[t\] là số giờ tính từ \[6\] giờ sáng.
a) Thời điểm \[8\] giờ sáng thì độ dài bóng của tòa nhà là \[40\sqrt 3 {\rm{ m}}\].
b) Thời điểm \[12\] giờ trưa thì độ dài bóng của tòa nhà là \[\frac{{20\sqrt 3 }}{3}{\rm{ m}}\].
c) Thời điểm \[3\] giờ \[45\] chiều thì độ dài bóng của tòa nhà lớn hơn độ dài tòa nhà khoảng \[10{\rm{ m}}{\rm{.}}\]
d) Thời điểm \[9\] giờ sáng hoặc \[3\] giờ chiều thì bóng của tòa nhà có độ dài bằng tòa nhà đó.
Cho hàm số \[y = 3 - \sin \left( {2x + \frac{\pi }{4}} \right)\]. Xét tính đúng sai của các khẳng định sau:
a) Hàm số có tập xác định \[D = \mathbb{R}.\]
b) Giá trị nhỏ nhất của hàm số bằng \[2\].
c) Giá trị lớn nhất của hàm số bằng \[4\].
d) Để phương trình \[3 - \sin \left( {2x + \frac{\pi }{4}} \right) = \frac{{\sqrt 3 m}}{2}\] có nghiệm thì \[m \in \left[ {a;b} \right]\]. Khi đó, giá trị \[T = a.b = \frac{{32}}{3}.\]
Giá của một chiếc ô tô lúc mới mua là \[680\] triệu đồng. Cứ sau mỗi năm sử dụng, giá của chiếc xe ô tô giảm \[50\] triệu đồng. Gọi \[{u_n}\] (triệu đồng) là giá của chiếc ô tô trong năm thứ \[n\] sử dụng.
a) \[{u_2} = 630.\]
b) Giá tiền của chiếc ô tô qua các năm lập thành một cấp số cộng với công sai \[d = 50.\]
c) Giá của chiếc ô tô sau 3 năm sử dụng lớn hơn \[500\] triệu đồng.
d) Sau ít nhất 8 năm sử dụng thì giá của chiếc ô tô nhỏ hơn một nửa giá ban đầu của nó.
Khảo sát thời gian chơi điện tử trong một ngày của một số học sinh lớp 11 thu được mẫu số liệu sau:

a) Giá trị đại diện của nhóm \[\left[ {60;80} \right)\] là \[70\].
b) Nhóm \[\left[ {20;40} \right)\] có tần số là \[14.\]
c) Nhóm chứa trung vị là \[\left[ {40;60} \right).\]
d) Thời gian trung bình chơi điện tử của các em học sinh lớp 11 là \[50\] phút.
Phần III. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 1 đến câu 6.
Cho cấp số nhân \[\left( {{u_n}} \right)\]có \[{u_1} = 3\] và \[q = 2\].
Tính tổng \[{S_{10}} = {u_1} + {u_2} + {u_3} + ... + {u_{10}}\].
Tập giá trị của hàm số \[y = \sin x + \sqrt 3 \cos x + 3\] có dạng \[\left[ {m;M} \right]\]. Tính giá trị \[m.M\].
Chiều cao \[h\left( m \right)\] của một cano trên vòng quay vào thời điểm \[t\] giây sau khi bắt đầu chuyển động được cho bởi công thức \[h\left( t \right) = 30 + 20\sin \left( {\frac{\pi }{{25}}t - \frac{\pi }{3}} \right)\]. Sau bao nhiêu giây thì cano đạt độ cao \[50\] m lần đầu tiên? (Kết quả làm tròn đến hàng phần chục).
Cho bốn số tạo thành một cấp số cộng có tổng bằng \[28\] và tổng các bình phương của chúng bằng \[276\]. Tìm tích của bốn số đó.
Chị Mai gửi tiền tiết kiệm vào ngân hàng theo hình thức lãi kép như sau: lần đầu chị gửi \[100\] triệu đồng. Sau đó, cứ hết một tháng chị lại gửi thêm vào ngân hàng \[6\] triệu đồng. Biết lãi suất của ngân hàng là \[0,5\% \] một tháng. Gọi \[{P_n}\] (triệu đồng) là số tiền chị có trong ngân hàng sau \[n\] tháng. Tính \[{P_5}\] (Kết quả được làm tròn đến hàng đơn vị).
Kết quả khảo sát hàm lượng vitamin C của một số loại trái cây cho bảng sau:

Hãy tìm trung vị của mẫu số liệu ghép nhóm trên.








