Bộ 5 đề thi giữa kì 1 Toán 11 Kết nối tri thức cấu trúc mới có đáp án - Đề 3
22 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, học sinh chỉ chọn một phương án
Chu kì của hàm số \[y = \cos x\] là
\[\frac{\pi }{2}.\]
\[\pi .\]
\[2\pi .\]
\[k2\pi .\]
Cho \[\sin x = \frac{4}{5}\] với \[\frac{\pi }{2} < x < \pi \]. Giá trị của \[\cos x\] bằng
\[\frac{1}{5}.\]
\[\frac{3}{5}.\]
\[ - \frac{3}{5}.\]
\[\frac{4}{5}.\]
Xác định số đo của góc lượng giác \[\left( {Ou,Ov} \right)\] được biểu diễn trong hình bên dưới đây
![Hướng dẫn giải Đáp án đúng là: A Ta có: \[\left( {Ou,Ov} \right) = - \left( {360^\circ - 60^\circ } \right) = - 300^\circ \]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/16-1760769264.png)
\[ - 300^\circ .\]
\[510^\circ .\]
\[60^\circ .\]
\[ - 420^\circ .\]
Tập xác định của hàm số \[y = \frac{{\sin x}}{{1 - \cos x}}\] là
\[D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}.\]
\[D = \mathbb{R}\backslash \left\{ {k\pi |k \in \mathbb{Z}} \right\}.\]
\[D = \mathbb{R}\backslash \left\{ {k2\pi |k \in \mathbb{Z}} \right\}.\]
\[D = \mathbb{R}\backslash \left\{ {\frac{{k\pi }}{2}|k \in \mathbb{Z}} \right\}.\]
Nghiệm của phương trình \[2\sin x - \sqrt 3 = 0\] là
\[\left[ \begin{array}{l}x = \frac{\pi }{3} + k2\pi \\x = \frac{{2\pi }}{3} + k2\pi \end{array} \right.,{\rm{ }}k \in \mathbb{Z}.\]
\[\left[ \begin{array}{l}x = \frac{\pi }{6} + k2\pi \\x = \frac{{5\pi }}{6} + k2\pi \end{array} \right.,{\rm{ }}k \in \mathbb{Z}.\]
\[x = \pm \frac{\pi }{6} + k2\pi ,{\rm{ }}k \in \mathbb{Z}.\]
\[x = \pm \frac{\pi }{2} + k2\pi ,{\rm{ }}k \in \mathbb{Z}.\]
Dãy số \[\left( {{u_n}} \right)\] là dãy số giảm khi và chỉ khi
\[{u_n} < {u_{n + 1}},{\rm{ }}\forall n \in {\mathbb{N}^ * }.\]
\[{u_n} \le {u_{n + 1}},{\rm{ }}\forall n \in {\mathbb{N}^ * }.\]
\[{u_n} > {u_{n + 1}},{\rm{ }}\forall n \in {\mathbb{N}^ * }.\]
\[{u_n} \ge {u_{n + 1}},{\rm{ }}\forall n \in {\mathbb{N}^ * }.\]
Cho cấp số nhân \[\left( {{u_n}} \right)\] có \[{u_1} = 3\] và \[q = - 2\]. Số \[192\] là số hạng thứ mấy của cấp số nhân trên?
\[6.\]
\[5.\]
\[8.\]
\[7.\]
Cho cấp số cộng \[\left( {{u_n}} \right)\] có \[{u_1} = 1\] và công sai \[d = 2\]. Tổng 10 số hạng đầu tiên của dãy là
\[{S_{10}} = 110.\]
\[{S_{10}} = 100.\]
\[{S_{10}} = 21.\]
\[{S_{10}} = 19.\]
Hình chóp tứ giác có tất cả bao nhiêu mặt là tam giác?
\[6.\]
\[3.\]
\[4.\]
\[5.\]
Cho tứ diện \[ABCD\] như hình bên. Mệnh đề nào sau đây là đúng?
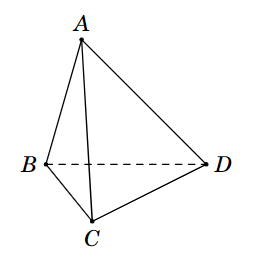
\[AB\] và \[CD\] cắt nhau.
\[BD\] và \[AC\] cắt nhau.
\[BD\] và \[AC\] chéo nhau.
\[CB\] và \[AD\] song song.
Cho hình chóp tứ giác \[S.ABCD\] có đáy \[ABCD\] là hình bình hành . Gọi \[I,J\] lần lượt là trung điểm của \[SA\] và \[SB\]. Khẳng định nào sau đây là sai?
\[\left( {SAB} \right) \cap \left( {IBC} \right) = IB.\]
\[CDIJ\]là hình thang.
\[\left( {SBD} \right) \cap \left( {JCD} \right) = JD.\]
\[\left( {IAC} \right) \cap \left( {IBD} \right) = AO\] (\[O\] là tâm \[ABCD\]).
Cho hình chóp \[S.ABCD\] có đáy là hình bình hành. Gọi \[M,N\] lần lượt là trung điểm của \[AD\] và \[BC\]. Giao tuyến của \[\left( {SMN} \right)\] và \[\left( {SAC} \right)\] là
\[SK\] với \[K\] là trung điểm của \[AB.\]
\[SO\] với \[O\] là tâm của hình bình hành \[ABCD.\]
\[SF\] với \[F\] là trung điểm của \[CD.\]
\[SD.\]
Phần II. Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu hỏi, học sinh chọn Đúng hoặc Sai.
Cho phương trình lượng giác \[2\sin x - \sqrt 2 = 0\]. Khi đó:
a) Phương trình tương đương với phương trình \[\sin x = \sin \frac{\pi }{4}.\]
b) Phương trình có nghiệm là \[x = \frac{\pi }{4} + k2\pi ;x = \frac{{3\pi }}{4} + k2\pi {\rm{ }}\left( {k \in \mathbb{Z}} \right).\]
c) Phương trình có nghiệm âm lớn nhất là \[ - \frac{\pi }{4}\].
d) Số nghiệm của phương trình trong khoảng \[\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\] là hai nghiệm.
Chiều cao so với mực nước biển trung bình tại các thời điểm \[t\] (giây) của mỗi cơn sóng được cho bởi hàm số \[h\left( t \right) = 75\sin \left( {\frac{{\pi t}}{8}} \right)\], trong đó \[h\left( t \right)\] được tính bằng centimét. (Tất cả các kết quả được làm tròn đến hàng phần mười).
a) Chiều cao của sóng tại thời điểm 5 giây bằng \[69,3{\rm{ }}\left( {cm} \right)\].
b) Chiều cao của sóng tại thời điểm 20 giây bằng \[{\rm{75 }}\left( {cm} \right)\].
c) Trong 30 giây đầu tiên (kể từ mốc \[t = 0\] giây), thời điểm để sóng đạt chiều cao lớn nhất là 6 giây.
d) Trong 30 giây đầu tiên (kể từ mốc \[t = 0\] giây), thời điểm để sóng đạt chiều cao lớn nhất là 18 giây.
Ông Minh gửi số tiền \[100\] triệu đồng vào một ngân hàng với hình thức lãi kép kì hạn 12 tháng với lãi suất \[7\% \]/ năm. Trong khoảng thời gian gửi tiền ông Minh không rút tiền ra và lãi suất không thay đổi. Khi đó:
a) Sau năm thứ nhất, số tiền ông Minh có là \[107\] triệu đồng.
b) Sau năm thứ hai, số tiền ông Minh nhận được là \[117\] triệu đồng.
c) Số tiền mà ông Minh nhận được sau \[n\] năm là số hạng thứ \[n\] của một cấp số nhân có số hạng đầu \[{u_1} = 107\] và công bội \[q = 1,7\].
d) Sau 10 năm, số tiền ông Minh nhận được lớn hơn \[195\] triệu đồng.
Cho hình chóp \[S.ABCD\], đáy là tứ giác \[ABCD\]. Biết \[AB\] cắt \[CD\] tại \[E\], \[AC\] cắt \[BD\] tại \[F\] trong mặt phẳng đáy. Xét tính đúng sai của các khẳng định sau:
a) Đường thẳng \[FE\] nằm trong mặt phẳng \[\left( {ABCD} \right).\]
b) \[AB\] là giao tuyến của hai mặt phẳng \[\left( {SAB} \right)\] và \[\left( {ABCD} \right).\]
c) \[SF\] là giao điểm của hai mặt phẳng \[\left( {SAB} \right)\] và \[\left( {SCD} \right)\], \[SE\] là giao tuyến của hai mặt phẳng \[\left( {SAC} \right)\] và \[\left( {SBD} \right).\]
d) Gọi \[G = FE \cap AD\]. Khi đó, \[SG\] là giao tuyến của mặt phẳng \[\left( {SFE} \right)\] và mặt phẳng \[\left( {SAD} \right)\].
Phần III. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 1 đến câu 6.
Tìm m để giá trị lớn nhất của hàm số \[y = 3\sin x + 4\cos x + m\] bằng \[10.\]
Cho biết bốn số \[5;x;15;y\] lập thành một cấp số cộng. Tính giá trị của biểu thức \[T = 3x + 2y\].
Cho hình chóp \[S.ABCD\] đáy là hình bình hành tâm \[O\]. Điểm \[M\] thuộc cạnh \[SB\]. Biết \[OM\parallel SD\]. Lấy \[I \in SA\] sao cho \[MI\parallel AB\]. Tính tỉ số của \[\frac{{MI}}{{CD}}\].
Một cây cầu có dạng cung \[OA\] là một phần của đồ thị hàm số \[y = 4,8\sin \frac{x}{5}\] và được mô tả trong hệ trục tọa độ với đơn vị trục là mét như hình bên.
![Một cây cầu có dạng cung \[OA\] là một phần của đồ thị hàm số \[y = 4,8\sin \frac{x}{5}\] và được mô tả trong hệ trục tọa độ vớ (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/20-1760769764.png)
Giả sử chiều rộng của con sông là đoạn thẳng \[OA\]. Tính chiều rộng của cây cầu đó. (Làm tròn kết quả đến hàng phần mười).
Một hội trường lớn có 35 ghế ở hàng đầu, 37 ghế ở hàng thứ hai, 39 ghế ở hàng thứ ba và cứ tiếp tục theo quy luật như vậy. Có tất cả 27 hàng ghế. Tính số ghế có ở hội trường đó.
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình bình hành. Gọi \[G\] là trọng tâm tam giác \[ABC\] và \[M\] là trung điểm \[SC\]. Gọi \[K\] là giao điểm của \[SD\] và mặt phẳng \[\left( {AGM} \right)\]. Tính tỉ số \[\frac{{KS}}{{KD}}\].








