Bộ 5 đề thi giữa kì 1 Toán 11 Kết nối tri thức cấu trúc mới có đáp án - Đề 2
22 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, học sinh chỉ chọn một phương án
Số đo theo đơn vị radian của góc \[315^\circ \] là
\[\frac{{7\pi }}{2}.\]
\[\frac{{7\pi }}{4}.\]
\[\frac{{2\pi }}{7}.\]
\[\frac{{4\pi }}{7}.\]
Biết rằng \[\sin x = \frac{1}{2}\] với \[90^\circ < x < 180^\circ \] thì
\[x = 30^\circ .\]
\[x = 60^\circ .\]
\[x = 120^\circ .\]
\[x = 150^\circ .\]
Trong các khẳng định sau, khẳng định nào là đúng?
\[\sin \left( {a - b} \right) = \sin a\sin b - \cos a\cos b.\]
\[\sin \left( {a - b} \right) = \sin a\cos b + \cos a\sin b.\]
\[\sin \left( {a + b} \right) = \sin a\cos b - \cos a\sin b.\]
\[\sin \left( {a + b} \right) = \sin a\cos b + \cos a\sin b.\]
Tập xác định của hàm số \[y = \cot x\] là
\[T = \mathbb{R}.\]
\[T = \mathbb{R}\backslash \left\{ 0 \right\}.\]
\[T = \mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}.\]
\[T = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}.\]
Phương trình \[\cot x + \sqrt 3 = 0\] có nghiệm là
\[x = \frac{\pi }{3} + k2\pi {\rm{ }}\left( {k \in \mathbb{Z}} \right).\]
\[x = \frac{\pi }{6} + k\pi {\rm{ }}\left( {k \in \mathbb{Z}} \right).\]
\[x = - \frac{\pi }{6} + k2\pi {\rm{ }}\left( {k \in \mathbb{Z}} \right).\]
\[x = - \frac{\pi }{6} + k\pi {\rm{ }}\left( {k \in \mathbb{Z}} \right).\]
Dãy số \[\left( {{u_n}} \right)\] là dãy số tăng khi và chỉ khi
\[{u_n} < {u_{n + 1}},{\rm{ }}\forall n \in {\mathbb{N}^ * }.\]
\[{u_n} > {u_{n + 1}},{\rm{ }}\forall n \in {\mathbb{N}^ * }.\]
\[{u_n} \ge {u_{n + 1}},{\rm{ }}\forall n \in {\mathbb{N}^ * }.\]
\[{u_n} \le {u_{n + 1}},{\rm{ }}\forall n \in {\mathbb{N}^ * }.\]
Cho cấp số nhân \[\left( {{u_n}} \right)\], biết \[{u_1} = - 2\] và \[{u_5} = - 162\]. Công bội \[q\] bằng
\[q = \pm 3.\]
\[q = - 3.\]
\[q = 81.\]
\[q = 3.\]
Cho cấp số cộng \[\left( {{u_n}} \right)\] có \[\left\{ \begin{array}{l}6{u_1} + 5{u_5} = 28\\{S_4} = 14\end{array} \right.\]. Số hạng \[{u_1}\] của cấp số cộng bằng:
\[{u_1} = 6.\]
\[{u_1} = 2.\]
\[{u_1} = - 3.\]
\[{u_1} = 8.\]
Trong các hình sau
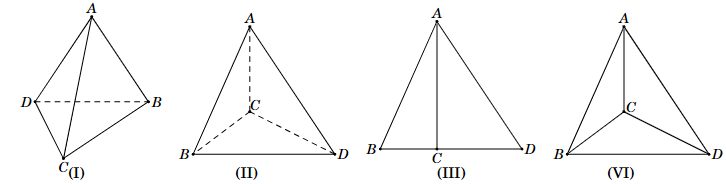
Hình nào có thể là hình biểu diễn một tứ diện?
\[\left( I \right).\]
\[\left( I \right),\left( {II} \right).\]
\[\left( I \right),\left( {II} \right),\left( {IV} \right).\]
\[\left( I \right),\left( {II} \right),\left( {III} \right),\left( {IV} \right).\]
Cho hình tứ diện \[ABCD\]. Giao tuyến của hai mặt phẳng \[\left( {ABC} \right)\] và \[\left( {CDA} \right)\] là đường thẳng.
\[AC.\]
\[CD.\]
\[AB.\]
\[BD.\]
Cho tứ diện \[ABCD\]. Gọi \[M,N\] lần lượt là trung điểm của \[BA,BC\]. Trong các đường thẳng sau, đường nào song song với \[MN\]?
\[AC.\]
\[CD.\]
\[AB.\]
\[BD.\]
Cho tứ diện \[ABCD\]. Gọi \[M,N\] lần lượt là trung điểm của \[AC,CD\]. Giao tuyến của hai mặt phẳng \[\left( {MBD} \right)\] và \[\left( {ABN} \right)\] là
Đường thẳng \[MN.\]
Đường thẳng \[AM.\]
Đường thẳng \[BG\] (\[G\] là trọng tâm tam giác \[ACD\]).
Đường thẳng \[AH\] (\[H\] là trực tâm tam giác \[ACD\]).
Phần II. Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu hỏi, học sinh chọn Đúng hoặc Sai.
Cho phương trình lượng giác \[\sin 2x = - \frac{1}{2}\] (*). Khi đó:
a) Phương trình (*) tương đương \[\sin 2x = \sin \frac{\pi }{6}.\]
b) Trong khoảng \[\left( {0;\pi } \right)\] phương trình có ba nghiệm.
c) Trong khoảng \[\left( {0;\pi } \right)\] phương trình có nghiệm lớn nhất bằng \[\frac{{11\pi }}{{12}}\].
d) Tổng các nghiệm của phương trình trong khoảng \[\left( {0;\pi } \right)\] bằng \[\frac{{3\pi }}{2}\].
Số giờ có ánh sáng mặt trời của một thành phố A ở vĩ độ \[40^\circ \] Bắc trong ngày thứ \[t\] của một năm không nhuận được cho bởi hàm số
\[d\left( t \right) = 3\sin \left[ {\frac{\pi }{{182}}\left( {t - 80} \right)} \right] + 12\] với \[t \in \mathbb{Z}\] và \[0 < t \le 365\].
a) Tập giá trị của hàm số \[d\left( t \right)\] là \[\left[ {9;15} \right].\]
b) Thành phố A có đúng 12 giờ có ánh sáng mặt trời vào một ngày duy nhất trong năm.
c) Vào ngày thứ 353 trong năm thành phố A có đúng 9 giờ có ánh sáng mặt trời.
d) Vào ngày thứ 107 trong năm thành phố A có đúng 15 giờ có ánh sáng mặt trời.
Tương truyền rằng nhà vua Ấn Độ cho phép người phát minh ra bàn cờ vua được chọn phần thưởng tùy theo sở thích. Người đó xin nhà vua: “Bàn cờ có 64 ô, với ô thứ nhất thần xin nhận 1 hạt tóc, ô thứ hai thì gấp đôi ô thứ nhất, ô thứ 3 thì gấp đôi ô thứ hai, … cứ như vậy ô sau nhận số hạt thóc gấp đôi phần thưởng dành cho ô trước và thần xin nhận tổng số hạt thóc ở 64 ô”. Biết rằng khối lượng của 100 hạt thóc là 20 gam. Khi đó:
a) Số hạt tóc ở 64 ô là một cấp số nhân có \[{u_1} = 1\] và \[q = 2.\]
b) Số hạt thóc ở ô thứ 8 là \[{2^8}.\]
c) Tổng khối lượng thóc của 64 ô trên bàn cờ khoảng \[369\] tỉ tấn.
d) Giả sử người đó muốn chở số thóc ở trên 32 ô đầu tiên về bằng tàu thủy, biết rằng mỗi chuyến tàu chở tối đa 10 tấn hàng hóa. Khi đó, người đó cần chở tối thiểu 86 chuyến tàu để chở hết số thóc đó.
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình chữ nhật. Gọi \[I,J\] lần lượt là trung điểm của các cạnh \[AD,BC\] và \[G\] là trọng tâm của tam giác \[SAB\]. Khi đó:
a) Giao tuyến của hai mặt phẳng \[\left( {SAB} \right)\] và \[\left( {SCD} \right)\] là đường thẳng qua \[S\] và song song với \[AB\].
b) Giao tuyến của hai mặt phẳng \[\left( {SAC} \right)\] và \[\left( {SBD} \right)\] là đường thẳng qua \[S\] và song song với \[AC\].
c) Giao tuyến của hai mặt phẳng \[\left( {SAB} \right)\] và \[\left( {IGJ} \right)\] là đường thẳng qua \[G\] và song song với \[CD\].
d) Lấy \[M\] trên \[SD\] sao cho \[SM = \frac{2}{3}SD\], \[N\] trên \[SA\] sao cho \[NA = \frac{1}{3}SA.\] Giao tuyến của hai mặt phẳng \[\left( {GMN} \right)\] và \[\left( {GBC} \right)\] là đường thẳng qua \[G\] và song song với \[AD.\]
Phần III. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 1 đến câu 6.
Cho góc \[\alpha \] thỏa mãn \[\frac{\pi }{2} < \alpha < \pi \] và \[\sin \alpha = \frac{2}{3}\].
Tính \[P = \frac{{1 + \sin 2\alpha + \cos 2\alpha }}{{\sin \alpha + \cos \alpha }}.\] (Kết quả làm tròn đến hàng phần mười).
Cho cấp số nhân \[\left( {{u_n}} \right)\] thỏa mãn \[{S_2} = 4\] và \[{S_3} = 13\]. Tính giá trị \[{S_5}\] biết công bội \[q < 0.\] Kết quả làm tròn đến chữ số phần chục.
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình thang với \[AD\parallel BC\] và \[AD = 2BC\]. Gọi \[M\] là điểm trên cạnh \[SD\] thỏa mãn \[SM = \frac{1}{3}SD.\] Mặt phẳng \[\left( {ABM} \right)\] cắt cạnh bên \[SC\] tại điểm \[N\]. Tính tỉ số \[\frac{{SN}}{{SC}}.\]
Chiều cao \[h\left( m \right)\] của một cabin trên vòng quay vào thời điểm \[t\] giây sau khi bắt đầu chuyển động được cho bởi công thức \[h\left( t \right) = 30 + 20\sin \left( {\frac{{\pi t}}{{25}} + \frac{\pi }{3}} \right)\]. Sau bao nhiêu giây thì cabin đạt độ cao \[40{\rm{ }}m\] lần đầu tiên?
Trong một khán phòng có tất cả 30 dãy ghế, dãy đầu tiên có 15 ghế, các dãy liền sau nhiều hơn dãy liền trước đó 4 ghế, hỏi trong khán phòng đó có tất cả bao nhiêu ghế?
Cho tứ diện \[ABCD\]. Các điểm \[P,Q\] lần lượt là trung điểm của \[AB\] và \[CD\]; điểm \[R\] nằm trên cạnh \[BC\] sao cho \[BR = 2RC\]. Gọi \[S\] là giao điểm của mặt phẳng \[\left( {PQR} \right)\] và cạnh \[AD\]. Tính tỉ số \[\frac{{SA}}{{SD}}\].








