Bộ 5 đề thi giữa kì 1 Toán 11 Cánh diều cấu trúc mới (có tự luận) có đáp án - Đề 5
21 câu hỏi
A. TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Một chiếc đồng hồ có kim giờ \(OM\) chỉ số 12, kim phút \(ON\) chỉ số 3.
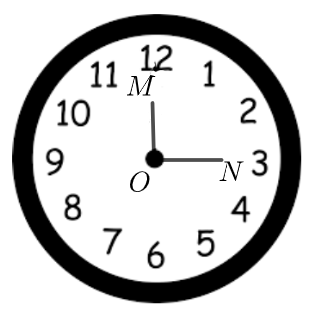
Số đo của góc lượng giác \(\left( {OM,ON} \right)\) là
\[ - \frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}\].
\[ - \frac{{3\pi }}{2} + k2\pi ,k \in \mathbb{Z}\].
\[\pi + k2\pi ,k \in \mathbb{Z}\].
\[\frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}\].
Cho \(\cos \alpha = \frac{1}{3}\). Khi đó \(\sin \left( {\alpha - \frac{{3\pi }}{2}} \right)\) bằng
\( - \frac{1}{3}.\)
\(\frac{2}{3}.\)
\( - \frac{2}{3}.\)
\(\frac{1}{3}.\)
Cho hàm số \(y = \cos x\) có đồ thị như hình vẽ dưới đây:
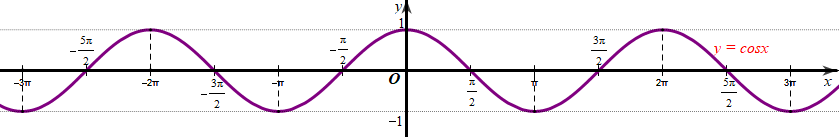
Hàm số \(y = \cos x\) đồng biến trên khoảng nào dưới đây?
\(\left( {0;\pi } \right)\).
\(\left( {\frac{{3\pi }}{2};\frac{{5\pi }}{2}} \right)\).
\(\left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right)\).
\(\left( { - 3\pi ; - 2\pi } \right)\).
Tìm nghiệm của phương trình \(\sin 2x = 1\).
\(x = \frac{\pi }{4} + k\pi {\rm{ }}\left( {k \in \mathbb{Z}} \right)\).
\(x = \frac{\pi }{4} + k2\pi {\rm{ }}\left( {k \in \mathbb{Z}} \right)\).
\(x = \frac{\pi }{2} + k2\pi {\rm{ }}\left( {k \in \mathbb{Z}} \right)\).
\(x = \frac{{k\pi }}{2}{\rm{ }}\left( {k \in \mathbb{Z}} \right)\).
Cho dãy số \(\left( {{u_n}} \right)\), biết \({u_n} = \frac{{2{n^2} - 1}}{{{n^2} + 3}}\). Tìm số hạng \({u_5}\).
\({u_5} = \frac{{17}}{{12}}.\)
\({u_5} = \frac{{71}}{{39}}.\)
\({u_5} = \frac{7}{4}.\)
\({u_5} = \frac{1}{4}.\)
Cho cấp số cộng \(\left( {{u_n}} \right)\) với \({u_n} = 5 - 2n\). Tìm công sai của cấp số cộng.
\(d = - 2\).
\(d = 1\).
\(d = 3\).
\(d = 2\).
Trong các dãy số \(\left( {{u_n}} \right)\)sau đây, dãy số nào là cấp số nhân?
\({u_n} = \frac{1}{n}\).
\({u_n} = 3n\).
\({u_n} = {2^n} + 1\).
\({u_n} = {2^n}\).
Cho hình chóp \(S.ABC\). Gọi \(M,N,K,E\) lần lượt là trung điểm của \(SA,SB,SC,BC\). Bốn điểm nào sau đây đồng phẳng?
\(M,N,K,C\).
\(M,N,K,E\).
\(M,K,A,C\).
\(M,N,A,C\).
Trong không gian, cho hai đường thẳng \[a\]và \[b\] không đồng phẳng. Khẳng định nào sau đây đúng?
\[a\] và \[b\] có thể song song với nhau.
\[a\] và \[b\] có ít nhất một điểm chung.
\[a\] và \[b\] không có điểm chung.
\[a\] và \[b\] có thể cắt nhau.
Cho \(\cos x = \frac{1}{3}\left( { - \frac{\pi }{2} < x < 0} \right)\). Giá trị của \(\tan 2x\) là
\(\frac{{4\sqrt 2 }}{7}\).
\(\frac{{\sqrt 5 }}{2}\).
\( - \frac{{4\sqrt 2 }}{7}\).
\( - \frac{{\sqrt 5 }}{2}\).
Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ?
\(y = {\tan ^2}x\).
\(y = \cos 3x \cdot \sin x\).
\(y = \cos x + \sin x\).
\(y = \cos x \cdot {\sin ^2}x\).
Cho dãy số \(\left( {{u_n}} \right),\) biết \({u_n} = \frac{{2n + 5}}{{5n - 4}}.\)Số \(\frac{7}{{12}}\) là số hạng thứ bao nhiêu của dãy số?
8.
6.
9.
10.
B. TRẮC NGHIỆM ĐÚNG - SAI. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho dãy số \(\left( {{u_n}} \right)\), biết \({u_1} = 8,{u_{n + 1}} = 4{u_n} - 9\) với \(n \in {\mathbb{N}^{\rm{*}}}\). Đặt \({v_n} = {u_n} - 3\) với \(n \in {\mathbb{N}^{\rm{*}}}\).
a)\({v_1} = 5\).
b) Dãy số \(\left( {{v_n}} \right)\) là một cấp số nhân có công bội \(q = - 3\).
c) Công thức của số hạng tổng quát \({v_n}\) là \({v_n} = 5 \cdot {\left( { - 3} \right)^{n - 1}}\).
d) Công thức của số hạng tổng quát \({u_n}\) là \({u_n} = 3 + 5 \cdot {\left( { - 3} \right)^{n - 1}}\).
Cho hình chóp \[S.ABCD\] có cạnh đáy \(ABCD\) là hình bình hành. Gọi \(H\) là trung điểm cạnh \(AB\),\(G\) trọng tâm tam giác \(SAB\). Lấy điểm \(M\) trên cạnh \(AD\), điểm\(N\) trên cạnh \(HC\) sao cho \(AD = 3AM,HC = 3HN\).
a) Giao tuyến của hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SHC} \right)\) là \(SH\).
b) Giao tuyến của mặt phẳng \(\left( {GMN} \right)\) và mặt phẳng \(\left( {SAB} \right)\) là đường thẳng đi qua \(G\) và song song với \(AD\).
c) Đường thẳng \(NG\) song song với mặt phẳng \(\left( {SCD} \right)\).
d) Gọi \(P\) là giao điểm của đường thẳng \(NG\) và mặt phẳng \(\left( {SAD} \right)\), khi đó tỉ lệ \(\frac{{PG}}{{GN}} = \frac{3}{4}\).
C. TRẢ LỜI NGẮN. Thí sinh trả lời câu 1 đến câu 4.
Cho \[2\tan a - \cot a = 1\] với \[ - \frac{\pi }{2} < a < 0\]. Tính giá trị biểu thức \[P = \frac{{\tan \left( {6\pi - a} \right) - 2\cot \left( {3\pi + a} \right)}}{{3\tan \left( {\frac{{3\pi }}{2} + a} \right)}}\].
Biến đổi thành tổng biểu thức \(P = 4\sin 3x\sin 2x\cos x\) ta được
\(P = a\cos 2x + b\cos 4x + c\cos 6x + d\).
Tính \(a + b + c + d\).
Tìm giá trị nguyên lớn nhất của tham số \(m\) để dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{mn - 1}}{{n + 1}}\) là dãy số giảm.
Cho cấp số nhân \(\left( {{u_n}} \right)\)có \(\left\{ \begin{array}{l}{u_1} + {u_5} = 51\\{u_2} + {u_6} = 102\end{array} \right.\). Hỏi số \(12288\) là số hạng thứ bao nhiêu của cấp số nhân?
PHẦN II. TỰ LUẬN
Nhiệt độ ngoài trời ở một thành phố vào các thời điểm khác nhau trong ngày có thể được mô phỏng bởi công thức \(h\left( t \right) = 31 + 3\sin \left[ {\frac{\pi }{{12}}\left( {t - 9} \right)} \right]\), với \(h\) tính bằng độ C và \(t\) là thời gian trong ngày tính bằng giờ \(\left( {0 < t \le 24} \right)\).
a) Tính nhiệt độ ngoài trời ở thành phố đó vào lúc 19 giờ.
b) Vào lúc mấy giờ trong ngày thì nhiệt độ ngoài trời ở thành phố đó là cao nhất?
Sinh nhật bạn của An vào ngày \[01\] tháng 05. An muốn mua một món quà sinh nhật cho bạn nên quyết định bỏ ống heo \[100\] đồng vào ngày \[01\] tháng \[01\] năm \[2025\], sau đó cứ liên tục ngày sau hơn ngày trước \[100\] đồng. Hỏi đến ngày sinh nhật của bạn, An đã tích lũy được bao nhiêu tiền? (thời gian bỏ ống heo tính từ ngày \[01\] tháng \[01\] năm \[2025\] đến ngày \[30\] tháng \[4\] năm \[2025\]).
Cho hình chóp \(S.ABCD,\)\(ABCD\) là hình thang cóng.| đáy là \(AD\) và \(BC,\)\(AD = 2BC.\) Gọi \(E\) là trung điểm \(SA,\)\(M\) là trọng tâm \(\Delta SAD,\)\(G\) là1m4| giao điểm của \(AC\) và \(BD.\)
a) Tìm giao tuyến của hai mặt phẳng \(\left( {MBC} \right)\) và \(\left( {SAD} \right).\)
b) Chứng minh \(MG\) song song với mặt phẳng \(\left( {SAB} \right)\).