Bộ 10 đề thi cuối kì 1 Toán 11 Cánh diều có đáp án - Đề 9
29 câu hỏi
Đổi số đo góc \(105^\circ \)sang radian
\(\frac{{7\pi }}{{12}}.\)
\(\frac{{9\pi }}{{12}}.\)
\(\frac{{5\pi }}{8}.\)
\(\frac{{5\pi }}{{12}}.\)
Cho \[\sin \alpha + \cos \alpha = \frac{1}{2}.\] Giá trị của \(\sin 2\alpha \) là
\( - \frac{3}{2}.\)
\(\frac{3}{2}.\)
\( - \frac{3}{4}.\)
\(\frac{3}{4}.\)
Giá trị lớn nhất của hàm số \(y = 2\sin x + 1\) bằng
\( - 1.\)
1.
\( - \frac{1}{2}.\)
3.
Đường cong trong hình vẽ bên dưới là đồ thị của một trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D. Hỏi hàm số đó là hàm số nào?
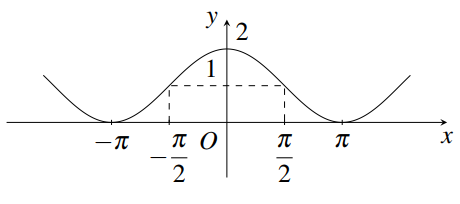
\(y = 1 + \cos x.\)
\(y = 2\cos x.\)
\(y = 2 - \sin x.\)
\(y = {\cos ^2}x + 1.\)
Tập nghiệm của phương trình \(\sin x = - 1\) là
\(S = \left\{ {\frac{\pi }{2} + k2\pi |k \in \mathbb{Z}} \right\}.\)
\(S = \left\{ { - \frac{\pi }{2} + k2\pi |k \in \mathbb{Z}} \right\}.\)
\(S = \left\{ {k2\pi |k \in \mathbb{Z}} \right\}.\)
\(S = \left\{ {\pi + k2\pi |k \in \mathbb{Z}} \right\}.\)
Cho dãy số \(\left( {{u_n}} \right)\) biết \({u_n} = \frac{{4n + 5}}{{n + 1}}\). Mệnh đề nào sau đây đúng về dãy số \(\left( {{u_n}} \right)?\)
Dãy số bị chặn.
Dãy số bị chặn trên.
Dãy số bị chặn dưới.
Không bị chặn.
Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} = - 3\) và \(d = \frac{1}{2}.\) Khẳng định nào sau đây đúng?
\({u_n} = - 3 + \frac{1}{2}\left( {n + 1} \right).\)
\({u_n} = - 3 + \frac{1}{2}n - 1.\)
\({u_n} = - 3 + \frac{1}{2}\left( {n - 1} \right).\)
\({u_n} = - 3 + \frac{1}{4}\left( {n - 1} \right).\)
Trong các dãy số sau, có bao nhiêu dãy số là cấp số cộng?
(I). Dãy số \(\left( {{u_n}} \right)\) với \({u_n} = 4n\).
(II). Dãy số \(\left( {{v_n}} \right)\) với \({v_n} = 2{n^2} + 1\).
(III). Dãy số \(\left( {{w_n}} \right)\) với \({w_n} = \frac{n}{3} - 7\).
(IV). Dãy số \(\left( {{t_n}} \right)\) với \({t_n} = \sqrt 5 - 5n\).
4.
3.
2.
1.
Cho cấp số nhân \(\left( {{u_n}} \right)\) có \({u_1} = - 3\) và \(q = \frac{2}{3}\). Mệnh đề nào sau đây đúng?
\({u_5} = - \frac{{27}}{{16}}.\)
\({u_5} = - \frac{{16}}{{27}}.\)
\({u_5} = \frac{{16}}{{27}}.\)
\({u_5} = \frac{{27}}{{16}}.\)
Ba cạnh của một tam giác vuông lập thành cấp số nhân. Tỉ số cạnh góc vuông nhỏ chia cho cạnh huyền là bao nhiêu?
\(\frac{{\sqrt 5 + 1}}{2}.\)
\(\frac{{\sqrt 5 - 1}}{2}.\)
\(\frac{{\sqrt 3 + 1}}{2}.\)
\(\frac{{\sqrt 3 - 1}}{2}.\)
\(\lim \frac{2}{{{n^2} + 1}}\) bằng
0.
2.
1.
\( + \infty .\)
Cho hai dãy \(\left( {{u_n}} \right)\) và \(\left( {{v_n}} \right)\) thỏa mãn \(\lim {u_n} = 3\) và \(\lim {v_n} = 1.\) Giá trị của \(\lim \frac{{{v_n}}}{{{u_n}}}\) bằng
3.
\(\frac{1}{3}.\)
\(2.\)
4.
\(\mathop {\lim }\limits_{x \to {1^ + }} \frac{{4x - 3}}{{x - 1}}\) bằng
\( + \infty .\)
2.
\[ - \infty .\]
\( - 2.\)
Trong bốn giới hạn sau đây, giới hạn nào bằng \( - \infty \)?
\(\mathop {\lim }\limits_{x \to + \infty } \frac{{ - 3x + 4}}{{x - 2}}.\)
\(\mathop {\lim }\limits_{x \to {2^ - }} \frac{{ - 3x + 4}}{{x - 2}}.\)
\(\mathop {\lim }\limits_{x \to {2^ + }} \frac{{ - 3x + 4}}{{x - 2}}.\)
\(\mathop {\lim }\limits_{x \to - \infty } \frac{{ - 3x + 4}}{{x - 2}}.\)
Cho hàm số \(y = f\left( x \right)\) xác định trên một khoảng \(K\) chứa \({x_0}\). Hàm số \(f\left( x \right)\) liên tục tại \({x_0}\) khi và chỉ khi
\(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = f\left( {{x_0}} \right).\)
\(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = \mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right).\)
\(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = f\left( {{x_0}} \right).\)
\(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right).\)
Cho hàm số \(f\left( x \right) = \frac{{{x^2} + 1}}{{{x^2} + 5x + 6}}\). Khi đó hàm số \(y = f\left( x \right)\) liên tục trên các khoảng nào sau đây?
\(\left( { - 3;2} \right).\)
\(\left( { - 2; + \infty } \right).\)
\(\left( { - \infty ;3} \right).\)
\(\left( {2;3} \right).\)
Trong không gian, cho 4 điểm không đồng phẳng. Có thể xác định được bao nhiêu mặt phẳng phân biệt từ các điểm đã cho?
4.
6.
2.
3.
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Gọi \(M,\,\,N\) lần lượt là trung điểm của \(AD\) và \(BC\). Giao tuyến của \(\left( {SMN} \right)\) và \(\left( {SAB} \right)\) là
\(SK\) (\(K\) là trung điểm của \(AB\)).
\(SO\) (\(O\) là tâm của hình bình hành \(ABCD\)).
\(d\) (\(d\) đi qua \(S\) và song song với \(AB\)).
\(d\) (\(d\) đi qua \(S\) và song song với \(BC\)).
Cho hai đường thẳng phân biệt \[a\] và \[b\] trong không gian. Có bao nhiêu vị trí tương đối giữa \[a\] và \[b\]?
3.
1.
2.
4.
Cho đường thẳng \(d\) song song với mặt phẳng \(\left( P \right)\). Mệnh đề nào sau đây đúng?
Đường thẳng \(d\) không có điểm chung với mặt phẳng \(\left( P \right)\).
Đường thẳng \(d\) có đúng một điểm chung với mặt phẳng \(\left( P \right)\).
Đường thẳng \(d\) có đúng hai điểm chung với mặt phẳng \(\left( P \right)\).
Đường thẳng \(d\) có vô số điểm chung với mặt phẳng \(\left( P \right)\).
Cho mặt phẳng \(\left( P \right)\) cắt hai mặt phẳng song song \(\left( Q \right)\) và \[\left( R \right)\] theo hai giao tuyến \(a\) và \(b.\) Mệnh đề nào sau đây đúng?
\(a\) và \(b\) có một điểm chung duy nhất.
\(a\) và \(b\) không có điểm chung.
\(a\) và \(b\) có vô số điểm chung.
\(a\) và \(b\) có hai điểm chung.
Cho hình hộp \(ABCD.A'B'C'D'\) như hình vẽ.

Mặt phẳng \(\left( {AA'B'} \right)\) song song với mặt phẳng nào sau đây?
\[\left( {AA'C'} \right).\]
\[\left( {AA'C'} \right).
\[\left( {DD'C'} \right).\]
\[\left( {ADD'} \right).\]
\[\left( {BB'A'} \right).\]
Hình lăng trụ ngũ giác có bao nhiêu cạnh?
15.
10.
5.
12.
Trong các mệnh đề sau mệnh đề nào sai?
Một đường thẳng luôn cắt hình chiếu của nó.
Một tam giác bất kỳ đề có thể xem là hình biểu diễn của một tam giác cân.
Một đường thẳng có thể song song với hình chiếu của nó
Hình chiếu song song của hai đường thẳng chéo nhau có thể song song với nhau.
Cho tứ diện \(ABCD.\) Gọi \(M\) là trung điểm của \(AB.\) Hình chiếu của \(M\) trên\(\left( {BCD} \right)\) theo phương \(AC\) là
Trung điểm của \(BD.\)
Trung điểm của \(BC.\)
Trọng tâm của \(\Delta BCD.\)
Điểm \(B.\)
(a) Chứng minh rằng \[\frac{{\sin 3x - \sin x}}{{2{{\cos }^2}x - 1}} = 2\sin x.\]
(b) Giải phương trình \[\cos x - \sin 2x = 0.\]
(a) Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} = 3;\,\,{u_2} = 1.\)Tính \({u_{11}}.\)
(b) Một du khách vào trường đua ngựa đặt cược, lần đầu đặt \(20\,\,000\) đồng, mỗi lần sau tiền đặt gấp đôi lần tiền đặt cọc trước. Người đó thua \(9\) lần liên tiếp và thắng ở lần thứ \(10.\) Hỏi du khách trên thắng hay thua bao nhiêu?
Tính các giới hạn sau:
(a) \(\lim \frac{{2020{n^2} - n}}{{2021 + {n^2}}};\)
(b) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {{x^2} + 2023} }}{{x + 1}}.\)
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành tâm \(O.\) Gọi \(M,\,\,N\) lần lượt là trung điểm của \(SA,\,\,CD.\)
(a) Chứng minh \(\left( {OMN} \right){\rm{//}}\left( {SBC} \right).\)
(b) Giả sử hai tam giác \(SAD\) và \(SAB\) là các tam giác cân tại \(A.\) Gọi \(AE\) và \(AF\) lần lượt là đường phân giác trong của hai tam giác \(SAD\) và \(SAB\). Chứng minh \(BD{\rm{//}}\left( {AEF} \right).\)