Bộ 10 đề thi cuối kì 1 Toán 11 Cánh diều có đáp án - Đề 1
37 câu hỏi
Cho góc hình học \(uOv\) có số đo \(50^\circ .\) Xác định số đo của góc lượng giác \(\left( {Ou,Ov} \right)\) trong hình dưới đây?
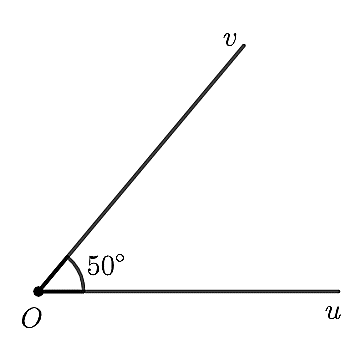
\(50^\circ + k360^\circ ,\,\,k \in \mathbb{Z}.\)
\(50^\circ + k180^\circ ,\,\,k \in \mathbb{Z}.\)
\( - 50^\circ + k360^\circ ,\,\,k \in \mathbb{Z}.\)
\( - 50^\circ + k180^\circ ,\,\,k \in \mathbb{Z}.\)
Đổi góc \(\alpha \) có số đo \(\frac{{3\pi }}{5}\) sang độ ta được số đo bằng độ là
\(150^\circ .\)
\(135^\circ .\)
\(144^\circ .\)
\(108^\circ .\)
Đẳng thức nào dưới đây là đúng?
\(\sin \left( {\alpha + \frac{\pi }{6}} \right) = \sin \alpha + \frac{1}{2}.\)
\(\sin \left( {\alpha + \frac{\pi }{6}} \right) = \frac{1}{2}\sin \alpha + \frac{{\sqrt 3 }}{2}\cos \alpha .\)
\(\sin \left( {\alpha + \frac{\pi }{6}} \right) = \frac{1}{2}\sin \alpha - \frac{{\sqrt 3 }}{2}\cos \alpha .\)
\(\sin \left( {\alpha + \frac{\pi }{6}} \right) = \frac{{\sqrt 3 }}{2}\sin \alpha + \frac{1}{2}\cos \alpha .\)
Cho \(\tan \left( {a + b} \right) = 3,\,\,\tan \left( {a - b} \right) = 2.\) Giá trị của \(\tan 2a\) là
\( - 1.\)
\(\frac{1}{7}.\)
\(1.\)
\( - \frac{1}{7}.\)
Tập xác định \(D\) của hàm số \(y = 2\tan x\) là
\(D = \mathbb{R}.\)
\(D = \mathbb{R}\backslash \left\{ 0 \right\}.\)
\(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}.\)
\(D = \mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}.\)
Cho các đồ thị hàm số sau:
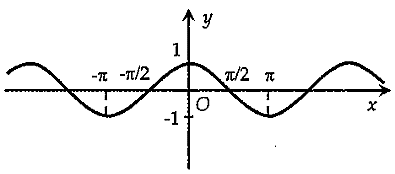 |
Hình 1
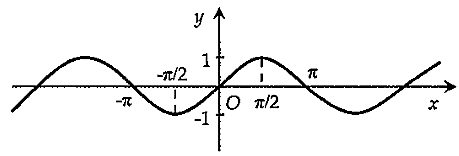
Hình 2
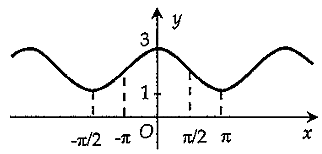
Hình 3
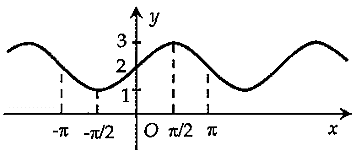
Hình 4
Hình nào là đồ thị của hàm số \(y = \sin x?\)
Hình 1.
Hình 2.
Hình 3.
Hình 4.
Phương trình \(\tan x = \tan \alpha \) có công thức nghiệm là
\[\left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\].
\[\left[ \begin{array}{l}x = \alpha + k\pi \\x = \pi - \alpha + k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\].
\[x = \pm \alpha + k2\pi \,\left( {k \in \mathbb{Z}} \right).\]
\[x = \alpha + k\pi \,\left( {k \in \mathbb{Z}} \right).\]
Nghiệm của phương trình \(\cos 2x = 1\) là
\(x = k\pi ,k \in \mathbb{Z}.\)
\(x = \frac{{k\pi }}{2},k \in \mathbb{Z}.\)
\(x = \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}.\)
\(x = - \frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}.\)
Có bao nhiêu giá trị nguyên của \(m\) để phương trình \(\sin x - 2m = 1\) có nghiệm?
3.
2.
1.
0.
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = 2n\). Năm số hạng đầu của dãy số \(\left( {{u_n}} \right)\) lần lượt là
\(2;\,\,4;\,\,6;\,\,8;\,\,10\).
\(0;\,\,2;\,\,4;\,\,6;\,\,8\).
\(1;\,\,2;\,\,3;\,\,4;\,\,5\).
\(0;\,\,1;\,\,2;\,\,3;\,\,4\).
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = {n^2} + 1.\) Dãy số \(\left( {{u_n}} \right)\) là dãy số
Không đổi.
Giảm.
Không tăng không giảm.
Tăng.
Trong các dãy số sau, dãy số nào là một cấp số cộng?
\({u_n} = - 3n + 2.\)
\({u_n} = {n^2} + 1.\)
\({u_n} = \frac{1}{{{n^2} + n}}.\)
\({u_n} = {2.3^n}.\)
Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} = 2\) và \(d = - 3\). Tính tổng 100 số hạng đầu của cấp số cộng đó?
\( - 29\,\,500.\)
\(10\,\,197.\)
\(15\,\,050.\)
\( - 14\,\,650.\)
Cho cấp số nhân \(\left( {{u_n}} \right)\) có công bội \(q.\) Mệnh đề nào sau đây đúng?
\[{u_n} = {u_1}.{q^{n - 1}},\,\forall n \ge 2.\]
\({u_n} = {u_1}{q^n},\,\,\forall n \ge 2.\)
\({u_n} = {u_1}.q,\,\,\forall n \ge 2.\)
\({u_n} = {u_1}.{q^{n + 1}},\,\,\forall n \ge 2.\)
Số hạng thứ 5 của một cấp số nhân \(\left( {{u_n}} \right)\) bằng \(162\) và số hạng thứ \(2\) bằng \(6.\)Số hạng thứ \(10\) của dãy số \(\left( {{u_n}} \right)\) là
\({u_{10}} = 39\,\,366.\)
\({u_{10}} = 118\,\,098.\)
\({u_{10}} = 972.\)
\({u_{10}} = 324.\)
Cho hàm số \(f\left( x \right)\) thỏa mãn \(\mathop {\lim }\limits_{x \to 1} f\left( x \right) = 2\). Giá trị của \[\mathop {\lim }\limits_{x \to 1} 4f\left( x \right)\] bằng
\(8\).
\(2\).
\(6\).
\(16\).
\(\mathop {\lim }\limits_{n \to + \infty } \frac{1}{{{n^2} + 1}}\) bằng
1.
\( + \infty .\)
\( - \infty .\)
0.
Cho các giới hạn: \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = 1;\,\,\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) = - 2\) thì \(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f\left( x \right) - g\left( x \right)} \right]\) bằng
\( - 2\).
\(2\).
\(3\).
\( - 3\).
Cho giới hạn \[\mathop {\lim }\limits_{x \to - 2} \left( {{x^2} - 2ax + 3 + {a^2}} \right) = 3\] thì \(a\) bằng bao nhiêu?
\(a = 2.\)
\(a = 0.\)
\(a = - 2.\)
\(a = 1.\)
Cho hàm số \(y = f\left( x \right)\) xác định trên khoảng K và \({x_0} \in K.\) Hàm số \(y = f\left( x \right)\)liên tục tại điểm \({x_0}\)khi
\(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right).\)
\(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right)\) không tồn tại.
\(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) \ne f\left( {{x_0}} \right).\)
\(f\left( {{x_0}} \right)\) không tồn tại.
Hàm số \[y = f\left( x \right)\] có đồ thị dưới đây gián đoạn tại điểm có hoành độ bằng bao nhiêu?
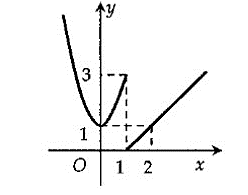
\[x = 1.\]
\[y = 1.\]
\[x = 2.\]
\[y = 3.\]
Cho hàm số \[f\left( x \right) = \left\{ \begin{array}{l}3x - 1\,\,{\rm{khi}}\,\,x \le - 2\\ax - 3\,\,{\rm{khi}}\,\,x > - 2\end{array} \right.\]. Với giá trị nào của \(a\) thì hàm số \(f\left( x \right)\) liên tục tại \(x = - 2\)?
\(a = 2.\)
\(a = 1.\)
\(a = 3.\)
\(a = - 2.\)
Trong các khẳng định sau, khẳng định nào đúng?
Qua 4 điểm phân biệt bất kì có duy nhất một mặt phẳng.
Qua 3 điểm phân biệt bất kì có duy nhất một mặt phẳng.
Qua 3 điểm không thẳng hàng có duy nhất một mặt phẳng.
Qua 2 điểm bất kì có duy nhất một mặt phẳng.
Cho tứ diện \(ABCD.\) Trên các cạnh \(AB\) và \(AC\) lấy hai điểm \(M\) và \(N\) sao cho \(AM = BM\) và \[AN = 2NC.\] Giao tuyến của hai mặt phẳng \(\left( {DMN} \right)\) và \(\left( {ACD} \right)\) là đường thẳng nào dưới đây?
\(MN.\)
\(DN.\)
\(DM.\)
\(AC.\)
Trong không gian, hai đường thẳng không có điểm chung thì
Cắt nhau.
Chéo nhau hoặc song song.
Chéo nhau.
Song song.
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(d\) là giao tuyến của hai mặt phẳng \(\left( {SAD} \right)\) và \(\left( {SBC} \right).\) Đường thẳng \(d\) song song với đường thẳng nào dưới đây?
Đường thẳng \(AB.\)
Đường thẳng \(AD.\)
Đường thẳng \[AC.\]
Đường thẳng \(SA.\)
Cho tứ diện \(ABCD.\) Gọi \(M,\,\,N\) lần lượt là trung điểm của \(AB,\,\,AC.\) Đường thẳng \(MN\) song song với mặt phẳng nào sau đây?
Mặt phẳng \(\left( {ABD} \right).\)
Mặt phẳng \(\left( {ACD} \right).\)
Mặt phẳng \[\left( {ABC} \right).\]
Mặt phẳng \(\left( {BCD} \right).\)
Hai hình bình hành \(ABCD\) và \(ABEF\) không cùng nằm trong một mặt phẳng. Gọi \(O\) và \(O'\) lần lượt là tâm hình bình hành \(ABCD\) và \(ABEF.\) \(OO'\) song song với
Mặt phẳng \(\left( {DCEF} \right).\)
Mặt phẳng \(\left( {ADF} \right).\)
Mặt phẳng \[\left( {BCE} \right).\]
Cả ba phương án A, B, C.
Cho hai đường thẳng song song \(a,\,\,b\) và mặt phẳng \(\left( P \right)\). Mệnh đề nào dưới đây đúng?
Nếu \(a{\rm{//}}\left( P \right)\) thì \(b{\rm{//}}\left( P \right).\)
Nếu \(a\) cắt \(\left( P \right)\) thì \(b\) cắt \(\left( P \right).\)
Nếu \(a\) nằm trên \(\left( P \right)\) thì \(b{\rm{//}}\left( P \right).\)
Nếu \(a\) nằm trên \(\left( P \right)\) thì \(b\) nằm trên \(\left( P \right).\)
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành tâm \(O.\) Gọi \(M,\,\,N,\,\,P\) theo thứ tự lần lượt là trung điểm của \(SA,\,\,SB,\,\,SD.\) Khẳng định nào sau đây sai?
\(\left( {MNP} \right){\rm{//}}\left( {ABCD} \right).\)
\(\left( {MNP} \right){\rm{//}}\left( {SCD} \right).\)
\(MN{\rm{//}}\left( {ABCD} \right).\)
\(MP{\rm{//}}\left( {ABCD} \right).\)
Cho mặt phẳng \(\left( R \right)\) cắt hai mặt phẳng song song \(\left( P \right)\) và \[\left( Q \right)\] theo hai giao tuyến \(a\) và \(b.\) Mệnh đề nào sau đây đúng?
\(a\) và \(b\) có một điểm chung duy nhất.
\(a\) và \(b\) song song.
\(a\) và \(b\) trùng nhau.
\(a\) và \(b\) song song hoặc trùng nhau.
Mệnh đề sai trong các mệnh đề sau:
Hình lăng trụ có đáy là tam giác được gọi là lăng trụ tam giác.
Hình lăng trụ có đáy là tứ giác được gọi là lăng trụ hộp.
Hình lăng trụ có đáy là tứ giác được gọi là lăng trụ tứ giác.
Hình lăng trụ tứ giác có hai đáy là hình bình hành được gọi là hình hộp.
Cho hình hộp \(ABCD.A'B'C'D'\)(hình vẽ dưới).
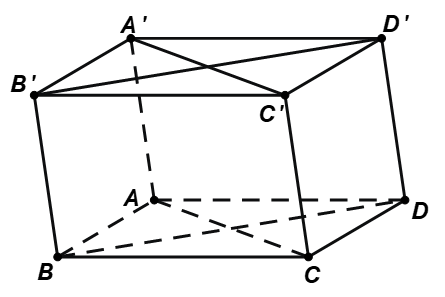
Mệnh đề nào sau đây sai?
\(\left( {BDD'B'} \right)\;{\rm{//}}\;\left( {ACC'A'} \right)\).
\(\left( {AA'D'D} \right)\;{\rm{//}}\;\left( {BCC'B'} \right)\).
\(\left( {ABCD} \right)\;{\rm{//}}\;\left( {A'B'C'D'} \right)\).
\(\left( {ABB'A'} \right)\;{\rm{//}}\;\left( {CDD'C'} \right)\).
Hình chiếu của hình chữ nhật không thể là hình nào trong các hình sau?
Hình thang.
Hình bình hành.
Hình chữ nhật.
Hình thoi.
Cho hình lăng trụ tam giác \(ABC.A'B'C'.\)

Hình chiếu của tam giác \(ACB\) trên mặt phẳng \(\left( {A'B'C'} \right)\) theo phương \(CC'\) là
Tam giác \(A'C'B'.\)
Đoạn thẳng \(A'B'.\)
Tam giác \(A'B'C'.\)
Đoạn thẳng \(A'C'.\)
Tính các giới hạn sau:
(a) \[\mathop {\lim }\limits_{n \to + \infty } \left( {\sqrt {{n^2} + n} - \sqrt {{n^2} + 1} } \right).\]
(b) \(\mathop {\lim }\limits_{x \to \frac{\pi }{6}} \frac{{2\tan x + 1}}{{\sin x + 1}}\).
Gia đình ông An cần khoan một cái giếng. Biết rằng giá của mét khoan đầu tiên là 200 000 đồng và kể từ mét khoan thứ hai, giá của mỗi mét khoan sau sẽ tăng thêm \(6\% \) so với giá của mét khoan trước đó. Hỏi nếu ông An khoan cái giếng sâu 35 m thì hết bao nhiêu tiền (làm tròn đến hàng nghìn).