Bộ 5 đề thi giữa kì 1 Toán 11 Cánh diều cấu trúc mới có đáp án - Đề 4
22 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, học sinh chỉ chọn một phương án
Cho \[0 < x < \frac{\pi }{2}\]. Mệnh đề nào sau đây là đúng?
\[\tan x > 0,\cot x > 0.\]
\[\tan x > 0,\cot x < 0.\]
\[\tan x < 0,\cot x < 0.\]
\[\tan x < 0,\cot x > 0.\]
Mệnh đề nào sau đây là sai?
Hàm số \[y = \tan x\] tuần hoàn với chu kì \[\pi \].
Hàm số \[y = \sin x\] tuần hoàn với chu kì \[2\pi \].
Hàm số \[y = \cos x\] tuần hoàn với chu kì \[2\pi \].
Hàm số \[y = \cot x\] tuần hoàn với chu kì \[2\pi \].
Rút gọn biểu thức \[M = \cos 2x.\cos x + \sin 2x.\sin x\] ta được kết quả là
\[M = \cos x.\]
\[M = \cos 3x.\]
\[M = \sin x.\]
\[M = \sin 3x.\]
Nghiệm của phương trình \[\sqrt 3 \cot \left( {2x + \frac{\pi }{6}} \right) = 1\] là:
\[x = \frac{\pi }{{12}} + \frac{{k\pi }}{2},{\rm{ }}\left( {k \in \mathbb{Z}} \right).\]
\[x = \pm \frac{\pi }{{12}} + \frac{{k\pi }}{2},{\rm{ }}\left( {k \in \mathbb{Z}} \right).\]
\[x = \frac{\pi }{6} + k\pi ,{\rm{ }}\left( {k \in \mathbb{Z}} \right).\]
\[x = \frac{\pi }{3} + k\pi ,{\rm{ }}\left( {k \in \mathbb{Z}} \right).\]
Cho dãy số có các số hạng đầu là: \[\frac{1}{3};\frac{1}{{{3^2}}};\frac{1}{{{3^3}}};\frac{1}{{{3^4}}};\frac{1}{{{3^5}}};....\] Số hạng tổng quát của dãy số này là
\[{u_n} = \frac{1}{3}.\frac{1}{{{3^{n + 1}}}}.\]
\[{u_n} = \frac{1}{{{3^{n + 1}}}}.\]
\[{u_n} = \frac{1}{{{3^n}}}.\]
\[{u_n} = \frac{1}{{{3^{n - 1}}}}.\]
Trong các dãy số sau, dãy nào không phải cấp số cộng?
\[\frac{1}{2};\frac{3}{2};\frac{5}{2};\frac{7}{2};\frac{9}{2}.\]
\[1;1;1;1;1.\]
\[ - 8; - 6; - 4; - 2;0.\]
\[3;1; - 1; - 2; - 4.\]
Cho cấp số nhân \[\left( {{u_n}} \right)\], biết \[{u_1} = 2,{u_2} = 8\]. Công bội \[q\] của cấp số nhân đã cho là
\[16.\]
\[4.\]
\[10.\]
\[6.\]
Cho dãy số \[\left( {{u_n}} \right)\] biết \[{u_n} = \frac{{10}}{{{3^n}}}\]. Mệnh đề nào sau đây đúng?
Dãy số tăng.
Dãy số giảm.
Dãy số không tăng, không giảm.
Dãy số vừa tăng vừa giảm.
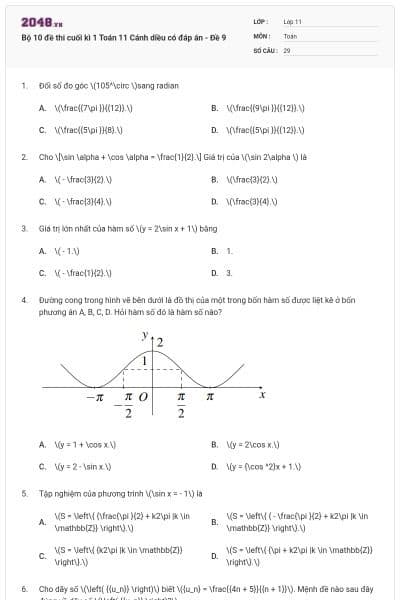
Trong các hình sau
Hình nào có thể là hình biểu diễn một tứ diện?
\[\left( I \right).\]
\[\left( I \right),\left( {II} \right).\]
\[\left( I \right),\left( {II} \right),\left( {IV} \right).\]
\[\left( I \right),\left( {II} \right),\left( {III} \right),\left( {IV} \right).\]
Cho hình tứ diện \[ABCD\]. Giao tuyến của hai mặt phẳng \[\left( {ABC} \right)\] và \[\left( {CDA} \right)\] là đường thẳng.
\[AC.\]
\[CD.\]
\[AB.\]
\[BD.\]
Cho tứ diện \[ABCD\]. Gọi \[M,N\] lần lượt là trung điểm của \[BA,BC\]. Trong các đường thẳng sau, đường nào song song với \[MN\]?
\[AC.\]
\[CD.\]
\[AB.\]
\[BD.\]
Cho tứ diện \[ABCD\]. Gọi \[M,N\] lần lượt là trung điểm của \[AC,CD\]. Giao tuyến của hai mặt phẳng \[\left( {MBD} \right)\] và \[\left( {ABN} \right)\] là
Đường thẳng \[MN.\]
Đường thẳng \[AM.\]
Đường thẳng \[BG\] (\[G\] là trọng tâm tam giác \[ACD\]).
Đường thẳng \[AH\] (\[H\] là trực tâm tam giác \[ACD\]).
Phần II. Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu hỏi, học sinh chọn Đúng hoặc Sai.
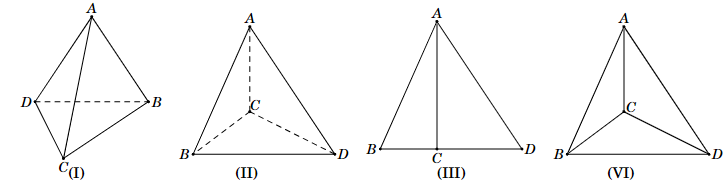
Cho hàm số \[y = \cot x\]. Xét tính đúng – sai của các phát biểu sau:
a) \[y = \cot x\] là hàm số lẻ, đồ thị đối xứng qua trục tung.
b) Đồ thị hàm số \[y = \cot x\] có dạng:
c) Đồ thị hàm số \[y = \cot x\] cắt trục hoành tại 3 điểm có hoành độ trong khoảng \[\left( {0;2\pi } \right).\]
d) Tổng các nghiệm của phương trình \[\cot x = \sqrt 3 \] trong khoảng \[\left( {0;2\pi } \right)\] là \[\frac{{3\pi }}{2}\].
Một vật dao động xung quanh vị trí cân bằng theo phương trình \[x = 1,5\cos \left( {\frac{{\pi t}}{4}} \right);\] trong đó \[t\] là thời gian được tính bằng giây và quãng đường \[h = \left| x \right|\] được tính bằng mét là khoảng cách theo phương ngang của chất điểm đối với vị trí cân bằng. Xét tính đúng sai của các khẳng định sau:
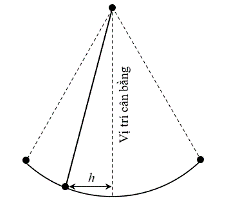
a) Vật ở xa vị trí cân bằng nhất nghĩa là \[h = 1,5{\rm{ m}}\].
b) Trong 10 giây đầu tiên, có hai thời điểm vật ở xa vị trí cân bằng nhất.
c) Khi vật ở vị trí cân bằng thì \[\cos \left( {\frac{{\pi t}}{4}} \right) = 0\].
d) Trong khoảng từ \[0\] đến \[20\] giây thì vật qua vị trí cân bằng 4 lần.
Một sinh viên sau khi ra trường và xin vào làm cho một trung tâm với mức lương khởi điểm là \[100\] triệu đồng một năm. Cứ sau mỗi năm, trung tâm trả thêm cho sinh viên \[20\] triệu đồng. Gọi \[{u_n}\] (triệu đồng) là số tiền lương mà sinh viên đó nhận được ở năm thứ \[n\]. Xét tính đúng sai của các khẳng định sau:
a) Số tiền lương sinh viên nhận được ở năm thứ hai là \[120\] triệu đồng.
b) Số tiền lương sinh viên nhận được ở năm thứ 10 là \[300\] triệu đồng.
c) Tiền lương sau mỗi năm của sinh viên đó là cấp số cộng có \[{u_1} = 120\] và công sai \[d = 20\].
d) Giả sử, mỗi năm bạn sinh viên chi tiêu tiết kiệm \[70\] triệu đồng. Vậy sau ít nhất \[12\] năm thì sinh viên đó mua được căn chung cư \[2\] tỉ đồng.
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình chữ nhật. Gọi \[I,J\] lần lượt là trung điểm của các cạnh \[AD,BC\] và \[G\] là trọng tâm của tam giác \[SAB\]. Khi đó:
a) Giao tuyến của hai mặt phẳng \[\left( {SAB} \right)\] và \[\left( {SCD} \right)\] là đường thẳng qua \[S\] và song song với \[AB\].
b) Giao tuyến của hai mặt phẳng \[\left( {SAC} \right)\] và \[\left( {SBD} \right)\] là đường thẳng qua \[S\] và song song với \[AC\].
c) Giao tuyến của hai mặt phẳng \[\left( {SAB} \right)\] và \[\left( {IGJ} \right)\] là đường thẳng qua \[G\] và song song với \[CD\].
d) Lấy \[M\] trên \[SD\] sao cho \[SM = \frac{2}{3}SD\], \[N\] trên \[SA\] sao cho \[NA = \frac{1}{3}SA.\] Giao tuyến của hai mặt phẳng \[\left( {GMN} \right)\] và \[\left( {GBC} \right)\] là đường thẳng qua \[G\] và song song với \[AD.\]
Phần III. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 1 đến câu 6.
Tập hợp các giá trị của tham số \[m\] để phương trình \[\sin 2x + 2 = m\] có nghiệm là \[\left[ {a;b} \right]\]. Khi đó tính giá trị \[T = a + 2b\].
Giả sử một vật dao động điều hòa xung quanh vị trí cân bằng theo phương trình \[x = 2\cos \left( {5t - \frac{\pi }{6}} \right)\]. Ở đây, thời gian \[t\] tính bằng giây và quãng đường \[x\] tính bằng centimét, vật đi qua vị trí cân bằng bao nhiêu lần trong 3 giây đầu?
Một loại vi khuẩn sau mỗi phút số lượng được tăng gấp đôi biết rằng sau 5 phút người ta đếm được \[64000\] con. Hỏi sau bao nhiêu phút thì có được \[2048000\] con?
Cho dãy số \[\left( {{u_n}} \right)\] thỏa mãn \[\left\{ \begin{array}{l}5{u_1} + \sqrt {5{u_1} - {u_2}} = {u_2} + 6\\{u_{n + 1}} = 3{u_n},{\rm{ }}\forall n \in {\mathbb{N}^ * }\end{array} \right.\]. Giá trị nhỏ nhất của \[n\] để \[{u_n} \ge {2.3^{2018}}\] bằng bao nhiêu?
Cho hình chóp tứ giác đều \[S.ABCD\] có cạnh đáy bằng 1. Các điểm \[M,N,P\] lần lượt là trung điểm của \[SA,SB,SC\]. Mặt phẳng \[\left( {MNP} \right)\] cắt hình chóp theo một thiết diện có diện tích bằng bao nhiêu?
Cho tứ diện \[ABCD\]. Các điểm \[P,Q\] lần lượt là trung điểm của \[AB\] và \[CD\]; điểm \[R\] nằm trên cạnh \[BC\] sao cho \[BR = 2RC\]. Gọi \[S\] là giao điểm của mặt phẳng \[\left( {PQR} \right)\] và cạnh \[AD\]. Tính tỉ số \[\frac{{SA}}{{SD}}\].