Bộ 5 đề thi giữa kì 1 Toán 11 Cánh diều cấu trúc mới có đáp án - Đề 3
22 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, học sinh chỉ chọn một phương án
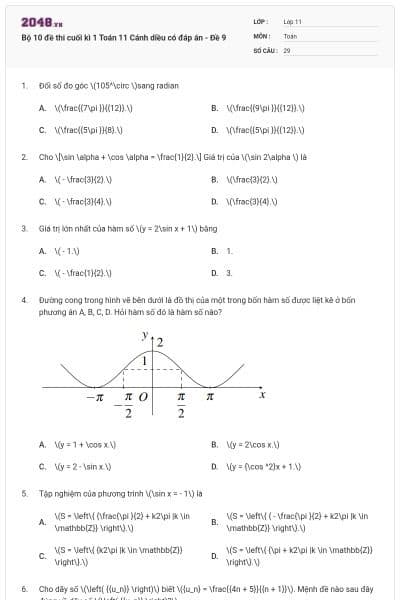
Đường cong dưới đây là đồ thị hàm số của hàm số nào trong các đáp án A, B, C, D?
\[y = \sin x.\]
\[y = \cos x.\]
\[y = \tan x.\]
\[y = \cot x.\]
Cho \[\sin x = \frac{4}{5}\] với \[\frac{\pi }{2} < x < \pi \]. Giá trị của \[\cos x\] bằng
\[\frac{1}{5}.\]
\[\frac{3}{5}.\]
\[ - \frac{3}{5}.\]
\[\frac{4}{5}.\]
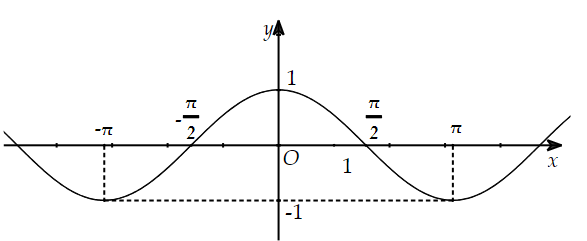
Xác định số đo của góc lượng giác \[\left( {Ou,Ov} \right)\] được biểu diễn trong hình bên dưới đây.
![Xác định số đo của góc lượng giác \[\left( {Ou,Ov} \right)\] được biểu diễn trong hình bên dưới đây. A. \[ - 300^\circ .\] B. \[510^\circ .\] C. \[60^\circ .\] D. \[ - 420^\circ .\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/17-1760799467.png)
\[ - 300^\circ .\]
\[510^\circ .\]
\[60^\circ .\]
\[ - 420^\circ .\]
Tập xác định của hàm số \[y = \frac{{\sin x}}{{1 - \cos x}}\] là
\[D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}.\]
\[D = \mathbb{R}\backslash \left\{ {k\pi |k \in \mathbb{Z}} \right\}.\]
\[D = \mathbb{R}\backslash \left\{ {k2\pi |k \in \mathbb{Z}} \right\}.\]
\[D = \mathbb{R}\backslash \left\{ {\frac{{k\pi }}{2}|k \in \mathbb{Z}} \right\}.\]
Nghiệm của phương trình \[2\sin x - \sqrt 3 = 0\] là
\[\left[ \begin{array}{l}x = \frac{\pi }{3} + k2\pi \\x = \frac{{2\pi }}{3} + k2\pi \end{array} \right.,{\rm{ }}k \in \mathbb{Z}.\]
\[\left[ \begin{array}{l}x = \frac{\pi }{6} + k2\pi \\x = \frac{{5\pi }}{6} + k2\pi \end{array} \right.,{\rm{ }}k \in \mathbb{Z}.\]
\[x = \pm \frac{\pi }{6} + k2\pi ,{\rm{ }}k \in \mathbb{Z}.\]
\[x = \pm \frac{\pi }{2} + k2\pi ,{\rm{ }}k \in \mathbb{Z}.\]
Trong các dãy số sau, dãy số nào là một cấp số cộng?
\[1; - 2; - 4; - 6; - 8.\]
\[1; - 3; - 6; - 9; - 12.\]
\[1; - 3; - 7; - 11; - 15.\]
\[1; - 3; - 5; - 7; - 9.\]
Cho cấp số nhân \[\left( {{u_n}} \right)\] có \[{u_1} = - 2\] và công bội \[q = 3\]. Giá trị của \[{u_2}\] bằng
\[6.\]
\[ - 6.\]
\[1.\]
\[ - 18.\]
Cho cấp số cộng \[\left( {{u_n}} \right)\] có \[{u_1} = 1\] và công sai \[d = 2\]. Tổng 10 số hạng đầu tiên của dãy là
\[{S_{10}} = 110.\]
\[{S_{10}} = 100.\]
\[{S_{10}} = 21.\]
\[{S_{10}} = 19.\]
Hình chóp tứ giác có tất cả bao nhiêu mặt là tam giác?
\[6.\]
\[3.\]
\[4.\]
\[5.\]
Cho tứ diện \[ABCD\] như hình bên. Mệnh đề nào sau đây là đúng?
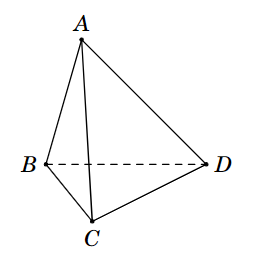
\[AB\] và \[CD\] cắt nhau.
\[BD\] và \[AC\] cắt nhau.
\[BD\] và \[AC\] chéo nhau.
\[CB\] và \[AD\] song song.
Cho hình chóp tứ giác \[S.ABCD\] có đáy \[ABCD\] là hình bình hành. Gọi \[I,J\] lần lượt là trung điểm của \[SA\] và \[SB\]. Khẳng định nào sau đây là sai?
\[\left( {SAB} \right) \cap \left( {IBC} \right) = IB.\]
\[CDIJ\]là hình thang.
\[\left( {SBD} \right) \cap \left( {JCD} \right) = JD.\]
\[\left( {IAC} \right) \cap \left( {IBD} \right) = AO\] (\[O\] là tâm \[ABCD\]).
Cho hình chóp \[S.ABCD\] có đáy là hình bình hành. Gọi \[M,N\] lần lượt là trung điểm của \[AD\] và \[BC\]. Giao tuyến của hai mặt phẳng \[\left( {SMN} \right)\] và \[\left( {SAC} \right)\] là
\[SK\] với \[K\] là trung điểm của \[AB.\]
\[SO\] với \[O\] là tâm của hình bình hành \[ABCD.\]
\[SF\] với \[F\] là trung điểm của \[CD.\]
\[SD.\]
Phần II. Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu hỏi, học sinh chọn Đúng hoặc Sai.
Cho phương trình lượng giác \[\sin \left( {3x + \frac{\pi }{3}} \right) = - \frac{{\sqrt 3 }}{2}\]. Khi đó:
a) Phương trình có nghiệm \[\left[ \begin{array}{l}x = - \frac{\pi }{9} + k\frac{{2\pi }}{3}\\x = \frac{\pi }{3} + k\frac{{2\pi }}{3}\end{array} \right.,{\rm{ }}k \in \mathbb{Z}.\]
b) Phương trình có nghiệm âm lớn nhất là \[ - \frac{{2\pi }}{9}.\]
c) Trên khoảng \[\left( {0;\frac{\pi }{2}} \right)\] phương trình đã cho có 3 nghiệm.
d) Tổng các nghiệm của phương trình trong khoảng \[\left( {0;\frac{\pi }{2}} \right)\] là \[\frac{{7\pi }}{9}.\]
Chiều cao so với mực nước biển trung bình tại các thời điểm \[t\] (giây) của mỗi cơn sóng được cho bởi hàm số \[h\left( t \right) = 75\sin \left( {\frac{{\pi t}}{8}} \right)\], trong đó \[h\left( t \right)\] được tính bằng centimét. (Tất cả các kết quả được làm tròn đến hàng phần mười).
a) Chiều cao của sóng tại thời điểm 5 giây bằng \[69,3{\rm{ }}\left( {cm} \right)\].
b) Chiều cao của sóng tại thời điểm 20 giây bằng \[{\rm{75 }}\left( {cm} \right)\].
c) Trong 30 giây đầu tiên (kể từ mốc \[t = 0\] giây), thời điểm để sóng đạt chiều cao lớn nhất là 6 giây.
d) Trong 30 giây đầu tiên (kể từ mốc \[t = 0\] giây), thời điểm để sóng đạt chiều cao lớn nhất là 18 giây.
Cho cấp số cộng \[\left( {{u_n}} \right)\] có công sai \[d < 0\] thỏa mãn \[\left\{ \begin{array}{l}{u_1} + {u_7} = 26\\u_2^2 + u_6^2 = 466\end{array} \right.\]. Khi đó:
a) Số hạng \[{u_1} = 25.\]
b) Công sai \[d = - 3.\]
c) Số hạng \[{u_{10}} = - 11.\]
d) Số hạng \[{u_{2024}} = - 8067.\]
Cho hình chóp \[S.ABCD\], biết \[AB\] cắt \[CD\] tại \[E\], \[AC\] cắt \[BD\] tại \[F\] trong mặt phẳng đáy. Xét tính đúng sai của các khẳng định sau:
a) Đường thẳng \[FE\] nằm trong mặt phẳng \[\left( {ABCD} \right).\]
b) \[AB\] là giao tuyến của hai mặt phẳng \[\left( {SAB} \right)\] và \[\left( {ABCD} \right).\]
c) \[SF\] là giao điểm của hai mặt phẳng \[\left( {SAB} \right)\] và \[\left( {SCD} \right)\], \[SE\] là giao tuyến của hai mặt phẳng \[\left( {SAC} \right)\] và \[\left( {SBD} \right).\]
d) Gọi \[G = FE \cap AD\]. Khi đó, \[SG\] là giao tuyến của mặt phẳng \[\left( {SFE} \right)\] và mặt phẳng \[\left( {SAD} \right)\].
Phần III. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 1 đến câu 6.
Có bao nhiêu số nguyên \[m\] để phương trình \[3\cos \left( {x + \frac{\pi }{6}} \right) - m + 5 = 0\] có nghiệm?
Cho biết bốn số \[5;x;15;y\] lập thành một cấp số cộng. Tính giá trị của biểu thức \[T = 3x + 2y\].
Cho hình chóp \[S.ABCD\] có đáy là hình bình hành. \[M\]là trung điểm của \[SC\]. Gọi \[I\] là giao điểm của đường thẳng \[AM\] với mặt phẳng \[\left( {SBD} \right)\]. Tính tỉ số \[\frac{{IA}}{{IM}}\].
Một cây cầu có dạng cung \[OA\] là một phần của đồ thị hàm số \[y = 4,8\sin \frac{x}{5}\] và được mô tả trong hệ trục tọa độ với đơn vị trục là mét như hình bên.
![Một cây cầu có dạng cung \[OA\] là một phần của đ (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/23-1760800085.png)
Giả sử chiều rộng của con sông là đoạn thẳng \[OA\]. Tính chiều rộng của con sông đó. (Làm tròn kết quả đến hàng phần mười).
Ban đầu có bốn triệu con vi khuẩn trong phòng thí nghiệm, người ta cho vào đám vi khuẩn đó một chất kháng khuẩn thì số lượng vi khuẩn giảm đi một nửa so với trước đó sau mỗi 6 giờ. Vậy sau 24 giờ số lượng vi khuẩn còn lại là bao nhiêu? (đơn vị: nghìn con).
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình bình hành. Gọi \[G\] là trọng tâm tam giác \[ABC\] và \[M\] là trung điểm \[SC\]. Gọi \[K\] là giao điểm của \[SD\] và mặt phẳng \[\left( {AGM} \right)\]. Tính tỉ số \[\frac{{KS}}{{KD}}\].