Bộ 5 đề thi giữa kì 1 Toán 11 Cánh diều cấu trúc mới có đáp án - Đề 1
22 câu hỏi
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, học sinh chỉ chọn một phương án
Góc có số đo \[108^\circ \] đổi sang radian là
\[\frac{{3\pi }}{2}.\]
\[\frac{{5\pi }}{2}.\]
\[\frac{{5\pi }}{3}.\]
\[\frac{{3\pi }}{5}.\]
Chọn khẳng định đúng trong các khẳng định sau:
\[\tan \left( {\pi - \alpha } \right) = \tan \alpha .\]
\[\cot \left( {\pi - \alpha } \right) = \cot \alpha .\]
\[\cos \left( {\pi - \alpha } \right) = - \cos \alpha .\]
\[\sin \left( {\pi - \alpha } \right) = - \sin \alpha .\]
Tập xác định của hàm số \[y = \frac{{2025}}{{\sin x}}\] là
\[D = \mathbb{R}.\]
\[D = \mathbb{R}\backslash \left\{ 0 \right\}.\]
\[D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,{\rm{ }}k \in \mathbb{Z}} \right\}.\]
\[D = \mathbb{R}\backslash \left\{ {k\pi ,{\rm{ }}k \in \mathbb{Z}} \right\}.\]
Nếu \[\sin x + \cos x = \frac{1}{2}\] thì \[\sin 2x\] bằng
\[\frac{3}{4}.\]
\[\frac{3}{8}.\]
\[\frac{{\sqrt 2 }}{2}.\]
\[ - \frac{3}{4}.\]
Nghiệm của phương trình \[2\sin x + 1 = 0\] là
\[\left[ \begin{array}{l}x = 30^\circ + k360^\circ \\x = 210^\circ + k360^\circ \end{array} \right.,{\rm{ }}\left( {k \in \mathbb{Z}} \right).\]
\[\left[ \begin{array}{l}x = - 30^\circ + k360^\circ \\x = 210^\circ + k360^\circ \end{array} \right.,{\rm{ }}\left( {k \in \mathbb{Z}} \right).\]
\[\left[ \begin{array}{l}x = 180^\circ + k360^\circ \\x = 45^\circ + k360^\circ \end{array} \right.,{\rm{ }}\left( {k \in \mathbb{Z}} \right).\]
\[\left[ \begin{array}{l}x = - 30^\circ + k360^\circ \\x = 150^\circ + k360^\circ \end{array} \right.,{\rm{ }}\left( {k \in \mathbb{Z}} \right).\]
Dãy số \[\left( {{u_n}} \right)\] là dãy số tăng khi và chỉ khi
\[{u_n} < {u_{n + 1}},{\rm{ }}\forall n \in {\mathbb{N}^ * }.\]
\[{u_n} > {u_{n + 1}},{\rm{ }}\forall n \in {\mathbb{N}^ * }.\]
\[{u_n} \ge {u_{n + 1}},{\rm{ }}\forall n \in {\mathbb{N}^ * }.\]
\[{u_n} \le {u_{n + 1}},{\rm{ }}\forall n \in {\mathbb{N}^ * }.\]
Trong các dãy số sau, dãy nào là một cấp số cộng?
\[1; - 3; - 6; - 9; - 12.\]
\[1; - 3; - 7; - 11; - 15.\]
\[1; - 3; - 5; - 7; - 9.\]
\[1; - 2; - 4; - 6; - 8.\]
Cho cấp số cộng \[\left( {{u_n}} \right)\] có \[{u_1} = 1\] và công sai \[d = 3\]. Tổng 4 số hạng đầu của \[\left( {{u_n}} \right)\] là:
\[{S_4} = 9.\]
\[{S_4} = 12.\]
\[{S_4} = 22.\]
\[{S_4} = 14.\]
Phát biểu nào dưới đây là sai?
\[\lim {q^n} = 0{\rm{ }}\left( {\left| q \right| > 1} \right).\]
\[\lim C = C\](\[C\]là hằng số).
\[\lim \frac{1}{{{n^k}}} = 0\] (\(k\) nguyên dương).
\[\lim {n^k} = 0{\rm{ }}\left( {k < 0,k \in \mathbb{Z}} \right).\]
Giới hạn của dãy số \(\left( {{u_n}} \right)\) với \[{u_n} = \frac{{\sqrt {9{n^2} - n + 1} }}{{4n}}\] là
\[\frac{3}{4}.\]
\[ - \frac{3}{4}.\]
\[\frac{9}{4}.\]
\[ - \frac{9}{4}.\]
Cho hình chóp \[S.ABCD\]. Giao tuyến của hai mặt phẳng \[\left( {SAB} \right)\] và \[\left( {SBC} \right)\] là
\[SA.\]
\[SB.\]
\[SC.\]
\[AC.\]
Cho tứ diện \[ABCD\]. Gọi \[M,N\] lần lượt là trung điểm \[AD\] và \[AC\]. Gọi \[G\] là trọng tâm tam giác \[BCD\]. Giao tuyến của hai mặt phẳng \[\left( {GMN} \right)\] và \[\left( {BCD} \right)\] là đường thẳng:
qua \[M\] và song song với \[AB.\]
qua \[N\] và song song với \[BD.\]
qua \[G\] và song song với \[CD.\]
qua \[G\] và song song với \[BC.\]
Phần II. Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu hỏi, học sinh chọn Đúng hoặc Sai.
Trong hình vẽ bên, ta xem hình ảnh đường tròn trên một bánh lái tàu thủy tương ứng với một đường tròn lượng giác.
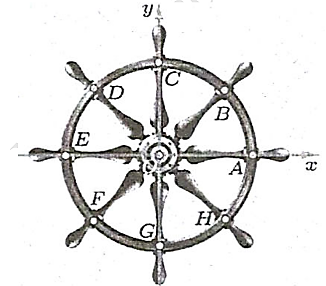
a) Công thức tổng quát biểu diễn góc lượng giác \[\left( {OA,OB} \right)\] theo đơn vị radian là
\[\left( {OA,OB} \right) = \frac{\pi }{4} + k2\pi {\rm{ }}\left( {k \in \mathbb{Z}} \right).\]
b) Công thức tổng quát biểu diễn góc lượng giác tương ứng với bốn điểm biểu diễn là \[A,C,E,G\] theo đơn vị radian là \[\frac{{k\pi }}{3},{\rm{ }}\left( {k \in \mathbb{Z}} \right).\]
c) Công thức tổng quát biểu diễn góc lượng giác tương ứng với hai điểm biểu diễn là \[A,E\] theo đơn vị đo độ là \[k180^\circ {\rm{ }}\left( {k \in \mathbb{Z}} \right).\]
d) Công thức tổng quát biểu diễn góc lượng giác \[\left( {OA,OC} \right) + \left( {OC,OH} \right)\] theo đơn vị radian là \[\frac{\pi }{4} + k2\pi ,{\rm{ }}\left( {k \in \mathbb{Z}} \right).\]
Số giờ có ánh sáng mặt trời của một thành phố A trong ngày thứ \[t\] (ở đây \[t\] là số ngày tính từ ngày 1 tháng giêng) của một năm không nhuận được mô hình hóa bởi hàm số
\[L\left( t \right) = 12 + 2,83\sin \left[ {\frac{{2\pi }}{{365}}\left( {t - 80} \right)} \right],{\rm{ }}\left( {t \in \mathbb{Z},{\rm{ }}0 < t \le 365} \right).\]
a) Tập giá trị của hàm số \[L\left( t \right)\] là \[\left[ {9,17;14,83} \right].\]
b) Ngày thành phố A có ít ánh sáng mặt trời nhất tương ứng với \[\sin \left[ {\frac{{2\pi }}{{365}}\left( {t - 80} \right)} \right] = - 1.\]
c) Ngày thành phố A có ít ánh sáng mặt trời nhất là vào ngày thứ 352 của năm.
d) Ngày thành phố A có nhiều ánh sáng mặt trời nhất là ngày thứ 171, tức là khoảng ngày 20 tháng 6.
Cho cấp số nhân \[\left( {{u_n}} \right)\] có công bội nguyên và các số hạng thỏa mãn:
\[\left\{ \begin{array}{l}{u_4} - {u_2} = 54\\{u_5} - {u_3} = 108\end{array} \right.\]
a) Số hạng đầu là \[{u_1} = 9.\]
b) Công bội của cấp số nhân là \[q = 3.\]
c) Tổng của 9 số hạng đầu tiên bằng \[4599.\]
d) Số \[576\] là số hạng thứ 6 của cấp số nhân.
Cho tứ diện \[ABCD\]. Gọi \[I,J\] lần lượt là trung điểm của \[AD,BC\], \[M\] là một điểm trên cạnh \[AB\], \[N\] là một điểm trên cạnh \[AC\]. Khi đó:
a) \[IJ\] là giao tuyến của hai mặt phẳng \[\left( {IBC} \right),\left( {JAD} \right).\]
b) \[ND\] là giao tuyến của hai mặt phẳng \[\left( {NMD} \right),\left( {ADC} \right).\]
c) \[BI\] là giao tuyến của hai mặt phẳng \[\left( {BIC} \right),\left( {ABD} \right).\]
d) Giao tuyến của hai mặt phẳng \[\left( {IBC} \right),\left( {DMN} \right)\] song song với đường thẳng \[IJ.\]
Phần III. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 1 đến câu 6.
Tính giá trị lớn nhất của hàm số \[y = 2{\cos ^2}x - \sqrt 3 \sin 2x + 2018\].
Hằng ngày mực nước của con kênh lên xuống theo thủy triều. Độ sâu \[h\] (mét) của mực nước trong kênh được tính tại thời điểm \[t\] (giờ) trong một ngày bởi công thức \[h = 3\cos \left( {\frac{{\pi t}}{8} + \frac{\pi }{4}} \right) + 12\]. Mực nước của kênh cao nhất khi \[t\] bằng bao nhiêu?
Cho cấp số nhân \[\left( {{u_n}} \right)\] có \[{u_1} = 3\] và \[15{u_1} - 4{u_2} + {u_3}\] đạt giá trị nhỏ nhất. Tìm số hạng thứ 11 của cấp số nhân đã cho.
Nếu anh Nam nhận được lời mời làm việc cho một công ty nước ngoài với mức lương khởi điểm là \[35000\] đô la mỗi năm và được tăng thêm \[1400\] đô la lương mỗi năm, thì sẽ mất bao nhiêu năm làm việc để tổng lương mà anh Nam nhận được là \[319200\] đô la?
Tính giới hạn \[\lim \left[ {\frac{1}{{1.3}} + \frac{1}{{2.4}} + .... + \frac{1}{{n\left( {n + 2} \right)}}} \right]\] (viết kết quả dưới dạng số thập phân).
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình thang với \[AD\parallel BC\] và \[AD = 2BC\]. Gọi \[M\] là điểm trên cạnh \[SD\] thỏa mãn \[SM = \frac{1}{3}SD.\] Mặt phẳng \[\left( {ABM} \right)\] cắt cạnh bên \[SC\] tại điểm \[N\]. Tính tỉ số \[\frac{{SN}}{{SC}}.\]