Bộ 5 đề thi giữa kì 1 Toán 10 Chân trời sáng tạo cấu trúc mới (có tự luận) có đáp án - Đề 4
21 câu hỏi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN
A. TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Viết mệnh đề sau bằng ký hiệu\(\;\forall \) và \(\exists \): “Mọi số thực đều có bình phương không âm”.
\(\forall x \in \mathbb{R}:{x^2} \ge 0\).
\(\exists x \in \mathbb{R}:{x^2} \ge 0\).
\(\exists x \in \mathbb{R}:{x^2} \le 0\).
\(\forall x \in \mathbb{R}:{x^2} \le 0\).
Mệnh đề phủ định của mệnh đề “9 > 4” là
\(9 < 4\).
\(9 \le 4\).
\(9 \ge 4\).
\(4 < 9\).
Cho tập hợp \(A = \left\{ {x \in \mathbb{Z}| - 1 \le x \le 4} \right\}\). Tập hợp A được viết dưới dạng liệt kê các phần tử là
\(A = \left\{ { - 1;0;1;2;3} \right\}\).
\(A = \left\{ {0;1;2;3} \right\}\).
\(A = \left\{ {0;1;2;3;4} \right\}\).
\(A = \left\{ { - 1;0;1;2;3;4} \right\}\).
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
\(x - 3{y^2} \ge 0\).
\(\left( {x - 1} \right)\left( {y + 3} \right) < x + 2\).
\(2x + 3y \ge 4\).
\(x + \frac{2}{y} < 0\).
Điểm \(M\left( {2023;1} \right)\) thuộc miền nghiệm của hệ bất phương trình nào sau đây?
\(\left\{ \begin{array}{l}x + 2y \ge 3\\3x - y \le 0\end{array} \right.\).
\(\left\{ \begin{array}{l}3x + 2y \ge 2\\x - 2y < 5\end{array} \right.\).
\(\left\{ \begin{array}{l}5x + 2y \ge 1\\3x - y \le 4\end{array} \right.\).
\(\left\{ \begin{array}{l}x - 2y > 7\\ - 2x + y \le 3\end{array} \right.\).
Cho \(45^\circ < \alpha < 90^\circ \). Khẳng định nào sau đây sai?
\(\tan \alpha > 0\).
\(\sin \alpha > 0\).
\(\cos \alpha < 0\).
\(\cot \alpha > 0\).
Cho tam giác \(ABC\) có chu vi bằng 12 và bán kính đường tròn nội tiếp bằng 1. Diện tích của tam giác \(ABC\) bằng
\(12\).
\(3\).
\(6\).
\(24\).
Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương. Khẳng định nào sau đây đúng?
\(\overrightarrow a \) và \(\overrightarrow b \) có giá trùng nhau.
\(\overrightarrow a \) và \(\overrightarrow b \) có giá song song.
\(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng.
\(\overrightarrow a \) và \(\overrightarrow b \) có giá song song hoặc trùng nhau.
Cho bốn điểm phân biệt \[A,B,C,D\]. Vectơ tổng \[\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {BC} + \overrightarrow {DA} \] bằng
\(\overrightarrow 0 \).
\(\overrightarrow {AC} \).
\(\overrightarrow {BD} \).
\(\overrightarrow {BA} \).
Mệnh đề nào sau đây sai?
Nếu một tam giác có một góc bằng \(60^\circ \) thì tam giác đó là đều.
Tam giác \(ABC\) cân tại\(A\)\[ \Rightarrow \]\(AB = AC\).
Tổng của hai cạnh một tam giác lớn hơn cạnh thứ ba.
Tam giác \(ABC\) vuông tại \(C\)\[ \Rightarrow \]\(A{B^2} = C{A^2} + C{B^2}\).
Phần không bị gạch (kể cả bờ) trong hình vẽ là miền nghiệm của bất phương trình nào sau đây?
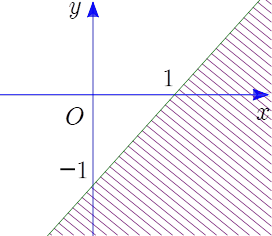
\(x - y \ge 1\).
\(x - y \le 1\).
\(x + y > 1\).
\(x + y \le 1\).
Cho biết \(\cos \alpha = - \frac{2}{3}\). Tính giá trị của biểu thức \(E = \frac{{\cot \alpha + 3\tan \alpha }}{{2\cot \alpha + \tan \alpha }}\).
\( - \frac{{19}}{{13}}\).
\(\frac{{19}}{{13}}\).
\(\frac{{25}}{{13}}\).
\( - \frac{{25}}{{13}}\).
B. TRẮC NGHIỆM ĐÚNG - SAI. Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hai tập \(A = \left\{ {x \in \mathbb{R}|x + 2 \ge 0} \right\}\) và \(B = \left\{ {x \in \mathbb{R}|2x - 1 < 0} \right\}\).
a) \(A = \left[ { - 2; + \infty } \right)\), \(B = \left( { - \infty ;\frac{1}{2}} \right)\).
b) Biểu diễn trên trục số tập hợp \(A\) là
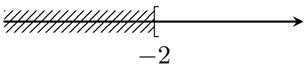
c) \(A \cap B = \left( { - \infty ; + \infty } \right)\).
d) Số phần tử nguyên của tập hợp \(A \cap B\) là 5.
Cho tam giác \(ABC\) có và \(N\) lần lượt là trung điểm của \(AB\) và \(AC\). Lấy điểm \(P\) đối xứn\(M\)g với điểm \(M\) qua \(N\).
a) \(MN = BC\).
b) \(\left| {\overrightarrow {MP} } \right| = \left| {\overrightarrow {BC} } \right|\).
c) \(\overrightarrow {MN} \) và \(\overrightarrow {BC} \) ngược hướng.
d) \(\overrightarrow {MP} = \overrightarrow {BC} \).
C. TRẢ LỜI NGẮN. Thí sinh trả lời câu 1 đến câu 4.
Một cửa hàng bán hai loại đồ uống có tên là “Giọt lệ thiên thần” và “Giọt lệ ác quỷ”. Bốn ly “Giọt lệ thiên thần” có giá \(600\,000\) đồng, ba ly “Giọt lệ ác quỷ” có giá \(540\,000\) đồng. Hàng tháng, cửa hàng này phải chi trả \(6\,000\,000\) đồng tiền thuê nhân viên, \(8\,000\,000\) đồng tiền thuê mặt bằng, \(3\,000\,000\) đồng tiền nguyên liệu. (Ngoài ra cửa hàng không tốn thêm bất kỳ chi phí gì và thu nhập của cửa hàng chỉ đến từ việc bán hai loại đồ uống trên). Gọi \[x\] và \(y\) lần lượt là số ly “Giọt lệ thiên thần” và “Giọt lệ ác quỷ” mà cửa hàng bán được trong một tháng. Điều kiện của \[x\] và \(y\) để doanh thu của cửa hàng trong một tháng có lãi thoả mãn bất phương trình \(ax + by > 1700\) với \(a,\,b \in \mathbb{N}\). Tính giá trị biểu thức \(T = 2a + b\).
Cho \(\sin x + \cos x = 0,2\). Tính giá trị của biểu thức \(P = \left| {\sin x - \cos x} \right|\).
Tỉnh \(A\) và \(B\) bị ngăn cách nhau bởi một ngọn núi. Để đi từ tỉnh \(A\) đến tỉnh \(B\), người ta đi theo lộ trình từ tỉnh \(A\) qua tỉnh \(C\), rồi đến tỉnh \(B\). Biết rằng lộ trình từ \(A\) đến \(C\) dài 70 km, từ \(C\) đến \(B\) dài 100 km, và hai con đường tạo với nhau góc \(60^\circ \). Cứ mỗi 20 km quãng đường thì phương tiện tiêu hao 1 lít nhiên liệu. Để tiết kiệm nhiên liệu, người ta làm một đường hầm xuyên núi để đi từ tỉnh \(A\) đến tỉnh \(B\). Hỏi nếu đi theo đường hầm thì phương tiện tiết kiệm được bao nhiêu lít nhiên liệu (làm tròn kết quả đến hàng phần trăm)?
Cho tam giác vuông cân tại \(A\), có cạnh \(AB\) bằng \[\sqrt 2 \]. Tính độ dài vectơ tổng \[ABC\].
Một cửa hàng dự định làm kệ sách và bàn làm việc để bán. Mỗi kệ sách cần 5 giờ chế biến gỗ và 4 giờ hoàn thiện. Mỗi bàn làm việc cần 10 giờ chế biến gỗ và 3 giờ hoàn thiện. Mỗi tháng cửa hàng có không quá 600 giờ để chế biến gỗ và không quá 240 giờ để hoàn thiện. Lợi nhuận dự kiến của mỗi kệ sách là 400 nghìn đồng và mỗi bàn làm việc là 750 nghìn đồng. Mỗi tháng cửa hàng cần làm bao nhiêu sản phẩm mỗi loại để lợi nhuận thu được là lớn nhất nếu bán hết sản phẩm làm ra?
Trên biển, tàu \(B\) ở vị trí cách tàu \(A\) \(50\)km về hướng \({\rm{N}}34^\circ {\rm{E}}\). Sau đó, tàu \(B\) chuyển động thẳng đều với vận tốc có độ lớn \(20\)km/h về hướng đông, đồng thời tàu \(A\) chuyển động thẳng đều với vận tốc có độ lớn \(30\) km/h để gặp tàu \(B\).
a) Hỏi tàu \(A\) cần phải chuyển động theo hướng nào?
b) Với hướng chuyển động đó thì sau bao lâu tàu \(A\) gặp tàu \(B\)?
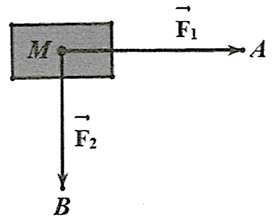
Cho hai lực \(\overrightarrow {{F_1}} = \overrightarrow {MA} ,\overrightarrow {{F_2}} = \overrightarrow {MB} \) cùng tác động vào một vật tại điểm \(M\). Cường độ hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) lần lượt là 400 N và 300 N, \(\widehat {AMB} = 90^\circ \). Tính cường độ của lực tác động lên vật.