Bộ 5 đề thi cuối kì 1 Toán 10 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 01
22 câu hỏi
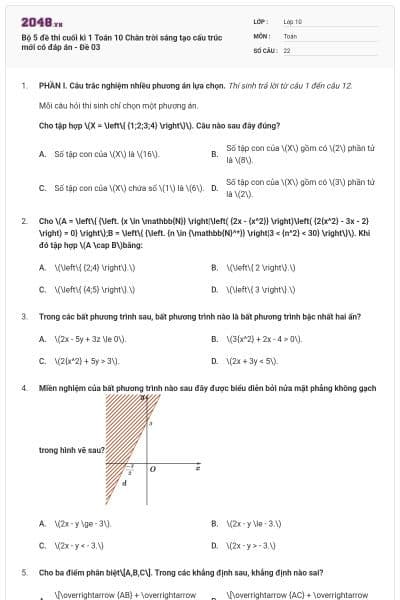
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho mệnh đề P: “ ”. Xác định mệnh đề phủ định của mệnh đề P.
.
.
.
.
Cho hai tập hợp \(A = \left\{ {1;2;3;4;5} \right\}\) và \(B = \left\{ {0;2;4;6;8} \right\}\). Tìm \(A\backslash B\).
\(A\backslash B = \left\{ {2;4} \right\}\).
\(A\backslash B = \left\{ {1;3;5} \right\}\).
\(A\backslash B = \left\{ {0;1;3;5} \right\}\).
\(A\backslash B = \left\{ {0;6;8} \right\}\).
Trong mặt phẳng \(Oxy\), điểm nào trong các điểm sau không thuộc miền nghiệm của bất phương trình \(x - 4y + 5 > 0\)?
\(\left( {2\,;\,1} \right)\).
\(\left( { - 5\,;\,0} \right)\).
\(\left( {0\,;\,0} \right)\).
\(\left( {1\,;\, - 3} \right)\).
Trong các cặp số sau, cặp nào không là nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x + y - 2 \le 0\\2x - 3y + 2 > 0\end{array} \right..\)
\(\left( {0;0} \right)\).
\(\left( {1;1} \right)\).
\(\left( { - 1;1} \right)\).
\(\left( { - 1; - 1} \right)\).
Cho ba điểm \(A,B,C\) không thẳng hàng. Số vectơ khác vectơ-không có điểm đầu và điểm cuối trùng với các điểm \(A,B,C\) là
\(3\).
\(5\).
\(6\).
\(9\).
Cho hình bình hành ABCD. Hai điểm M, N lần lượt là trung điểm của BC và AD. Tìm đẳng thức sai:
\(\overrightarrow {AM} + \overrightarrow {AN} = \overrightarrow {AC} \).
\(\overrightarrow {AM} + \overrightarrow {AN} = \overrightarrow {AB} + \overrightarrow {AD} \).
\(\overrightarrow {AM} + \overrightarrow {AN} = \overrightarrow {MC} + \overrightarrow {NC} \).
\(\overrightarrow {AM} + \overrightarrow {AN} = \overrightarrow {DB} \).
Cho tam giác \(ABC\) đều nội tiếp trong đường tròn tâm \(I\) bán kính bằng 3. Gọi \(D\) là điểm nằm trên đường tròn \(\left( I \right)\). Tính \(\left| {\overrightarrow {DA} + \overrightarrow {BD} + \overrightarrow {DC} } \right|\).
\(3\).
\(9\).
\(6\).
\(3\sqrt 2 \).
Cho tam giác đều \(ABC\) có cạnh bằng \(a.\) Tính tích vô hướng \(\overrightarrow {AB} .\overrightarrow {AC} .\)
\(\overrightarrow {AB} .\overrightarrow {AC} = 2{a^2}.\)
\(\overrightarrow {AB} .\overrightarrow {AC} = - \frac{{{a^2}\sqrt 3 }}{2}\).
\(\overrightarrow {AB} .\overrightarrow {AC} = - \frac{{{a^2}}}{2}\).
\(\overrightarrow {AB} .\overrightarrow {AC} = \frac{{{a^2}}}{2}\).
Thời gian chờ xe bus trung bình của 10 học sinh trên là.
\(8,8\) phút.
\(9\) phút.
\(9,5\) phút.
\(10\) phút.
Mốt của mẫu số liệu trên là
\(25\).
\(6\)
\(8\).
\(12\).
Giá trị ngoại lệ của mẫu số liệu trên là
\(25\).
\(6\).
\(8\).
\(12\).
Độ lệch chuẩn về thời gian chờ xe bus của 10 học sinh trên là (làm tròn kết quả đến hàng phần trăm).
\(6,07\) phút.
\(6,27\) phút.
\(6,3\) phút.
\(6,7\) phút.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Một công ty viễn thông tính phí 1 nghìn đồng mỗi phút gọi nội mạng và 2 nghìn đồng mỗi phút gọi ngoại mạng. Gọi \(x\) và \(y\) lần lượt là số phút gọi nội mạng, ngoại mạng của Bình trong một tháng và Bình muốn số tiền phải trả cho tổng đài luôn thấp hơn 100 nghìn đồng. Khi đó:
a) Số tiền phải trả cho cuộc gọi nội mạng mỗi tháng là \(x\) (nghìn đồng), số tiền phải trả cho cuộc gọi ngoại mạng mỗi tháng là \(2y\) (nghìn đồng). Điều kiện \(x \in \mathbb{N},y \in \mathbb{N}\).
b) Bất phương trình bậc nhất hai ẩn theo \(x;y\) với điều kiện \(x,y \in \mathbb{N}\) là \(x + 2y < 100\).
c) \(x = 50,y = 20\) là nghiệm của bất phương trình bậc nhất gồm hai ẩn số \(x,y\) đã cho.
d) Miền nghiệm của bất phương trình bậc nhất gồm hai ẩn số \(x,y\) đã cho là một tam giác có diện tích bằng 5000.
Cho hàm số \(y = - {x^2} + 2x - 5\). Khi đó:
a) Tập xác định: \(D = \mathbb{R}\).
b) Tọa độ đỉnh \(I\) của parabol: \(I(1; - 4)\).
c) Hàm số đã cho đồng biến trên khoảng \(\left( { - \infty ;1} \right)\) và nghịch biến trên khoảng \(\left( {1; + \infty } \right)\).
d) Giá trị lớn nhất của hàm số là \({y_{\max }} = - 4\), khi \(x = 2\).
Tam giác \(ABC\) có \(AB = 14,AC = 13,BC = 15\).
a) \(S = \sqrt {p\left( {p - 13} \right)\left( {p - 14} \right)\left( {p - 15} \right)} \) với \(p = \frac{{AB + AC + BC}}{2}\).
b) Tam giác \(ABC\) có bán kính đường tròn nội tiếp là 4.
c) Độ dài đường cao ứng với cạnh \(AB\) có độ dài là 12.
d) Tam giác \(ABC\) có 3 góc là góc nhọn.
Cho tam giác \(ABC\) có hai đường trung tuyến \(BN,CP\). Khi đó:
a) \(G\) là trọng tâm của tam giác \(ABC\), ta có : \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \vec 0\).
b) \(\overrightarrow {BA} + \overrightarrow {BC} = 3\overrightarrow {BN} \).
c) \(\overrightarrow {AB} = - \frac{2}{3} \cdot \overrightarrow {BN} - \frac{2}{3}\overrightarrow {CP} \).
d) \(\overrightarrow {BC} = - \frac{2}{3}\overrightarrow {CP} + \frac{2}{3}\overrightarrow {BN} {\rm{. }}\)
PHẦN III. Câu trắc nghiệm trả lời ngắn.Thí sinh trả lời câu 1 đến câu 6.
Một công ty dịch vụ cho thuê xe hơi vào dịp tết với giá thuê mỗi chiếc xe hơi như sau: khách thuê tối thiểu phải thuê trọn ba ngày tết (mùng 1, 2, 3) với giá 1000000 đồng/ngày; những ngày còn lại (nếu khách còn thuê) sẽ được tính giá thuê là 700000 đồng/ngày. Giả sử T là tổng số tiền mà khách phải trả khi thuê một chiếc xe hơi của công ty và \(x\) là số ngày thuê của khách. Hỏi nếu khách thuê một chiếc xe hơi công ty trong 7 ngày tết thì sẽ trả khoản tiền thuê là bao nhiêu đồng?
Cho biểu thức \(A = \frac{{4\tan x + 2\cot x}}{{\tan x + \cot x + 3}} = 2\). Tính giá trị của biểu thức \(P = \frac{{2\sin x + \cos x}}{{3\sin x - 2\cos x}}.\)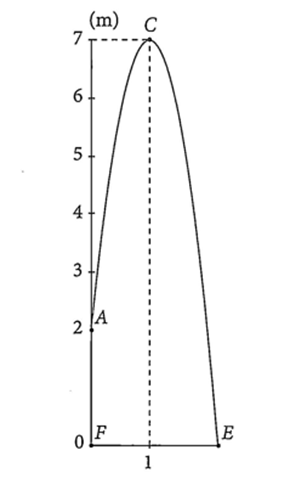
Một viên bi được ném xiên từ vị trí \(A\) cách mặt đất \(2\;{\rm{m}}\) theo quỹ đạo dạng parabol như hình vẽ sau đây. Khoảng cách từ vị trí \(E\) đến vị trí \(F\) là bao nhiêu mét, biết rằng vị trí \(E\) là nơi viên bi rơi xuống chạm mặt đất (kết quả làm tròn đến hàng phần trăm).
Để đo khoảng cách từ một điểm A trên bờ sông đến gốc cây C trên cù lao giữa sông, người ta chọn một điểm B cùng ở trên bờ với A sao cho từ A và B có thể nhìn thấy điểm C. Ta đo được khoảng cách AB = 40 m, \(\alpha = \widehat {CAB} = 45^\circ \) và \(\beta = \widehat {CBA} = 70^\circ \). Tính khoảng cách từ A đến gốc cây C trên cù lao (làm tròn đến hàng phần trăm).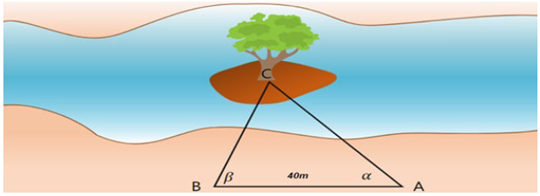
Cho ba lực \(\overrightarrow {{F_1}} = \overrightarrow {MA} ,\overrightarrow {{F_2}} = \overrightarrow {MB} ,\overrightarrow {{F_3}} = \overrightarrow {MC} \) cùng tác động vào một vật tại điểm \(M\) và vật đứng yên. Cho biết cường độ của \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) đều bằng \(100\;{\rm{N}}\) và \(\widehat {AMB} = 90^\circ \). Khi đó tính cường độ của lực \(\overrightarrow {{F_3}} \) (kết quả làm tròn đến hàng đơn vị).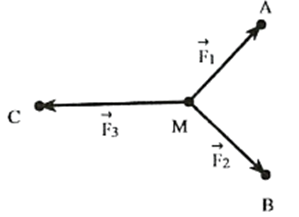
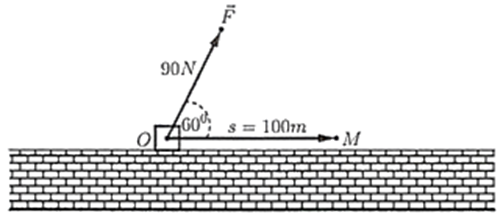
Một người dùng một lực \(\vec F\) có độ lớn \(90\;{\rm{N}}\) làm một vật dịch chuyển một đoạn \(100\;{\rm{m}}\). Biết lực \(\vec F\) hợp với hướng dịch chuyển một góc \(60^\circ \). Công sinh ra bởi lực \(\vec F\) bằng bao nhiêu Jun.